大数据HCIE成神之路之数据预处理(3)——特征缩放
1.1 标准化
标准化是将训练集中的某一列 (特征) 缩放成均值为0、方差为1的状态,该方法被广泛用于许多机器学习算法(如支持向量机、逻辑回归、人工神经网络)的归一化。
标准化的实现使用Python中preprocessing库的 scale() 函数,其基本格式如下:
sklearn.preprocessing.scale(X, axis=0, with_mean=True,with_std=True,copy=True)
关键参数详解:
- X,表示数组或矩阵。
- axis=0,int类型,默认为0。axis用来计算
均值和标准方差。若为0,则对每个观测样本(列)进行标准化,若为1,则对每个观测样本(行)进行标准化。【重点注意】 - with_mean=True,boolean类型,默认为True。表示将数据
均值规范到0。 - with_std=True,boolean类型,默认为True。表示将数据
方差规范到1。
1.1.1 实验任务
1.1.1.1 实验背景
为了数据处理更加方便,利用标准化将数据缩放成均值为0、方差为1的状态,更便捷快速。
补充阅读文章:方差、标准差、标准误、离差的联系和区别
1.1.1.2 实验目标
使用scale()函数实现数据集的标准化操作。
1.1.1.3 实验数据解析
实验数据使用鸢尾花数据集。
1.1.2 实验思路
标准化:
- 导入实验数据集。
- 使用scale()函数对实验数据集进行标准化操作。
1.1.3 实验操作步骤
步骤 1 导入数据集
#导入数据集 iris
from sklearn.datasets import load_iris
iris=load_iris()
#部分数据展示
iris
部分输出结果如下:
{'data': array([[5.1, 3.5, 1.4, 0.2],
? [4.9, 3. , 1.4, 0.2],
? [4.7, 3.2, 1.3, 0.2],
? [4.6, 3.1, 1.5, 0.2],
? [5. , 3.6, 1.4, 0.2],
? [5.4, 3.9, 1.7, 0.4],
? [4.6, 3.4, 1.4, 0.3],
? [5. , 3.4, 1.5, 0.2],
? [4.4, 2.9, 1.4, 0.2],
步骤 2 使用 scale() 函数对鸢尾花数据集进行标准化操作
# 导入数据预处理需要的类
from sklearn import preprocessing
import numpy as np
# 对鸢尾花数据集进行标准化操作
x= preprocessing.scale(iris.data)
x
输出结果如下:
array([[-9.00681170e-01, 1.03205722e+00, -1.34127240e+00,
? -1.31297673e+00],
? [-1.14301691e+00, -1.24957601e-01, -1.34127240e+00,
? -1.31297673e+00],
? [-1.38535265e+00, 3.37848329e-01, -1.39813811e+00,
? -1.31297673e+00],
? [-1.50652052e+00, 1.06445364e-01, -1.28440670e+00,
? -1.31297673e+00],
? [-1.02184904e+00, 1.26346019e+00, -1.34127240e+00,
? -1.31297673e+00],
1.1.4 结果验证
由上述实验结果可知,原先没有规律的数据经过标准化操作后,得到的输出结果都是无限趋近于零,且波动程度不大的数据。所以 scale() 函数实现了将数据缩放成均值为0,方差为1的标准化操作。
1.2 最小值-最大值归一化
最小值-最大值归一化是将训练集中原始数据中特征的取值缩放到0到1之间。这种特征缩放方法实现对原始数据的等比例缩放,比较适用于数值比较集中的情况。
最小值-最大值归一化的实现使用Python中sklearn库的 MinMaxScaler() 函数,其基本格式如下:
MinMaxScaler(feature_range=(0, 1), copy=True)
关键参数详解:
- feature_range=(0, 1),默认缩放范围为(0, 1)。也可自定义设置最大值最小值范围。
1.2.1 实验任务
1.2.1.1 实验背景
利用最小值-最大值归一化将数据映射到0~1范围之内处理,该方法实现对原始数据的等比例缩放。
1.2.1.2 实验目标
对数据集中的数据进行最小值-最大值归一化的操作。
1.2.1.3 实验数据解析
实验数据使用鸢尾花数据集。
1.2.2 实验思路
- 导入实验数据集。
- 使用
MinMaxScaler()函数对实验数据集进行最小值-最大值归一化操作。
1.2.3 实验操作步骤
步骤 1 导入数据集
#导入数据集 iris
from sklearn.datasets import load_iris
iris=load_iris()
步骤 2 最小值-最大值归一化
#导入 MinMaxScaler 类
from sklearn.preprocessing import MinMaxScaler
#对鸢尾花数据集进行最小值-最大值归一化
x=MinMaxScaler().fit_transform(iris.data)
x
部分输出结果如下:
array([[0.22222222, 0.625 , 0.06779661, 0.04166667],
? [0.16666667, 0.41666667, 0.06779661, 0.04166667],
? [0.11111111, 0.5 , 0.05084746, 0.04166667],
? [0.08333333, 0.45833333, 0.08474576, 0.04166667],
? [0.19444444, 0.66666667, 0.06779661, 0.04166667],
? [0.30555556, 0.79166667, 0.11864407, 0.125 ],
? [0.08333333, 0.58333333, 0.06779661, 0.08333333],
总结:
#标准化的关键代码:
from sklearn import preprocessing
x= preprocessing.scale(iris.data)
#最小值-最大值归一化的关键代码:
from sklearn.preprocessing import MinMaxScaler
x=MinMaxScaler().fit_transform(iris.data)
#虽然scale()和fit_transform()都有很多参数,但是最直接的就是传数据。
思考:
from sklearn.preprocessing import MinMaxScaler
x=MinMaxScaler().fit_transform(iris.data)
提问:为什么是 fit_transform ? fit_transform 在哪些地方还有用处
回答:在scikit-learn中,估计器(estimator)通常具有fit和transform方法。fit方法用于根据数据 拟合 模型的参数,而transform方法用于根据已经拟合的模型对数据进行 转换 。fit_transform方法则结合了这两个步骤,先拟合模型参数,然后对数据进行转换。
具体地说,在这个例子中,MinMaxScaler是一个用于特征缩放的估计器。fit_transform方法首先使用fit方法根据数据计算出最小值和最大值,然后使用这些最小值和最大值对数据进行归一化转换,将特征缩放到[0, 1]的范围内。
fit_transform方法在其他预处理和特征工程技术中也经常使用。例如,在 PCA (主成分分析)中,fit_transform方法用于拟合数据并进行降维转换。在 文本处理 中,fit_transform方法用于学习词汇表并将文本转换为向量表示。在 特征选择 中,fit_transform方法用于计算特征的相关性或重要性,并选择最相关的特征子集。
注意:feature_range=(0, 1)参数是写在MinMaxScaler()中。
1.2.4 结果验证
由上述实验结果可知,原先没有规律的数据经过最大值-最小值归一化操作后,得到的输出结果都是在0~1的范围内的。所以 MinMaxScaler() 函数实现了将数据映射到0~1范围之内的功能。
1.3 均值归一化
均值归一化也是特征缩放中一种常见的方法,是用来减小样本数据的波动使得梯度下降地更快,从而达到全局最小值。由于Python中没有直接调用的函数来实现均值归一化,所以下面将采用公式计算实现对数据集的均值归一化操作。公式如下:
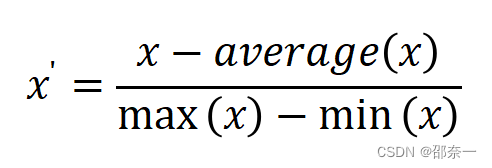
1.3.1 实验任务
1.3.1.1 实验背景
利用 均值归一化 将数据转换为 无量纲化指标测评值 ,即各指标值都处于同一个数量级别上,为后期的分析等流程提供帮助。
1.3.1.2 实验目标
对数据集中的数据进行均值归一化的操作。
1.3.2 实验思路
- 导入实验数据集。
- 按照均值归一化的公式计算数据集的均值归一化。
1.3.3 实验操作步骤
步骤 1 导入数据集
iris是150*4的数据集,为实验过程更易被理解。特取其中一个属性进行均值归一化实验。本实验选取数据集中的第一维 sepal length (cm) 。
from sklearn.datasets import load_iris
iris=load_iris()
x=iris.data[:,1]
x
输出结果如下:
#部分关键数据展示
array([3.5, 3. , 3.2, 3.1, 3.6, 3.9, 3.4, 3.4, 2.9, 3.1, 3.7, 3.4, 3. ,
? 3. , 4. , 4.4, 3.9, 3.5, 3.8, 3.8, 3.4, 3.7, 3.6, 3.3, 3.4, 3. ,
? 3.4, 3.5, 3.4, 3.2, 3.1, 3.4, 4.1, 4.2, 3.1, 3.2, 3.5, 3.1, 3. ,
? 3.4, 3.5, 2.3, 3.2, 3.5, 3.8, 3. , 3.8, 3.2, 3.7, 3.3, 3.2, 3.2,
? 3.1, 2.3, 2.8, 2.8, 3.3, 2.4, 2.9, 2.7, 2. , 3. , 2.2, 2.9, 2.9,
? 3.1, 3. , 2.7, 2.2, 2.5, 3.2, 2.8, 2.5, 2.8, 2.9, 3. , 2.8, 3. ,
步骤 2 计算数据集的平均值,最大值,最小值
#导入 numpy 库,计算平均值,最大值,最小值
import numpy as np
mean=np.mean(x)
min=np.min(x)
max=np.max(x)
步骤 3 根据均值归一化的公式计算数据集的均值归一化
#计算数据集均值归一化
MeanNormalization=(x-mean)/(max-min)
#输出结果
MeanNormalization
部分输出结果如下:
array([ 0.18444444, -0.02388889, 0.05944444, 0.01777778, 0.22611111,
0.35111111, 0.14277778, 0.14277778, -0.06555556, 0.01777778,
0.26777778, 0.14277778, -0.02388889, -0.02388889, 0.39277778,
0.55944444, 0.35111111, 0.18444444, 0.30944444, 0.30944444,
0.14277778, 0.26777778, 0.22611111, 0.10111111, 0.14277778,
-0.02388889, 0.14277778, 0.18444444, 0.14277778, 0.05944444,
0.01777778, 0.14277778, 0.43444444, 0.47611111, 0.01777778,
0.05944444, 0.18444444, 0.22611111, -0.02388889, 0.14277778,
0.18444444, -0.31555556, 0.05944444, 0.18444444, 0.30944444
1.3.4 结果验证
由于结果显示为数据显示,所以无法直接看出均值归一化对后期优化算法的作用。但如果采用二维或三维的坐标系将结果展示出来就会看出经过均值归一化操作后,原始数据均转换为无量纲化指标测评值,即各指标值都处于同一个数量级别上,为后期数据分析提供了帮助。
1.4 缩放成单位向量
缩放成单位向量的过程是将每个样本缩放到单位范数(每个样本的范数为1),有利于对后续计算两个样本之间的相似性。
缩放成单位向量的实现需要先使用Python中linalg库的 norm() 函数来求数据的欧几里得距离,其基本格式如下:
norm(x, ord=None, axis=None, keepdims=False)
关键参数详解:
- x,表示数组或矩阵。
- ord=None,表示范数的类型,默认为二范数。若为1,则是一范数;若为2,则是二范数;若为np.inf,则是无穷范数。
- axis=None,表示处理的类型。若为1,则表示按
行向量处理,求多个行向量的范数;若为0则表示按列向量处理,求多个列向量的范数;若为None,则表示矩阵范数。【重点注意】 - keepdims=False,表示是否保持矩阵的二维特性。若为Ture,则表示保持矩阵的二维特性,False相反。
1.4.1 实验任务
1.4.1.1 实验背景
利用 均值归一化 将数据转换为无量纲化指标测评值,即各指标值都处于同一个数量级别上,为后期的分析等流程提供帮助。
1.4.1.2 实验目标
对数据集中的数据进行缩放成单位向量的操作。
1.4.1.3 实验数据解析
实验数据使用鸢尾花数据集。
1.4.2 实验思路
缩放成单位向量:
- 导入实验数据集。
- 将数据的欧几里得距离计算出来。
- 根据缩放成单位向量的公式计算。
1.4.3 实验操作步骤
步骤 1 导入数据集
iris是150*4的数据集,为实验过程更易被理解。特取其中一个属性进行均值归一化实验。本实验选取数据集中的第二维sepal width (cm)。
from sklearn.datasets import load_iris
iris=load_iris()
x=iris.data[:,1]
x
步骤 2 计算数据的欧几里得距离
# 导入 numpy 库,计算数据的欧几里得距离
import numpy as np
linalg = np.linalg.norm(x, ord=1)
linalg
输出结果如下:
458.6
步骤 3 根据公式将数据集缩放成单位向量
# 计算数据集的缩放成单位向量
X=x/linalg
X
输出结果:
array([0.00763192, 0.00654165, 0.00697776, 0.0067597 , 0.00784998,
0.00850414, 0.00741387, 0.00741387, 0.00632359, 0.0067597 ,
0.00806803, 0.00741387, 0.00654165, 0.00654165, 0.0087222 ,
0.00959442, 0.00850414, 0.00763192, 0.00828609, 0.00828609,
0.00741387, 0.00806803, 0.00784998, 0.00719581, 0.00741387,
0.00654165, 0.00741387, 0.00763192, 0.00741387, 0.00697776,
0.0067597 , 0.00741387, 0.00894025, 0.00915831, 0.0067597 ,
0.00697776, 0.00763192, 0.00784998, 0.00654165, 0.00741387,
0.00763192, 0.00501526, 0.00697776, 0.00763192, 0.00828609,
1.4.4 结果验证
由上述实验结果可知,原先没有规律的数据经过缩放成单位向量操作后,将每个样本缩放到单位范数。
1.5 总结
当涉及到特征缩放的选择时,我们需要考虑数据的特点以及所使用的机器学习算法。
标准化 可以消除特征之间的量纲差异,使得数据更易于比较和分析。标准化适用于大多数机器学习算法,特别是那些依赖于距离度量的算法,如支持向量机(SVM)和K近邻(KNN)算法。
最小值-最大值归一化 是另一种常见的特征缩放方式,它将特征缩放到一个指定的范围(通常是0到1之间)。这种缩放方式可以保留原始数据的分布形状和结构。最小值-最大值归一化适用于一些对原始数据的具体取值范围有要求的算法,如神经网络(Neural Networks)和图像处理算法。
均值归一化 是一种类似于标准化的特征缩放方式,但它将特征缩放到均值为0,范围在-1到1之间。均值归一化可以用于类似于标准化的应用场景,但有时候它可以更好地处理有离群值存在的数据集。
缩放成单位向量 是一种特征缩放方式,它将特征向量缩放到单位长度。具体而言,对于每个样本,特征向量的范数(即长度)将为1。这种缩放方式可以保留原始数据的方向信息。缩放成单位向量常用于文本分类等自然语言处理任务中,以及其他需要计算向量相似性的应用中。
在实际工作中,选择合适的缩放方式取决于数据的特性和所采用的机器学习算法。一般来说,标准化(Standardization)和最小值-最大值归一化(Min-Max Scaling)是最常用的特征缩放方式。
如果你的数据集中特征的分布近似为正态分布,或者你使用的机器学习算法对特征的分布不敏感,那么标准化是一个不错的选择。例如,假设你正在使用支持向量机(SVM)进行分类任务,你可以对特征进行标准化,以便使得各个特征对模型的贡献相对均衡。
如果你的数据集中特征的取值范围有界,并且你想要保留原始数据的分布形状和结构,那么最小值-最大值归一化是一个合适的选择。例如,如果你正在进行图像处理任务,你可以将图像像素的取值范围缩放到0到1之间,以便进行后续处理。
对于均值归一化(Mean Normalization)和缩放成单位向量(Scaling to Unit Vector),它们在一些特定的场景下有用。均值归一化通常用于处理有离群值存在的数据集,因为它可以在保持分布形状的同时,减少离群值对模型的影响。缩放成单位向量常用于处理文本数据或计算向量相似性的任务。
总之,选择合适的特征缩放方式需要综合考虑数据的特性、算法的要求以及具体任务的需求。在实际应用中,可以尝试不同的缩放方式,并根据模型的性能和结果进行评估,选择适合的方式。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!