相机标定张正友、opencv和halcon对比(1)
本文将从基本标定开始,结合实际工作经验,分析张正友、opencv和halcon三者相机标定的深层原理与不同之处,内容比较多,如果出现错误请指正。
相机光学模型
我们使用的镜头都是由多组镜片组成,它实际上是一种厚透镜模型,但是目前所有的相机标定是基于针孔模型来进行标定的,因此在学习标定之前,首先我们要对相机进行建模,这样能从整体上把握坐标系之间的变换关系。当然鱼眼镜头和沙姆镜头需要基于针孔模型进行二次建模,这里不细说了,有想交流的可以私信我。我们的目标就是把厚透镜模型变为针孔模型进行后续的处理。
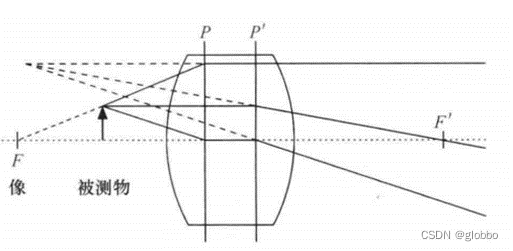
厚透镜镜片组可能如下(halcon):
针孔模型
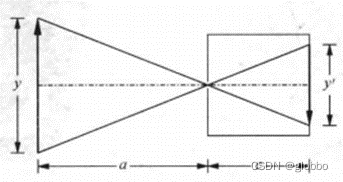
针孔模型如下图所示,小孔处为投影中心,y为物体,y’为倒立的像,a为物距,c为像距,注意这里像距并不等同于镜片的焦距,但我们一般叫焦距。
针孔模型满足下面的相似三角形关系:
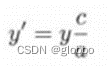
在使用中,一般我们会在投影中心o前方构造虚拟像平面,把像平面和物平面放到同一侧,这样可以使图像坐标系和相机坐标系递增方向对齐:
厚透镜模型
可以将镜头看作是两个球心位于同一直线的折射球面组成,两个球面之间为一种均匀介质,镜头两侧为另一种介质,镜头具有一定厚度,如下图所示:
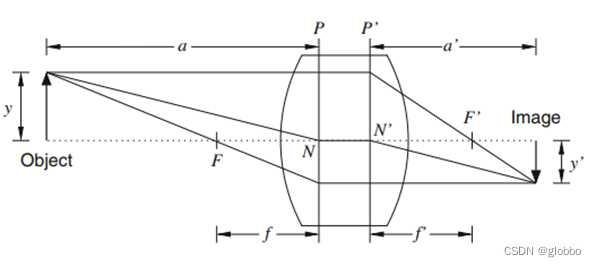
注意光是从左往右传播的,镜头前面的距离为负,向上为正,向下为负,比如y为正,y’为负,f为负,f’为正。
参数解释如下:
y 物高
y’ 像高
F 物方焦点,像方平行光线过镜头后汇聚在该点
F’ 像方焦点,物方平行光线过镜头后汇聚在该点
f 物方焦距
f’ 像方焦距,两侧介质一样的话,f等于-f’
P 物方主平面,为过像方水平光线与过F的对应光线的交点
P’ 像方主平面,为过物方水平光线与过F’的对应光线的交点
a 物距,为物到物方主平面距离
a’ 像距
N 为物方主平面与光轴交点
N’ 为像方主平面与光轴交点,入射和出射光线角度相同
这里因为有两个主平面,导致直接基于厚透镜是无法建模的。
厚透镜成像法则:
- 镜头前平行于光轴的光线,经过F’;
- 经过F的光线,通过镜头后和光轴水平;
- 过N点的光线,也会过N’点,并且镜头前和镜头后与光轴的夹角不变。
两个关键的公式:
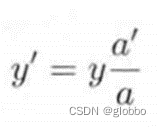
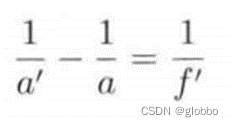
这两个公式非常关键,在做相机镜头选型时一定会用到这个公式去推断视野和成像芯片尺寸对镜头型号的影响。
可推导出如下变化:
? 物距变小,像距变大,物距变大,像距变小。也就是说,相机固定不动,焦距不变的情况下,聚焦过程其实为改变像距的过程;
? 物距无穷远,所有入射光线为平行光,此时a’=f’,像面位于像方焦点上。
? 【放大镜虚像】当物放到F点位置,像面会在无穷远处,如果物放到F以内,光线在成像端发散,a’的正负号会发生变化,像变为物体同一侧的虚像:
厚透镜转针孔模型(halcon)
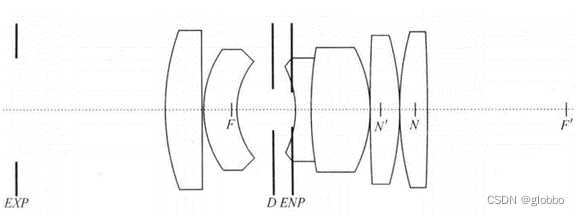
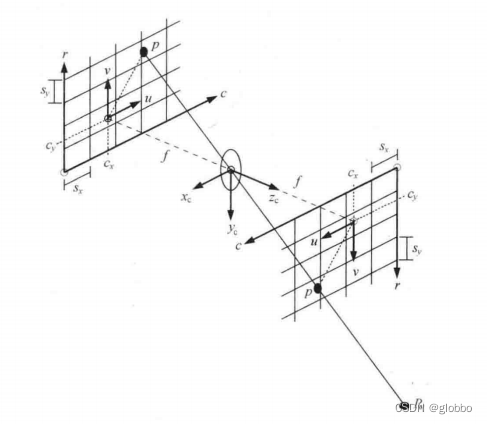
那么厚透镜到底怎么转为针孔模型呢?这里基于现有资料,这里以halcon为例进行说明。在说明之前我们必须先了解镜头中的两个概念:出瞳和入瞳。
孔径光阑和出瞳入瞳
镜头中都设计有一个可调节大小的环,来控制入射光线的多少。如下图中的D面即为环,同时镜筒本身也会限制到达像平面的光线总量,这些因素统称为光阑,其中起最大程度限制作用的被称为孔径光阑。需要注意的是,并不是最小尺寸的光阑为孔径光阑,因为光在穿过镜筒时,光阑前后的镜片可能放大或缩小光阑的实际尺寸。
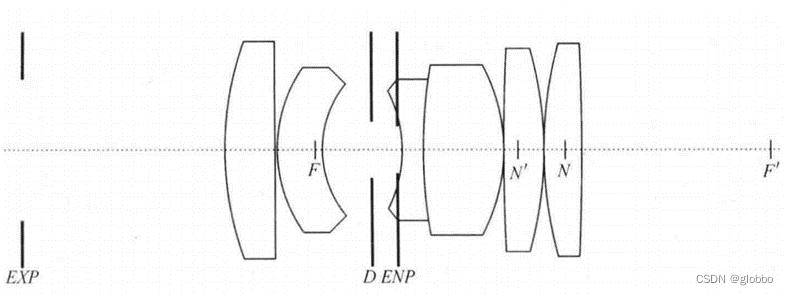
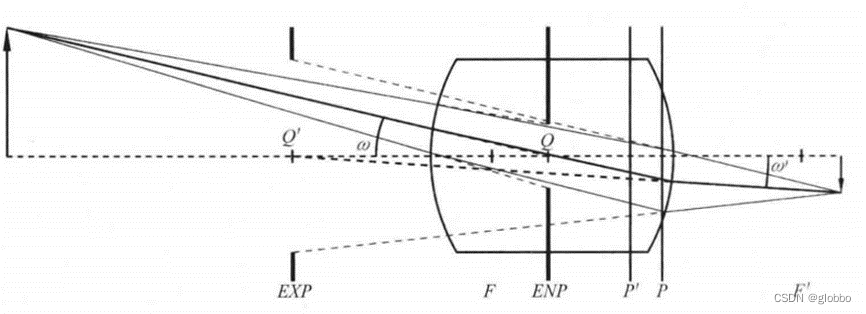
基于孔径光阑,定义了两个重要的虚拟光阑:入瞳(ENP)和出瞳(EXP)。入瞳决定镜头入口可接收的光线面积,是孔径光阑被其前面的光学系统在物方所成的像,通常为虚像。出瞳是孔径光阑被后面的光学系统在像方所成的像,通常为虚像。
主入射光线经过入瞳ENP中心Q,在主平面交点的反向延长线经过出瞳EXP中心Q’,如下图,这里入射角w和出射角w’也是不一样的:
模型转换
针孔模型中只有一个投影中心,但厚透镜模型中有两个,分别是入瞳和出瞳,同时两个角度w和w’也是不一样的,为了两个w角度一致,且物方w角度不变(因为它取决于物方被测物体的尺寸),我们只能将出瞳移动到入瞳位置(Q’移动到Q上),此时w和w’角度一致。同时我们还需要将像平面虚拟的移动到与入瞳中心距离为c的位置,来保证像平面大小不变。c为主距,也就是halcon相机标定时输入的焦距f,注意这里的主距和f’不相同。
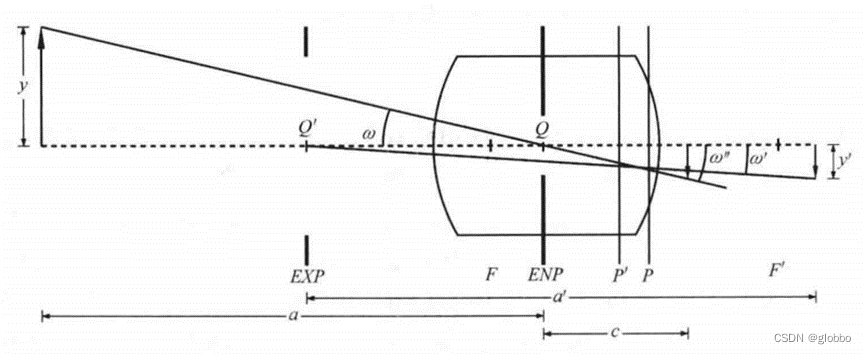
出瞳移动到入瞳,像平面移动到虚拟像平面的示意图:
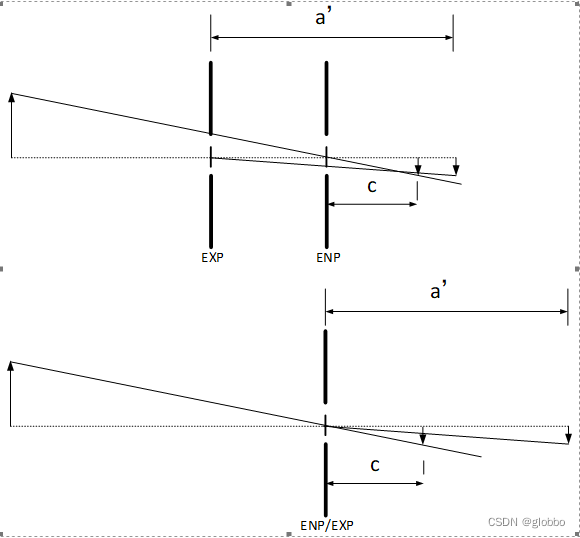
此时,厚透镜模型变转换为了由虚拟像平面、投影中心和物平面构成的针孔模型,影响最关键的参数其实是主距c。
移动后满足下面的等式:
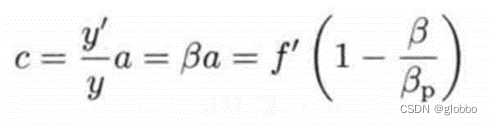
总结
说了这么多到底有什么用呢,对于普通镜头,我们可以了解到标定出的焦距其实是主距。而对于其他镜头,我认为关键是初始值的选取,尤其是沙姆标定中,我们可以基于镜头参数,推导出理论初始值进行标定,然后控制标定的结果在理想的范围内是非常关键的。
注意这里用的是halcon中的模型转换,opencv中的并没有说明它的模型怎么定义的,但我们用halcon的模型去套用应该也是没问题的。
坐标系转换
接下来是喜闻乐见的坐标系转换了,相信大家都从其他地方也看过很多,这里总结一下容易混淆及懵逼的几个点。
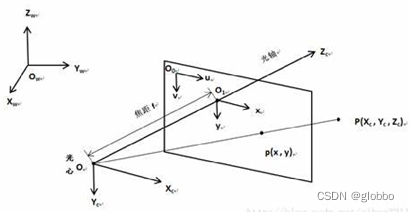
首先列一下坐标系图:
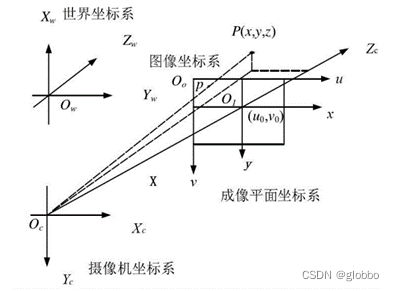
在这里包含了下面几个坐标系:
- 图像坐标系 O 0 u v O_{0}uv O0?uv,就是我们在屏幕看到的图像,它有一个中心点一般在左上角(0,0),单位是像素;
- 成像坐标系 O 1 u v O_{1}uv O1?uv,在CMOS平面内,它的中心点是光轴和CMOS平面交点,是通过像元长度计算出单位为mm或m的坐标系;
- 相机坐标系 O 1 X c Y c Z c O_{1}X_{c}Y_{c}Z_{c} O1?Xc?Yc?Zc?,它的中心即是投影中心,Zc和光轴重合,Xc和Yc和成像坐标系x轴y轴平行,单位也是mm或m;
- 世界坐标系 O w X w Y w Z w O_{w}X_{w}Y_{w}Z_{w} Ow?Xw?Yw?Zw?,它的中心即某个标定板确定的中心,单位也是mm或m。
- 针孔模型中,要求物点、投影中心和像点必须在同一条直线上。
下面开始公式推导,首先假设成像坐标系原点 O 1 O_{1} O1?在图像坐标系中的坐标为 ( u 0 , v 0 ) (u0,v0) (u0,v0),像元物理尺寸为 S x , S y S_{x},S_{y} Sx?,Sy?,镜头焦距(其实是主距)为 f f f,在图像坐标系中取一点 ( u , v ) (u,v) (u,v)。
-
图像坐标系–>成像坐标系
图像坐标系点 u , v {u,v} u,v,成像坐标系点 ( x , y ) (x,y) (x,y)
[ u v 1 ] = [ 1 S x 0 u 0 0 1 S y v 0 0 0 1 ] [ x y 1 ] \begin{bmatrix}u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{S_{x}} & 0 & u_{0}\\ 0 & \frac{1}{S_{y}} & v_{0}\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}x \\ y \\ 1 \end{bmatrix} ?uv1? ?= ?Sx?1?00?0Sy?1?0?u0?v0?1? ? ?xy1? ? (1) -
成像坐标系 – > 相机坐标系【容易理解错】
注意,这里的变换是透视投影变换,针对的是两个实际点转到相机坐标系中的变换:
一个是成像坐标系中,CMOS表面的物理点 ,转到相机坐标系中即 ( x , y , f ) (x,y,f) (x,y,f);
一个是世界坐标系中,物体表面对应的物理点,在相机坐标系中即 ( X c Y c Z c ) (X_{c}Y_{c}Z_{c}) (Xc?Yc?Zc?);
目标是将前者转到后者,因为成像坐标系中心和相机坐标系中都在光轴上,可以将该投影变换看成相似三角形的转换:
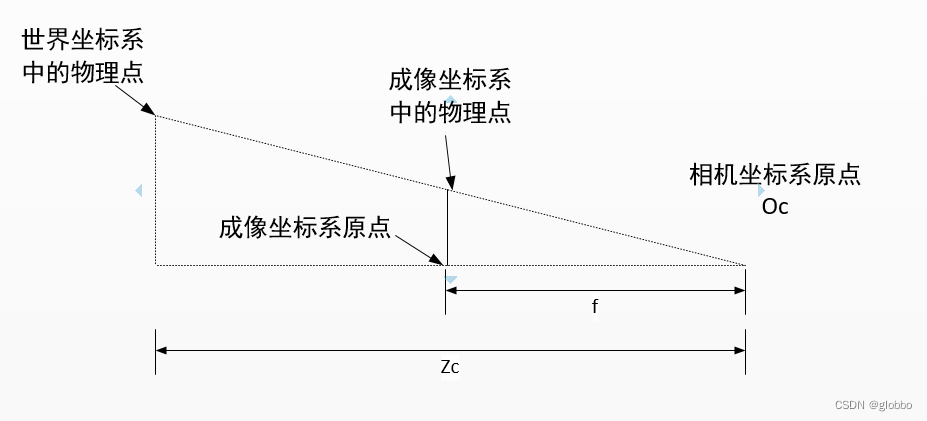
转换公式如下:
(
Z
c
[
x
y
1
]
=
[
f
0
0
0
0
f
0
0
0
0
0
1
]
[
X
c
Y
c
Z
c
1
]
)
( Z_{c}\begin{bmatrix}x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}X_{c} \\ Y_{c} \\ Z_{c} \\ 1 \end{bmatrix} )
(Zc?
?xy1?
?=
?f00?0f0?000?001?
?
?Xc?Yc?Zc?1?
?) (2)
这里的
Z
c
Z_{c}
Zc?我们一般称为尺度因子,反正最后会被约掉。
- 相机坐标系 --> 世界坐标系
这个变换是说世界坐标中的物理点,从相机坐标转到世界坐标系中,是一个旋转平移的变换:
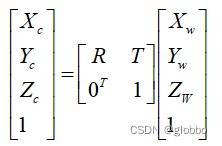
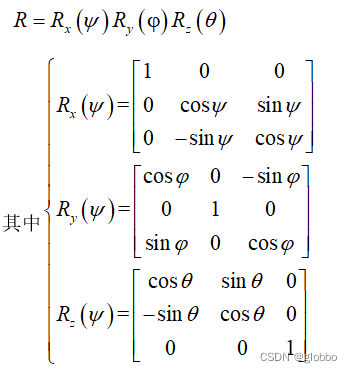
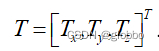
综上,整体的变换关系如下:
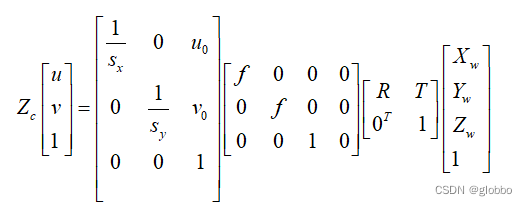
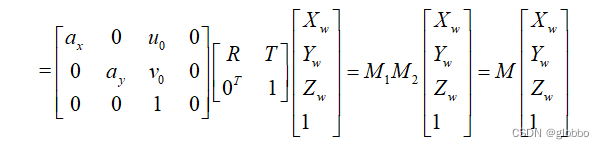
这里
M
1
M_{1}
M1?为内参矩阵,
M
2
M_{2}
M2?为平移旋转矩阵,即我们说的外参,
Z
c
Z_{c}
Zc?可以计算中自动消除。
而这,正是张正友算法的求解核心原理:利用每组的像素坐标和世界坐标,求出射影变换矩阵
M
M
M,再分别求出内参和外参的初始值,进行非线性迭代优化。
.
[
u
v
1
]
=
M
[
X
w
Y
w
Z
w
1
]
.
.\begin{bmatrix}u \\ v \\ 1 \end{bmatrix} = M \begin{bmatrix}X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} .
.
?uv1?
?=M
?Xw?Yw?Zw?1?
?.
镜头畸变对比
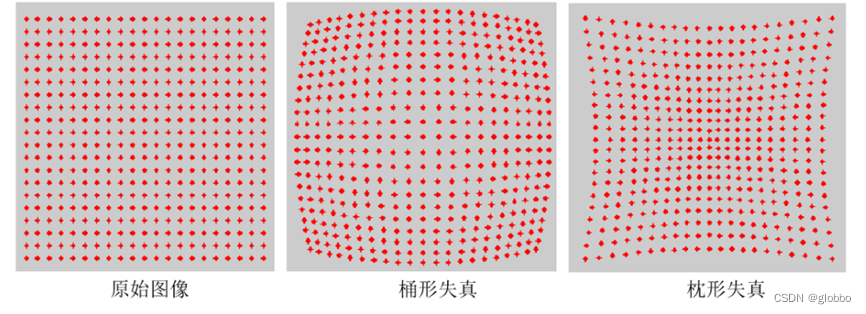
镜头畸变包含了径向畸变和切向畸变,径向畸变主要由透镜产生,它的效应主要有两种:枕形和桶形,如图所示。在 CMOS 中心(光学中心)的畸变为 0,随着向边 缘移动,畸变越来越严重。切向畸变来自于透镜安装的整个过程,因为安装时很难保证透镜和成像平面平行。
具体的公式halcon采用的和张正友是一样的:
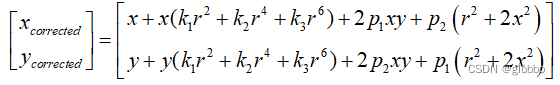
而Opencv最新版本的公式如下:
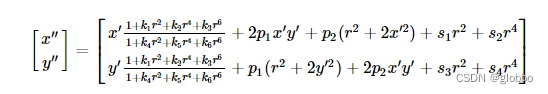
可以看到,右边径向畸变系数k,halcon和OpenCV是不一样的,但形式一致,切向是相同的,并且OpenCV还多了
(
s
1
s
2
s
3
s
4
)
(s_{1}s_{2}s_{3}s_{4})
(s1?s2?s3?s4?)四个参数。
经过对比验证,最关键的还不是这个,而是左右描述的畸变矫正不一致! 经过查询相关资料,
halcon中的公式等号右边是畸变点,等号左边是未畸变点,而张正友和OpenCV的正好相反。
这个不同点最终的影响不得而知,有谁知道的可以评论一下。
这个不同会导致一个问题,就是解畸变halcon和Opencv的过程是不一样的,halcon解畸变会更加简单,因为等号右边就是畸变的点,可以直接代入求解,但Opencv不是,它解畸变已知的是左边,求的是右边无畸变点,这个二元多次方程到底该怎么解呢?Opencv给出了一个解法。
Opencv解畸变
在 OpenCV 中,解畸变的函数主要包括 cv::undistort 和 cv::undistortPoints,我们这里看一下cv::undistortPoints函数,它里面最关键的是下面这段代码,两个for循环。
//遍历每个点
for( int i = 0; i < n; i++ )
{
double x, y, x0 = 0, y0 = 0, u, v;
u = x; v = y;
x = (x - cx)*ifx;
y = (y - cy)*ify;
if( _distCoeffs ) {
// compensate tilt distortion
cv::Vec3d vecUntilt = invMatTilt * cv::Vec3d(x, y, 1);
double invProj = vecUntilt(2) ? 1./vecUntilt(2) : 1;
x0 = x = invProj * vecUntilt(0);
y0 = y = invProj * vecUntilt(1);
double error = std::numeric_limits<double>::max();
// compensate distortion iteratively
//核心:迭代计算畸变点
for( int j = 0; ; j++ )
{
if ((criteria.type & cv::TermCriteria::COUNT) && j >= criteria.maxCount)
break;
if ((criteria.type & cv::TermCriteria::EPS) && error < criteria.epsilon)
break;
double r2 = x*x + y*y;
//下面这个是公式中的倒数
double icdist = (1 + ((k[7]*r2 + k[6])*r2 + k[5])*r2)/(1 + ((k[4]*r2 + k[1])*r2 + k[0])*r2);
if (icdist < 0) // test: undistortPoints.regression_14583
{
x = (u - cx)*ifx;
y = (v - cy)*ify;
break;
}
double deltaX = 2*k[2]*x*y + k[3]*(r2 + 2*x*x)+ k[8]*r2+k[9]*r2*r2;
double deltaY = k[2]*(r2 + 2*y*y) + 2*k[3]*x*y+ k[10]*r2+k[11]*r2*r2;
x = (x0 - deltaX)*icdist;
y = (y0 - deltaY)*icdist;
//解出来后再反向带回去,比较一下误差大小
if(criteria.type & cv::TermCriteria::EPS)
{
double r4, r6, a1, a2, a3, cdist, icdist2;
double xd, yd, xd0, yd0;
cv::Vec3d vecTilt;
r2 = x*x + y*y;
r4 = r2*r2;
r6 = r4*r2;
a1 = 2*x*y;
a2 = r2 + 2*x*x;
a3 = r2 + 2*y*y;
cdist = 1 + k[0]*r2 + k[1]*r4 + k[4]*r6;
icdist2 = 1./(1 + k[5]*r2 + k[6]*r4 + k[7]*r6);
xd0 = x*cdist*icdist2 + k[2]*a1 + k[3]*a2 + k[8]*r2+k[9]*r4;
yd0 = y*cdist*icdist2 + k[2]*a3 + k[3]*a1 + k[10]*r2+k[11]*r4;
vecTilt = matTilt*cv::Vec3d(xd0, yd0, 1);
invProj = vecTilt(2) ? 1./vecTilt(2) : 1;
xd = invProj * vecTilt(0);
yd = invProj * vecTilt(1);
double x_proj = xd*fx + cx;
double y_proj = yd*fy + cy;
error = sqrt( pow(x_proj - u, 2) + pow(y_proj - v, 2) );
}
}
}
关于这个公式,右边是无畸变的,现在已知的是左侧带畸变的
x
′
′
x^{''}
x′′,右边无畸变的
x
′
x^{'}
x′看上去是不好求的。
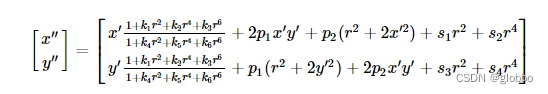
opencv使用的是不动点迭代求解非线性方程的根(参考https://blog.csdn.net/weixin_43956164/article/details/124197614),先在最里面的for中,将已知的带畸变的强行代入公式右边,注意设第一个
x
′
x^{'}
x′是未知的,这样就变成了:
(
x
′
′
?
2
p
1
x
′
′
y
′
′
?
p
2
(
r
2
+
2
x
′
2
)
?
s
1
r
2
?
s
2
r
4
1
+
k
1
r
2
+
.
.
.
1
+
k
4
r
2
+
.
.
.
=
x
′
)
(\frac{x^{''} - 2p_{1}x^{''}y^{''}-p_{2}(r^{2}+2x^{'2}) - s_{1}r^{2} - s_{2}r^{4}}{\frac{1+k_{1}r^{2}+...}{1+k_{4}r^{2}+...}}=x^{'} )
(1+k4?r2+...1+k1?r2+...?x′′?2p1?x′′y′′?p2?(r2+2x′2)?s1?r2?s2?r4?=x′)
求出来的结果,再按
x
′
x^{'}
x′和
y
′
y^{'}
y′代入公式右侧,重新得到畸变的
x
′
′
x^{''}
x′′和
y
′
′
y^{''}
y′′,然后和输入的已知进行误差求解,满足误差范围则停止。
初始值设定对比
初始值的设定是很关键的,尤其在复杂的相机模型中比如沙姆模型。这里列一下opencv和张正友标定在初始值设置时的不同:
- 张正友
整个过程参考链接:https://zhuanlan.zhihu.com/p/94244568?ivk_sa=1024320u
核心就是下面三个步骤:
1)、求解内参矩阵与外参矩阵的积;
2)、求解内参矩阵;
3)、求解外参矩阵;
4)、标定畸变系数。
-
opencv
opencv可以通过传入标记CALIB_USE_INTRINSIC_GUESS来手动控制内参和畸变的初始参数,如果不设置该标记,那么opencv会通过cvInitIntrinsicParams2D计算内参中的焦距(其中的中心位置在该函数中强行设置为了图像中心!),然后根据内参调用cvFindExtrinsicCameraParams2来计算外参,这里全局一个内参矩阵,每个图像对应一个外参,具体的方法参考的张正友但又有不同。可以参考下面两个链接,讲的很详细:
https://blog.csdn.net/weixin_43956164/article/details/127408933
https://blog.csdn.net/weixin_43956164/article/details/126771627 -
总结
张正友内参是计算得出的,opencv可以传入初始内参,也可以进行估算,两个不同点在于:
a.opencv把中心点强行设为了图像坐标系中心,而zhang是放到内参中统一估算的;
b.opencv由于强行让内参的中心点设置为了已知量,所以化简的出了一个ax=b的矩阵,动用cvSolve去解得方程,而zhang更通用,中心点也是求出的,得出一个ax=0的矩阵方程,可以动用svd分解a矩阵,得到UWV,则V矩阵的最后一列即为ax=0的解。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!