Ridge & Lasso Regression解决线性回归的过拟合(Overfitting)(基于波士顿房价预测)
目录
4、 Lasso regression 和?Ridge regression一定优于LinearRegression吗
四、Ridge?Regression和Lasso Regression
介绍:
1、过拟合
过拟合(Overfitting)是指机器学习模型过于复杂,过于精确地适应了训练数据,导致在新数据上的预测表现不佳的现象。
当一个模型过拟合时,它会在训练数据上表现得非常好,但在测试数据或新数据上的表现则很差。过拟合通常发生在模型复杂度较高、参数较多的情况下。原因可能是模型过多地记住了训练数据的细节和噪声,而忽略了数据的一般特征和模式。过拟合也可能是由于训练数据不足或不平衡导致的。
?2、Lasso regression
Lasso regression也是一种线性回归,Lasso回归也被称为L1正则化线性回归。它是线性回归的一种变体,旨在通过添加一个L1正则化项来约束模型的系数。这个正则化项可以使得某些特征的系数变为零,从而实现特征选择的效果。与岭回归(Ridge Regression)相比,Lasso回归具有更强的稀疏性,即更容易使得某些特征的系数为零。
3、?Ridge regression
?Ridge regression也是一种线性回归,岭回归(Ridge regression)是一种线性回归模型的改进方法。它通过在线性回归模型中添加一个正则化项,来解决数据特征之间共线性(多重共线性)的问题。岭回归的目标是找到最佳的回归系数,使得模型的预测误差最小化。与普通最小二乘法不同,岭回归可以对回归系数进行缩减,从而降低模型的复杂度。通过控制一个超参数λ(lambda),可以调节回归系数的惩罚力度,进而得到更合理的模型。
4、 Lasso regression 和?Ridge regression一定优于LinearRegression吗
不一定。Lasso回归和线性回归是两种不同的回归算法,适用于不同的数据情况。
Lasso回归通过加入L1正则化项,可以进行特征选择,将一些不重要的特征的系数收缩为零,从而降低模型的复杂度。这对于具有大量特征的数据集来说很有优势,可以避免过拟合,提高模型的泛化能力。然而,在某些情况下,过强的正则化可能导致模型欠拟合。
线性回归是最基本的回归算法,它假设自变量和因变量之间存在线性关系,并且不存在特征的选择问题。线性回归在数据集较小、特征较少的情况下通常表现良好,但在高维数据集和存在多重共线性的情况下可能会有问题。
不一定。Ridge回归和线性回归(Linear Regression)是两种不同的回归模型。
Ridge回归是一种正则化线性回归模型,通过在损失函数中添加一个正则化项(L2范数)来惩罚模型的复杂度,防止过拟合。Ridge回归可以有效地降低特征的影响力,避免产生过高的权重,从而提高模型的泛化能力。
而线性回归(Linear Regression)是一种最小二乘法的回归模型,通过使预测值和实际值之间的方差最小化来拟合数据。线性回归没有正则化项,模型的复杂度较低。
在某些情况下,Ridge回归可能比线性回归更好,特别是在存在多重共线性(multicollinearity)问题时。多重共线性会导致线性回归的系数估计不稳定,而Ridge回归可以通过正则化来减少这种不稳定性。
但是,在没有多重共线性问题的情况下,如果数据的特征之间关系简单且线性,线性回归可能效果更好。因为Ridge回归在惩罚模型复杂度的同时,也会降低特征的影响力,可能导致欠拟合。
因此,选择使用哪种回归模型取决于数据的特点和建模的目标。
在选择回归算法时,应该根据具体的数据情况和问题需求来决定使用哪种模型。?
X#自变量?
y#因变量
一、?Linear Regression
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
linregrassor=LinearRegression()
cvscore=cross_val_score(linregrassor,X,y,cv=5)#cv表示分成五份,一份测试集,四份训练集(五次评分)
cvscore#五个score
#结果:array([ 0.63919994, 0.71386698, 0.58702344, 0.07923081, -0.25294154])
mean_cvscore=np.mean(cvscore)#平均score
#结果:0.3532759243958823二、Ridge?Regression
from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV#加入parameters多个备选参数由算法决定最佳调参
ridge=Ridge()
parameters={'alpha':[1e-5,1e-10,1e-8,1e-3,1e-2,1,5,10,20,30,35,40,45,50,55,100,200,500,1000]}
ridgeregressor=GridSearchCV(ridge,parameters,cv=5)#parameters喂给ridge,跑五次,cv表示分成五份,一份测试集,四份训练集(五次评分)
ridgeregressor.fit(X,y)
print(ridgeregressor.best_params_)#最佳参数
#结果:{'alpha': 200}
print(ridgeregressor.best_score_)#最佳模型值
#结果:0.49798762179623085
#因为在大范围内选择的最佳参数为200,可以在200左右再选参数,进一步精细化
parameters={'alpha':[170,180,190,200,210,220,230,235,240]}#算法决定最佳调参后可以再进一步精细化
ridgeregressor=GridSearchCV(ridge,parameters,cv=5)#parameters喂给ridge,跑五次
ridgeregressor.fit(X,y)
print(ridgeregressor.best_params_)
#结果:{'alpha': 180}
print(ridgeregressor.best_score_)
#结果:0.49823676810726536cv=5: 平均分成五份,做五次???????
三、Lasso Regression
from sklearn.linear_model import Lasso
from sklearn.model_selection import GridSearchCV
lasso=Lasso()
parameters={'alpha':[1e-5,1e-10,1e-8,1e-3,1e-2,1,5,10,20,30,35,40,45,50,55,100,200,500,1000]}
lassoregressor=GridSearchCV(lasso,parameters,cv=5)#cv表示分成五份,一份测试集,四份训练集(五次评分)
lassoregressor.fit(X,y)
print(lassoregressor.best_params_)
#结果:{'alpha': 1}
print(lassoregressor.best_score_)
#结果:0.431848787926522}四、Ridge?Regression和Lasso Regression
用手动设置训练集和测试集的方式
from sklearn.model_selection import train_test_split#将数据分成测试和训练集
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=0)#测试集占百分之二十,random_state=0随机抽取数据集里的成为测试集
prediction_lasso=lassoregressor.predict(X_test)
prediction_ridge=ridgeregressor.predict(X_test)
prediction_lasso
'''结果:
array([23.74549008, 25.05669894, 27.30699681, 15.26474466, 20.28388223,
22.75172373, 21.45598059, 24.23856649, 21.11819135, 19.95909495,
8.98313974, 13.30218316, 17.99925624, 8.39272295, 35.35448484,
30.78862119, 22.38396018, 34.3159854 , 29.8521009 , 24.63915134,
25.7851669 , 25.20997813, 20.07312698, 29.34704456, 23.54801802,
17.49320154, 19.76581421, 22.02254005, 31.35043449, 19.53061141,
17.86731915, 20.03959005, 22.70589322, 24.27507125, 28.3321545 ,
20.26286175, 10.68729818, 24.94704305, 15.84336797, 12.8254677 ,
25.41186454, 20.63647768, 22.05355817, 16.77749717, 23.30629191,
25.77681736, 19.84379805, 23.32853181, 12.22570134, 23.7054699 ,
21.09270778, 16.76593695, 24.7895207 , 27.77843148, 15.02615536,
21.29343807, 21.55732101, 17.59916216, 18.35971801, 19.53427781,
21.69584327, 22.09466825, 30.77701755, 30.58126341, 18.59617266,
31.00696923, 18.55257582, 18.71479862, 15.79040727, 22.86722623,
21.5804364 , 23.05453916, 30.92223126, 29.21101697, 25.40070956,
5.75970797, 32.88156033, 23.539222 , 26.54430218, 20.38280007,
28.11924474, 19.21283372, 21.96930246, 33.47811935, 33.60083428,
25.39263122, 23.9380826 , 15.60389015, 30.00273357, 17.19181248,
16.84840301, 12.0032218 , 27.14671556, 30.55661543, 25.00026849,
22.52772776, 1.12415573, 28.040647 , 15.35965294, 21.08232769,
24.57837072, 21.89156861])
'''
prediction_ridge
'''结果:
array([23.8221835 , 25.20259785, 27.53093947, 14.58951793, 19.6074286 ,
21.69483525, 21.4566671 , 23.61199647, 20.7368666 , 19.58217475,
6.63735854, 13.94947909, 18.49317999, 7.72499122, 36.3522899 ,
31.18961686, 22.33460779, 34.97976822, 30.83078488, 24.46734842,
25.47472001, 24.6587079 , 20.17171431, 30.01063275, 22.97537586,
15.45690209, 18.90690169, 21.75900952, 32.56455397, 19.74393167,
18.12048305, 20.06946532, 20.97263715, 23.81262096, 28.96841294,
20.7965572 , 10.95091512, 25.35142051, 16.23333426, 13.4982668 ,
24.98278871, 20.39690622, 21.61521524, 16.39149259, 22.65891092,
25.1457976 , 18.73402526, 23.8338197 , 12.33037924, 23.8180197 ,
21.52664928, 17.3346035 , 24.96628962, 27.89463941, 13.76088933,
21.3597084 , 20.75545937, 15.80907985, 16.20859966, 19.5075779 ,
19.53138931, 21.89707787, 31.58387677, 31.47599653, 18.42654404,
31.76658571, 19.22691897, 18.3864344 , 16.63161167, 22.86516713,
21.02865109, 22.53088304, 30.94096598, 29.29650859, 25.49106868,
5.78908343, 34.4337712 , 23.33656159, 26.96978297, 20.25620449,
28.11741719, 18.67996191, 21.59515998, 35.26835166, 35.72684936,
24.86758266, 24.10298707, 15.63298048, 29.91089724, 17.73858371,
15.66579636, 12.72751693, 25.67752193, 30.42846915, 24.23451387,
21.21831042, 0.98960907, 26.86571219, 15.86202673, 19.76164988,
24.74384217, 21.88867704])
'''import seaborn as sns
sns.distplot(prediction_lasso)
sns.histplot(prediction_ridge)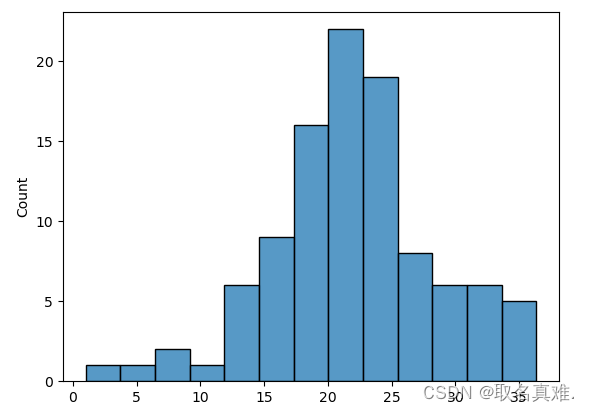
五、对比三种回归的结果
linregrassor.mean_score
#结果:0.3532759243958823
ridgeregressor.best_score_
#结果:0.49798762179623085
lassoregressor.best_score_
#结果:0.431848787926522
对比可知:Ridge?Regression和Lasso Regression在此数据上做线性回归优于Linear Regression本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
