大数据HCIE成神之路之特征工程——特征选择
1.1 特征选择 - Filter方法
1.1.1 实验任务
思考1:特征选择的定义是什么?
- 特征选择(feature selection)也被称为变量选择、属性选择或属性子集选择。它是为了构建模型而选择相关特征子集的过程。
- 特征选择是指从原始特征中挑选出一组最有代表性、分类性能好的特征。
- 没有确定的步骤,更多是工程上的经验和权衡,一般需要耗费较多的时间和精力,掌握常用的经验和权衡方法,可以极大提高挖掘建模的效率和效果。
- 给定不同的挖掘任务,需要的特征组合可能不同。
思考2:为什么要进行特征选择?
现实中大数据挖掘任务,往往特征属性过多,而一个普遍存在的事实是,大数据集带来的关键信息只聚集在部分或少数特征上,因此需要:
- 从中选择出重要的特征使得后续的建模过程只在一部分的特征上构建,减少维数灾难出现的可能。
- 去除不相关的特征,留下关键因素,降低学习任务难度,更容易挖掘数据本身带有的规律;同时在特征选择的过程中,会对数据特征的理解更加充分。
1.1.1.1 实验背景
Filter方法,即过滤法,指的是按照 发散性 或者 相关性 对各个特征进行评分,设定阈值或者待选择阈值的个数,选择特征。是一种启发式方法,它的基本思想是:制定一个准则,用来衡量 每个特征对目标属性的重要性程度 ,以此来对所有特征/属性进行排序,或者进行优选操作,特征选择的过程和后续的学习器无关(区别另外两个方法)。常用的具体技术有下述四种: 方差选择法 、 相关系数法 、 卡方检验 、 互信息法 ,本小节主要围绕这四个方法的实践展开。
思考:什么叫发散性?
回答:在特征选择中,发散性(divergence)是一种衡量特征与目标变量之间差异的度量。它可以用来评估特征与目标变量之间的相关性或相关程度。发散性越大,表示特征与目标变量之间的差异越大,特征对于区分不同类别的样本具有更好的能力。发散性的计算方式可以采用不同的方法,常见的包括信息增益、基尼指数和卡方检验等。
参考学习文章:https://blog.csdn.net/weixin_43378396/article/details/90582108
1.1.1.2 实验目标
利用开源的鸢尾花数据集分别完成Filter方法中的方差选择法、卡方检验方法、相关系数法、互信息法4个具体方法的练习。
1.1.1.3 实验数据解析
鸢尾花数据集来自开源网络,是数据挖掘练习中最常使用的学习数据集,分别有4个特征表征花的不同特点,目标变量target是3种不同的鸢尾花类型。4个特征分别是:sepal length (cm)(花萼长度)、sepal width (cm)(花萼宽度)、petal length (cm)(花瓣长度)、petal width(cm)(花瓣宽度)。目标变量target是三种鸢尾花:setosa(山鸢尾)、versicolor(杂色鸢尾)、virginica(维吉尼亚鸢尾)。
1.1.1.4 实验思路
通过python导入开源鸢尾花数据集,对数据进行简单解读和整合后,通过调用sklearn中的子模块中feature_selection的不同方法或函数分别对鸢尾花数据的特征进行 方差选择法 (调用VarianceThreshold方法),卡方检验法(调用 SelectKBest 函数),互信息法(调用 mutual_info_classif 函数),而相关系数法需单独调用scipy模块中的 stats.pearsonr() 函数直接计算。
1.1.2 实验操作步骤
步骤 1 导入相关模块和鸢尾花数据集模块
Python中sklearn模块的子模块datasets会直接提供该数据集。
import pandas as pd
from pandas import DataFrame as df
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
步骤 2 查看鸢尾花数据集
导入鸢尾花数据包,将 iris.data 部分定义为变量X,将 iris.target 定义为y,即目标变量。此代码中用到concat函数,该函数是在pandas包下的方法,可以将数据根据不同的轴作简单的融合,完整描述如下:
pd.concat( objs, axis=0, join='outer' ) ,主要参数说明objs: series,dataframe或者是panel构成的序列lsit,axis: 需要合并链接的轴, 0是行,1是列 ,join:连接的方式 inner(取交集),或者outer(取并集)。
此处利用该函数将 输入特征 和 目标变量 定义为数据框形式(dataframe)后整合在一起,便于更直观地理解原始数据。代码如下:
iris = load_iris()
X, y = iris.data, iris.target
#以数据框形式查看数据,先定义一个数据框类型的变量
Iris_df=pd.concat([df(X,columns=iris.feature_names),df(y,columns=['target'])],axis=1)
# 随机按列查看数据框的 5 行
Iris_df.sample(5,axis=0)
将数据集写成DataFrame数据框形式输出结果如下:
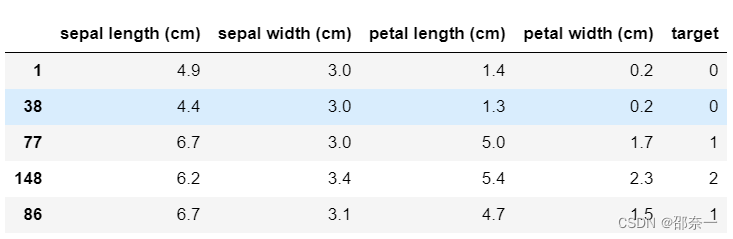
上图可以看出,输入特征X有4个,均是 数值型特征 ,目标变量( target )有三类,分别用0、1、2表示。
步骤 3 利用 方差选择法 对数据集4个特征进行选择
设定阈值threshold为0.5,利用sklearn现有方法对原始4个特征的方差计算,然后筛选方差大于阈值的特征进行保留,代码如下:
from sklearn.feature_selection import VarianceThreshold
X_var=VarianceThreshold(threshold=0.5).fit_transform(X, y) #使用阈值0.5 进行选择
X_var[0:5]#输出方差选择后特征的前 5 行
此处选择sklearn中的子模块中feature_selection的类 VarianceThreshold(threshold=0.0) 实现方差选择法,该方法可以移除数据集中低方差的特征,只有一个参数threshold:float,选填,默认为0,表示指定删除训练集特征的方差的阈值,此处指定的阈值为0.5,即特征方差小于0.5的特征会被删除;VarianceThreshold( )还有一个属性variances_:可以输出样本集中每个特征的具体方差值。
输出结果如下:
array([[5.1, 1.4, 0.2],
? [4.9, 1.4, 0.2],
? [4.7, 1.3, 0.2],
? [4.6, 1.5, 0.2],
? [5. , 1.4, 0.2]])
此时继续执行
Iris_df.head(5)
输出结果如下:
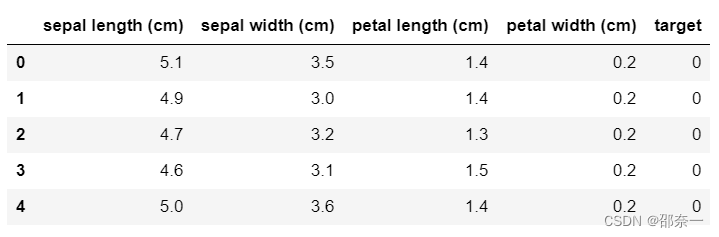
通过上述输出结果对比可以发现,方差大于0.5的特征只有第 1、3、4 个特征,所以被保留下来,即利用方差选择法保留下的特征。
思考3:阈值一般取多少?
回答:阈值的选择取决于数据集和问题。方差选择法可以用于剔除低方差特征。阈值的设定需要综合考虑特征的方差分布、任务需求和模型性能。较高的阈值会保留方差较大的特征,而较低的阈值可能保留方差较小的特征。通过观察特征方差的分布情况,可以初步选择一个阈值,并进行实验和交叉验证来调整阈值,以找到最佳的性能和特征选择结果。需要注意的是,过高或过低的阈值可能导致信息损失或维度过高的问题。因此,阈值的选择是一个经验性的过程,需要根据具体情况进行调整和优化。
步骤 4 利用 相关系数法 对数据集4个特征进行选择
Scipy的 pearsonr方法 能够同时计算相关系数r值和p-value(简称p值), p值越小,表示相关系数越显著。利用for循环分别对X中的每个特征与目标y计算相关系数值,代码如下:
from scipy import stats
for i in range(X.shape[1]):
X_pear = stats.pearsonr(X[:,i], y)
print(X_pear)
输出结果如下:
PearsonRResult(statistic=0.7825612318100814, pvalue=2.8904783526140384e-32)
PearsonRResult(statistic=-0.4266575607811244, pvalue=5.2015632551773126e-08)
PearsonRResult(statistic=0.9490346990083885, pvalue=4.2018731529627324e-76)
PearsonRResult(statistic=0.9565473328764029, pvalue=4.1553110153181703e-81)
解释:
X_pear 是一个 PearsonRResult 对象,其中包含了皮尔逊相关系数和 p 值的信息。
statistic=0.9565473328764029:这是特征与目标变量之间的皮尔逊相关系数。皮尔逊相关系数的取值范围为 -1 到 1,其中 1 表示完全正相关,-1 表示完全负相关,0 表示没有线性相关性。在这种情况下,相关系数为 0.9565473328764029,表示特征与目标变量之间具有很强的正相关关系。
pvalue=4.1553110153181703e-81:这是皮尔逊相关系数的 p 值。p 值是用来评估相关系数的显著性的指标。它表示在原假设为特征与目标变量之间不存在线性相关关系的情况下,观察到的相关系数或更极端的情况发生的概率。在这种情况下,p 值非常接近于 0,远小于通常使用的显著性水平(例如 0.05),表明相关系数是显著的,即特征与目标变量之间很可能存在着显著的线性相关关系。
如上分别输出了X中4个特征与y计算的相关系数r值和p值,可以看到第4个特征与目标y的相关值最大,即相关性最大,其p值为4.1554775794971695e-76,远小于0.05,表明该相关性关系是显著的。
步骤 5 利用 卡方检验法 选择最好的两个特征
SelectKBest 移除得分前 k 名以外的所有特征(取top k),方法具体为:
sklearn.feature_selection.SelectKBest(score_func=<function f_classif>, k=10),
主要参数如下:
- score_func:可调用的评分函数,也就是此处选择的特征选择方法,如此处选择
卡方检验方法,其函数名称为chi2,并返回一对数组(得分,pvalues)或带有分数的单个数组。默认值为f_classif(适用于分类任务)。 - k:int或“all”,可选,默认= 10,表示所选特征数。
主要属性为: - scores_:array-like,shape =(n_features,),即该特征在该特征选择方法下的得分;
- pvalues_:array-like,shape =(n_features,),特征分数的p值,如果score_func仅返回分数,则为无。
此处设定score_func= chi2,即调用函数为卡方检验,设定保留特征数k=2,代码如下:
X_chi2 = SelectKBest(chi2, k=2).fit_transform(X, y)
X_chi2[0:4]
输出结果如下:
array([[1.4, 0.2],
? [1.4, 0.2],
? [1.3, 0.2],
? [1.5, 0.2]])
与前面查看到的特征数据相比可发现,卡方检验保留的是第3个和第4个特征。
步骤 6 利用 互信息法 查看各个特征与目标变量相关性
互信息方法不需要事先指定参数,只需要选择方法 mutual_info_classif ,输入特征集和目标变量,就会计算出特征集X每个特征与目标y之间的互信息值大小,代码如下:
from sklearn.feature_selection import mutual_info_classif
X_mut = mutual_info_classif(X, y)
X_mut
输出结果如下:
array([0.5054192 , 0.26410863, 0.98610491, 0.98037258])
选择互信息值大的特征作为保留特征,可以从结果看出互信息最大的特征依次是第3个、第4个、第1个与第2个,可以再依据需要保留特征。
1.2 特征选择 - Wrapper方法
1.2.1 实验任务
1.2.1.1 实验背景
Wrapper,包装法,也形象地称为“弯刀法”,它解决思路没有过滤法直接,它是在确认后续的算法模型后,把模型本身的性能作为评价准则:选择一个目标函数来一步步的筛选特征。常用包装法是递归特征消除法,简称RFE,使用一个基模型来进行多轮训练,每轮训练后,移除若干权值系数的特征,再基于新的特征集进行下一轮训练。
1.2.1.2 实验目标
利用鸢尾花数据集完成Wrapper方法中递归特征消除法的练习,掌握RFE方法的思想和使用。
1.2.1.3 实验数据解析
鸢尾花数据集来自开源网络,是数据挖掘练习中最常使用的学习数据集,分别有4个特征表征花的不同特点,目标变量target是3种不同的鸢尾花类型。4个特征分别是:sepal length (cm)(花萼长度)、sepal width (cm)(花萼宽度)、petal length (cm)(花瓣长度)、petal width(cm)(花瓣宽度)。目标变量target是三种鸢尾花:setosa(山鸢尾)、versicolor(杂色鸢尾)、virginica(维吉尼亚鸢尾)。
1.2.1.4 实验思路
通过python导入开源鸢尾花数据集,对数据进行简单解读和整合后,调用sklearn中的子模块中feature_selection的 RFE方法 和sklearn中的子模块linear_model中的逻辑回归方法 LogisticRegressio() 作为后续调用的基模型,对鸢尾花数据的特征进行筛选,最后还打印出模型详情和关键参数,帮助读者充分掌握RFE方法的思想和使用。
1.2.2 实验操作步骤
步骤 1 导入RFE方法需要的相关模块和鸢尾花数据集,并查看数据前5行
调用sklearn中的子模块中feature_selection的RFE方法和sklearn中的子模块linear_model中的逻辑回归方法LogisticRegressio()作为后续调用的基模型,并对数据进行简单解读和整合。
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
# 利用开源数据 - 鸢尾花数据集进行特征选择
from sklearn.datasets import load_iris
iris = load_iris()
X, y = iris.data, iris.target
print(X.shape)
print(X[0:5])
输出结果如下:
(150, 4)
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
步骤 2 调用RFE方法,对鸢尾花数据集进行训练
训练后的模型,可以打印出模型和参数进行观察。
#RFE 方法的参数 estimator 表示选择的基模型,此处选用逻辑回归算法,特征保留 3 个。
x_rfe=RFE(estimator=LogisticRegression(), n_features_to_select=3).fit(X, y)
x_rfe
输出结果如下:
RFE(estimator=LogisticRegression(max_iter=1000), n_features_to_select=3)
结果可以看到调用模型的完整描述。
步骤 3 查看RFE方法的一些关键属性
print(x_rfe.n_features_ ) # 所选特征的数量
print(x_rfe.support_ ) # 按特征对应位置展示所选特征,True 表示保留,False 表示剔除。
print(x_rfe.ranking_ ) # 特征排名,使得 ranking_[i]对应于第 i 个特征的排名位置,1 表示最优特征。
print(x_rfe.estimator_ ) # 递归方法选择的基模型
输出结果如下:
3
[False True True True]
[2 1 1 1]
LogisticRegression(max_iter=1000)
可以看到,该方法输出需要保留的3个特征分别是第2、3、4这三个,用的基础算法是 逻辑回归算法 ,在学习了其他有监督学习后,此处读者可以尝试调用其他有监督算法查看不同效果。
步骤 4 查看RFE方法训练后特征选择的结果
print(x_rfe.transform(X)[0:5])#显示前 5 行
输出结果如下:
[[3.5 1.4 0.2]
[3. 1.4 0.2]
[3.2 1.3 0.2]
[3.1 1.5 0.2]
[3.6 1.4 0.2]]
对比原始数据可以看出此结果保留的是第2、3、4三个特征。
1.3 特征选择 - Embedding方法
1.3.1 实验任务
1.3.1.1 实验背景
Embedded,即嵌入法,相比前两种方法更加复杂,它利用机器学习算法和模型进行训练,得到各个特征的 权值系数 ,根据权值系数从大到小来选择特征。常用嵌入法技术主要有两类方法: 线性模型 和 正则化 ,其中包括具体的练习有2个:基于线性回归模型方法、基于L1的正则化方法;另一类是基于树模型的特征选择,这里仅练习基于随机森林的嵌入方法,随机森林具有准确率高、稳定性强、易于使用等优点,是目前最流行的机器学习算法之一,基于随机森林的预测模型能够用来计算特征的重要程度,因此能用来去除不相关的特征。
1.3.1.2 实验目标
本小结的练习具体分3个任务,具体目标如下:
-
基于线性回归模型方法:该方法比较简单,强调理解,帮助读者理解后续的其他方法和直观的掌握嵌入法思想;
-
基于L1的正则化方法,该方法比较重要常用,也有一定难度,读者可以先在本节掌握其使用方法,在学习本系列课程的第5章无监督学习和第8章模型评估后,进一步掌握其思想和优缺点;
-
基于随机森林的嵌入方法,该方法重要且常用,读者可以先在本节掌握其使用方法,在学习本系列课程的第5章无监督学习后,进一步掌握其思想和优缺点。
1.3.1.3 实验数据解析
本小结的练习具体分3个任务,使用的数据解析如下:
-
基于线性回归模型方法:该部分的实验数据可以通过python中numpy库下的随机数生成模块random直接生成。利用随机函数
numpy.random.seed(num),随机生成一组服从正态分布且有3个特征的数据集进行建模; -
基于L1的正则化方法和基于随机森林的嵌入方法均使用开源的波士顿房价数据集,通过调用
sklearn.datasets.load_boston可加载相关数据。该数据集共有 506 个记录,13 个原始输入特征和1个目标变量。
13个特征的解释如下:
- CRIM:城镇人均犯罪率。
- ZN:住宅用地超过 25000 sq.ft的比例。
- INDUS:城镇非零售商用土地的比例。
- CHAS:查理斯河空变量(如果边界是河流,则为1;否则为0)。
- NOX:一氧化氮浓度。
- RM:住宅平均房间数。
- AGE:1940年之前建成的自用房屋比例。
- DIS:到波士顿五个中心区域的加权距离。
- RAD:辐射性公路的接近指数。
- TAX:每 10000 美元的全值财产税率。
- PTRATIO:城镇师生比例。
- B:1000(Bk-0.63)^ 2,其中 Bk 指代城镇中黑人的比例。
- LSTAT:人口中地位低下者的比例。
- MEDV:自住房的平均房价,以千美元计。
目标变量target表示房价。
1.3.1.4 实验思路
本小节练习分3个任务,是嵌入法常见的处理技术,各个任务的具体思路是:
-
基于线性回归模型方法:导入回归模型模块和随机数生成模块,生成随机数据,利用线性回归模型对生成的数据拟合,建立一个回归模型,通过打印模型的具体形式,观察线性回归各个自变量的系数,也就是每个特征的权重,数值越大的,对应的特征越应该被保留。
-
基于L1的正则化方法,直接通过sklearn导入开源的波士顿房价数据集和数据处理、建模模块,对房价数据的13个特征和目标变量进行整合,标准化后,直接调用
LASSO( )方法对处理后的数据进行建模,该方法的自带属性coef_会输出建模过程中13个特征的对应系数,系数值越大,该特征对目标的重要性越大,越需要被保留。 -
基于随机森林的嵌入方法,依然使用波士顿房价数据,通过pandas,sklearn导入处理、建模模块,直接调用随机森林回归方法
RandomForestRegressor( )对数据进行建模,该方法的自带属性feature_importances_会输出建模过程中13个特征的重要性评分,评分越高,表明该特征对目标的影响越大,越需要被保留。
1.3.2 实验操作步骤
1.3.2.1 基于线性回归模型方法
对于满足回归关系的数据分布,可以利用回归模型的系数来选择特征,原理是越重要的特征,在模型中对应的系数就会越大,而跟输出变量越是无关的特征,对应的系数就会越接近于0。
步骤 1 导入相关模块
导入linear_model模块内的LinearRegression方法,几个参数介绍如下(也可以通过help(LinearRegression)查看该方法的详细描述):
- fit_intercept:bool型,选择是否需要计算截距,默认为True,如果中心化了的数据可以选择false;normalize:bool型,选择是否需要标准化(中心化),默认为false,和参数fit_intercept有关;
- copy_x:bool型,选择是否复制数据,默认True复制,如果输入False,可能会因为中心化把X数据覆盖;
- n_job:int型,选择几核用于计算,默认1,-1表示全速运行。代码如下:
from sklearn.linear_model import LinearRegression
import numpy as np
步骤 2 随机生成实验数据
该部分的实验数据可以通过python中numpy库下的随机数生成模块random直接生成。
利用随机函数numpy.random.seed(num),随机生成一组服从正态分布且有3个特征的数据集进行建模,其中numpy.random.seed(num):如果使用相同的num,则每次生成的随机数都相同。如果不设置这个值,则系统根据时间来自己选择这个值,此时每次生成的随机数因时间差异而不同。
np.random.seed(0)
size = 5000
# 创建一个有 3 个特征的随机数据集
X = np.random.normal(0, 1, (size, 3))
#设定 Y = X0 + 2*X1 + noise
Y = X[:,0] + 2*X[:,1] + np.random.normal(0, 2, size)
查看生成数据。
print(X[0:5])
print(Y[0:5])
输出结果如下:
[[ 1.76405235 0.40015721 0.97873798]
[ 2.2408932 1.86755799 -0.97727788]
[ 0.95008842 -0.15135721 -0.10321885]
[ 0.4105985 0.14404357 1.45427351]
[ 0.76103773 0.12167502 0.44386323]]
以及,
[ 7.50433081 7.15004266 -0.14733131 1.56578492 2.00498194]
创建线性回归模型对数据进行拟合
lr = LinearRegression()
lr.fit(X, Y)
输出结果如下:
LinearRegression()
步骤 3 打印出建立好的回归模型公式
通过定义打印函数,可以打印出已经建立的回归模型函数,直观地观察每个特征的系数大小,然后保留系数大的值对应的特征。
def pretty_print_linear(coefs, names = None, sort = False):
if names == None:
names = ["X%s" % x for x in range(len(coefs))]
lst = zip(coefs, names)
if sort:
lst = sorted(lst, key = lambda x:-np.abs(x[0]))
return " + ".join("%s * %s" % (round(coef, 3), name) for coef, name in lst)
print("Linear model:", pretty_print_linear(lr.coef_))
输出结果如下:
Linear model: 0.984 * X0 + 1.995 * X1 + -0.041 * X2
可以看到,第2个特征X1的系数为1.995,是相对另外两个特征来说,对目标特征最重要的特征,最应该被保留下来。
1.3.2.2 基于L1的正则化方法
本小节旨在利用L1的正则化特征选择方法对波士顿房价数据集的13个特征进行选择。实验具体步骤如下:
步骤 1 导入相关模块
导入波士顿数据集所在模块,L1正则化所用到的方法LASSO,以及对数据集进行标准化处理的模块StandardScaler和数据框整合模块pandas. DataFrame。
from sklearn.datasets import load_boston #sklearn 自带的小型数据集包
from sklearn.linear_model import Lasso
from sklearn.preprocessing import StandardScaler
from pandas import DataFrame as df
import pandas as pd
步骤 2 导入模块自带的数据集
导入模块sklearn.datasets.load_boston自带的数据集,并且查看数据集特征和目标变量,形状和特征名称等特征信息。
boston = load_boston()
scaler = StandardScaler()
X = scaler.fit_transform(boston["data"])
Y = boston["target"]
#以数据框形式查看数据,先定义一个数据框类型的变量。
boston_df=pd.concat([df(X,columns=boston.feature_names),df(Y,columns=['target'])],axis=1)
# 随机按列查看数据框的 5 行
boston_df.sample(5,axis=0)
输出结果如下:

上图可以看出13个特征和目标变量均是数值型的类型。
步骤 3 导入L1正则化模型并训练数据
代码中调用的模型完整描述为:
class sklearn.linear_model.Lasso(alpha=1.0, fit_intercept=True, normalize=False, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection=’cyclic’)
主要参数意义如下:
- alpha:float,可选,即惩罚项前的系数,常数乘以L1项。默认为1.0。 alpha = 0相当于普通的最小二乘,由LinearRegression对象求解。不建议在Lasso对象中使用alpha = 0。
- fit_intercept:boolean,optional,默认为True,是否计算此模型的截距。如果设置为False,则不会在计算中使用截距。
- normalize:布尔值,可选,默认为False,当fit_intercept设置为False时,将忽略此参数。如果为True,则回归量X将在回归之前通过减去平均值并除以L2范数来归一化。如果希望标准化,需要在使用
normalize = False的估算器调用fit之前sklearn.preprocessing.StandardScaler。
关键属性说明如下:
- coef_:每个特征的系数值,也就是每个特征对目标影响的重要性,值越大越重要。
此处调用方法的操作如下,仅指定参数alpha,代码如下:
lasso = Lasso(alpha=1) # alpha 为 float 类型,可选,默认 1.0。当 alpha 为0 时算法等同于普通最小二乘法,不建议将 alpha 设为 0.
#训练数据
lasso.fit(X, Y)
输出模型如下:
Lasso(alpha=1)
可以看到该L1正则化模型正则项系数确实为1。
步骤 4 打印训练后模型各个特征系数
查看各特征变量对应系数,非零系数即为保留特征,系数值越大的特征越重要。
for i in range(X.shape[1]):
print(boston.feature_names[i],format(lasso.coef_[i], '.3f'))
输出结果如下:
CRIM -0.000
ZN 0.000
INDUS -0.000
CHAS 0.000
NOX -0.000
RM 2.713
AGE -0.000
DIS -0.000
RAD -0.000
TAX -0.000
PTRATIO -1.344
B 0.181
LSTAT -3.543
可以看到非零特征有4个,可以保留这4个特征。如果希望增加保留的特征数,可以通过调整参数alpha的值,令alpha小于1的值进行调试。反之,可以看到很多特征的系数都是0。如果继续增加alpha的值,得到的模型就会越来越稀疏,即越来越多的特征系数会变成0。然而,L1正则化像非正则化线性模型一样也是不稳定的,如果特征集合中具有相关联的特征,当数据发生细微变化时也有可能导致很大的模型差异。
1.3.2.3 基于随机森林的嵌入方法
该节实验仍利用开源数据集:波士顿房价数据集。
步骤 1 调用相关模块
#使用 sklearn 的随机森林回归对波士顿房价集特征筛选
from sklearn.datasets import load_boston #sklearn 自带的小型数据集包
from sklearn.ensemble import RandomForestRegressor
from pandas import DataFrame as df
from sklearn.preprocessing import StandardScaler
步骤 2 导入模块自带的数据集并且定义好输入特征和目标特征。
boston = load_boston()
scaler = StandardScaler()
X = scaler.fit_transform(boston["data"])
y = boston["target"]
步骤 3 调用随机森林回归方法进行训练数据。
调用class sklearn.ensemble.RandomForestRegressor方法,随机森林回归方法的完整描述为:
class sklearn.ensemble.RandomForestRegressor ( n_estimators=’warn’, criterion=’mse’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=’auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False )
其中主要参数说明为如下:
-
n_estimators:整数,可选(默认= 10),即森林里的树木数量。在版本0.20中:n_estimators的默认值将从版本0.20中的10更改为版本0.22中的100。
-
criterion:衡量分裂质量的标准。支持的标准是均方误差的“mse”,等于作为特征选择标准的方差减少,以及平均绝对误差的“mae”。
-
max_depth:整数或无,可选(默认=无),树的最大深度。如果为None,则扩展节点直到所有叶子都是纯的或直到所有叶子包含少于min_samples_split样本。
-
min_samples_split:拆分内部节点所需的最小样本数:如果是int,则将min_samples_split视为最小数字。如果为float,则min_samples_split为分数,ceil(min_samples_split * n_samples)为每个分割的最小样本数。
主要的属性说明:
-
estimators_:DecisionTreeRegressor列表,拟合子估算器的集合。
-
feature_importances_:返回每个特征的重要性(数值越高,功能越重要)。
-
n_features_:执行时的特征数,此处为13。
在对波士顿房价数据集进行建模的操作中,先调用随机森林回归方法,指定相关参数,指定森林中树的个数是15,即n_estimators=15;每棵树的最大深度是6,即max_depth=6,再用该方法训练数据,输出波士顿房价数据集X中13个特征的重要性。调用代码如下:
# 调用随机森林回归方法
rf = RandomForestRegressor(n_estimators=15, max_depth=6)
# 调用方法训练数据
boston_rf=rf.fit(X, y)
# 查看模型的属性 feature_importances_,表示建模过程中对每个特征的重要性评分
for i in range(X.shape[1]):
print(boston.feature_names[i],format(boston_rf.feature_importances_[i], '.3f')) #查看各特征重要性
输出结果如下:
CRIM 0.041
ZN 0.001
INDUS 0.002
CHAS 0.001
NOX 0.022
RM 0.435
AGE 0.009
DIS 0.056
RAD 0.003
TAX 0.012
PTRATIO 0.009
B 0.008
LSTAT 0.399
可以看到13个特征依次带着其重要性大小输出,在此模型中,最重要的4个特征依次是: RM 0.435 , LSTAT 0.399 , DIS 0.056 和 CRIM 0.041 。
利用随机森林方法进行特征选择,特征重要性的得分存在不稳定的现象,这不仅仅是随机森林特有的,大多数基于模型的特征选择方法都存在这个问题。可以通过调整参数,多次执行或者交叉验证获取一个较稳定的结果;或者尝试多种方法,将几种方法的结果对比考虑。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!