【数据结构】二叉搜索(查找/排序)树
一、二叉搜索树基本概念
1、定义
二叉搜索树,又称为二叉排序树,二叉查找树,它满足如下四点性质:
1)空树是二叉搜索树;
2)若它的左子树不为空,则左子树上所有结点的值均小于它根结点的值;
3)若它的右子树不为空,则右子树上所有结点的值均大于它根结点的值;
4)它的左右子树均为二叉搜索树;
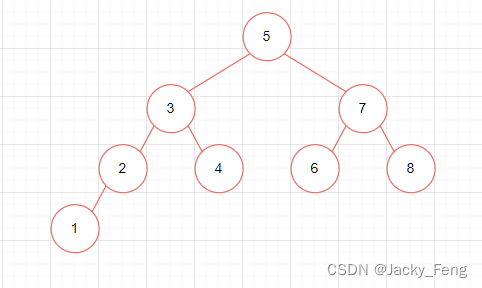
?如上图所示:二叉搜索树的任何一棵子树,它的根结点的值一定大于左子树所有结点的值,且一定小于右子树所有结点的值。如果对二叉搜索树进行中序遍历,我们可以发现,得到的序列是一个递增序列,上述的遍历结果为[1,2,3,4,5,6,7,8]。
如果要查找4,只需要从根结点比较查找3次就能找到,可以显著提高搜索的速度。
二、二叉搜索树基础操作
1、查找算法
(1)查找原理
在二叉搜索树中查找某个数是否存在,存在返回 true,不存在返回 false。
对于要查找的数 val ,从根结点出发,总共四种情况依次判断:
1)若二叉搜索树为空树,直接返回 false;
2) val 的值 等于?树根结点的值,则直接返回 true;
3) val 的值 小于?树根结点的值,说明 val 对应的结点不在根结点,也不在右子树上,需要在左子树上查找,递归返回左子树的查找结果;
4) val 的值 大于?树根结点的值,说明 val 对应的结点不在根结点,也不在左子树上,需要在右子树上查找,递归返回右子树的查找结果;
(2)查找算法源码
① 结点源码
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};② 查找算法源码 (深度优先,递归查找)
bool BSTFind(TreeNode* root, int val)
{
if (root == nullptr) {
return false;
}
if (root->val == val) {
return true;
}
if (val < root->val) {
return BSTFind(root->left, val);
}
else {
return BSTFind(root->right, val);
}
}2、插入算法
(1)插入原理
将给定的值 val 生成结点后,插入到树上的某个位置,并且保持这棵树还是二叉搜索树。对于要插入的值 val ,从根结点出发,总共四种情况依次判断:
1)若为空树,则创建一个值为 val 的结点并且返回根结点;
2) val 的值 等于?树根结点的值,无须执行插入,直接返回根结点;
3) val 的值 小于?树根结点的值,那么插入位置一定在?左子树,递归执行插入左子树的过程,并且返回插入结果作为新的左子树;
4) val 的值 大于?树根结点的值,那么插入位置一定在?右子树,递归执行插入右子树的过程,并且返回插入结果作为新的右子树;
(2) 插入源码
TreeNode* BSTInsert(TreeNode* root, int val) {
if (root == nullptr) {
root = new TreeNode(val);
return root;
}
if (val == root->val) {
return root;
}
if (val < root->val) {
root->left = BSTInsert(root->left, val);
}
else {
root->right = BSTInsert(root->right, val);
}
return root;
}3、删除算法
(1)删除原理
删除值为 val 结点,从根结点出发,总共四种情况依次判断:
1)空树,不存在结点直接返回空树;
2) val 的值 小于?树根结点的值,则需要删除的结点一定不在右子树上,递归调用删除左子树的对应结点;
3) val 的值 大于?树根结点的值,则需要删除的结点一定不在左子树上,递归调用删除右子树的对应结点;
4) val 的值 等于?树根结点的值,相当于是要删除根结点,这时候又要分三种情况:
- 当前树只有左子树,则直接将左子树返回,并且释放当前树根结点的空间;
- 当前树只有右子树,则直接将右子树返回,并且释放当前树根结点的空间;
- 当左右子树都存在时,需要在右子树上找到一个值最小的结点,替换新的树根,而其它结点组成的树作为它的子树;
(2)删除源码
由上述删除算法原理可知,删除结点之前可能还需要找最小结点,所以需要定义查找最小结点接口。
int BSTFindMin(TreeNode* root) {
if (root->left)
return BSTFindMin(root->left);
return root->val;
}查找根为 root ,值最小的那个结点的值,根据二叉搜索树的性质,如果左子树存在,则必然存在更小的值,递归搜索左子树,且最小值结点为叶子结点;如果左子树不存在,则根结点的值必然最小,直接返回。
删除根结点,并返回新根结点
//删除根结点并返回新根结点
TreeNode* Delete(TreeNode* root) {
TreeNode* delNode, * retNode;
if (root->left == nullptr) {
delNode = root;
retNode = root->right;
delete delNode;
delNode = nullptr;
}
else if (root->right == nullptr) {
delNode = root;
retNode = root->left;
delete delNode;
delNode = nullptr;
}
else {
retNode = BSTFindMin(root->right);
retNode->left = root->left;
retNode->right = root->right;
delete root;
root = nullptr;
}
return retNode;
}- 如果左子树为空,则用右子树做为新的树根;
- 如果右子树为空,则用左子树作为新的树根;
- 否则,当左右子树都为非空时,利用?BSTFindMin?,从右子树上找出最小的结点,作为新的根。
删除指定值的结点
//删除指定结点
TreeNode* BSTDelete(TreeNode* root, int val) {
if (nullptr == root) {
return nullptr;
}
if (val == root->val) {
return Delete(root);
}
else if (val < root->val) {
root->left = BSTDelete(root->left, val);
}
else if (val > root->val) {
root->right = BSTDelete(root->right, val);
}
return root;
}- 如果为空树,则直接返回空结点;
- 如果需要删除的结点的值 等于?树根结点的值,则直接调用接口?Delete?;
- 如果需要删除的结点的值 小于?树根结点的值,则需要删除的结点必定在左子树上,递归调用左子树的删除,并且将返回值作为新的左子树的根结点;
- ?如果需要删除的结点的值 大于?树根结点的值,则需要删除的结点必定在右子树上,递归调用右子树的删除,并且将返回值作为新的右子树的根结点;
- 返回当前树的根结点;
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!