数据结构学习 jz10斐波那契数列

题目：

---

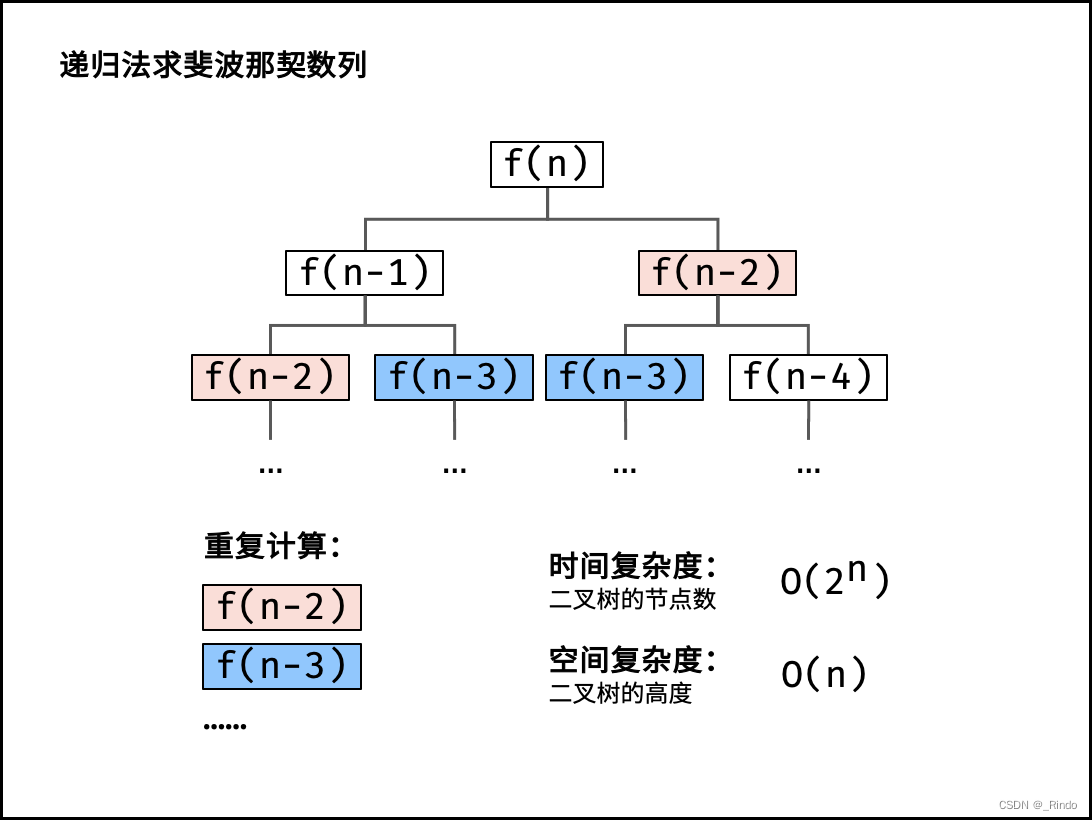
解法一：暴力递归

太慢了 要递归两次 而且很多重复计算

原理： 把 f(n)问题的计算拆分成 f(n?1)和f(n?2) 两个子问题的计算，并递归，以f(0) 和 f(1)为终止条件。
缺点： 大量重复的递归计算，例如f(n) 和f(n?1) 两者向下递归需要 各自计算f(n?2) 的值

时间复杂度O(N^2)
空间复杂度O(N) 前后各开了一个栈给递归

#include <iostream>
//解法一：暴力递归 太慢了 要递归两次
//时间复杂度O(N^2)
//空间复杂度O(N)前后各开了一个栈给递归
class Solution {
public:
    int fib(int n) {

        return add_fib(n);
    }
    int add_fib(int n)
    {
        if (n == 0)return 0;
        if (n == 1)return 1;
        int a = add_fib(n - 1) + add_fib(n - 2);
        return a;
    }
};

void Test_solution1()
{
    Solution solution;
    std::cout<<solution.fib(4);
}

---

解法二：?记忆化递归 哈希

因为暴力递归会有很多重复的计算，所以想要用一个哈希表把已经计算过的结果存起来。这样就可以减少时间啦！

原理： 在递归法的基础上，新建一个长度为 n?的数组，用于在递归时存储 f(0) 至 f(n) 的数字值，重复遇到某数字则直接从数组取用，避免了重复的递归计算。
缺点： 记忆化存储需要使用 O(N) 的额外空间。

时间复杂度O(N)
空间复杂度O(N) 多弄了个哈希

其实也可以用别的容器，我单纯觉得我应该要多用用哈希表，所以才用的哈希表（用哈希表感觉莫名其妙很帅！

#include <iostream>
#include <unordered_map>
//解法二：记忆化递归 哈希
//时间复杂度O(N)
//空间复杂度O(N)
class Solution {
public:
    int fib(int n) {
        hmap[0] = 0;
        hmap[1] = 1;
        return add_fib(n);
    }
    int add_fib(int n)
    {
        if (n == 0)return 0;
        if (hmap[n] != 0)
            return hmap[n];
        hmap[n] = (add_fib(n - 1) + add_fib(n - 2)) % 1000000007;
        return hmap[n];
    }
private:
    std::unordered_map<int, int> hmap;
};

void Test_solution2()
{
    Solution solution;
    std::cout << solution.fib(100);
}

---

解法三：动态规划

我觉得这个的动态规划写的挺好的：https://leetcode.cn/problems/fei-bo-na-qi-shu-lie-lcof/solutions/101593/mian-shi-ti-10-i-fei-bo-na-qi-shu-lie-dong-tai-gui/

时间复杂度：O(n)
空间复杂度：O(1)

递归版：（我写的）

#include <iostream>
#include <vector>
//解法三：动态规划 第一个是递归版 第二个是for循环版
// 时间复杂度：O(n)
//空间复杂度：O(1)
class Solution {
public:
    int fib(int n) {
        if (n <= 1)return n;
        add_fib(n);
        return b;
    }
    void add_fib(int n)
    {
        if (n <= 1)return;
        add_fib(n - 1);
        sum = (a + b) % 1000000007;
        a = b;
        b = sum;
    }
private:
    int a = 0, b = 1, sum;
};

for循环版： （看了别人的之后写的，仿写）

class Solution {
public:
    int fib(int n) {
        if (n <= 1)return n;
        for (int i = 1; i < n; ++i)
        {
            sum = (a + b) % 1000000007;
            a = b;
            b = sum;
        }
        return b;
    }
private:
    int a = 0, b = 1, sum;
};

---

解法四：矩阵快速幂

这是一种非常巧妙的方法，应该也是这种题目的最优解了！我觉得很有趣，可以大大节省时间，非常好的！

具体实现原理可以去看我的笔记或者这一篇文章

关键就是要找到斐波那契的递推式，然后有了递推式就可以使用快速幂了！

时间复杂度O(logn)
空间复杂度O(1)

代码部分：

前面struct matrix是创建矩阵对象。

后面的matrix qpow_fib(matrix a, int n)是用矩阵快速幂求斐波那契数列的矩阵的幂。

#include <iostream>
#include <vector>
#define MOD 1000000007
//解法四：矩阵快速幂
//由快速幂推导而来
// 时间复杂度O(logn)
// 空间复杂度O(1)
//注意1：斐波那契数列的矩阵公式推导，递推式是很难找的！
//注意2：单位矩阵和斐波那契的矩阵
struct matrix//矩阵对象
{
	long long a1, a2, b1, b2;
	matrix(long long a1, long long a2, long long b1, long long b2) :a1(a1), a2(a2), b1(b1), b2(b2) {}
	matrix operator*(const matrix& y)//两个矩阵相乘
	{
		matrix ans(
			(a1 * y.a1 + a2 * y.b1) % MOD,
			(a1 * y.a2 + a2 * y.b2) % MOD,
			(b1 * y.a1 + b2 * y.b1) % MOD,
			(b1 * y.a2 + b2 * y.b2) % MOD
		);
		return ans;
	}
};
class Solution {
public:
    long long fib(int n) {
		if (n == 0)return 0;
		matrix M(0, 1, 1, 1);//注意这里是斐波那契数列推导的矩阵
		matrix ans = qpow_fib(M, n - 1);//这里求的是M^(n-1)：底数是M，幂是n-1
		long long result = (ans.a1 + ans.a2) % MOD;//求的是F(n)
		return result;
    }
private:
	matrix qpow_fib(matrix a, int n)
	{
		matrix ans(1, 0, 0, 1);//是单位矩阵
		//|1  0|
		//|0  1|
		while (n)
		{
			if (n & 1)
				ans = a * ans;
			a = a * a;
			n >>= 1;
		}
		return ans;
	}
};
void Test_solution4()
{
    Solution solution;
    std::cout << solution.fib(100);
}

---

测试结果：

我发现这个时间非常玄学？