Python 全栈体系【四阶】(六)
第四章 机器学习
五、线性模型
1. 概述
线性模型是自然界最简单的模型之一,它描述了一个(或多个)自变量对另一个因变量的影响是呈简单的比例、线性关系。例如:
住房每平米单价为 1 万元,100 平米住房价格为 100 万元,120 平米住房为 120 万元;
一台挖掘机每小时挖 100 m 3 100m^3 100m3沙土,工作 4 小时可以挖掘 400 m 3 400m^3 400m3沙土.。
线性模型在二维空间内表现为一条直线,在三维空间内表现为一个平面,更高维度下的线性模型很难用几何图形来表示(称为超平面)。如下图所示:

二维空间下线性模型表现为一条直线
二维空间下线性模型表现为一条直线
二维空间下线性模型表现为一条直线
?
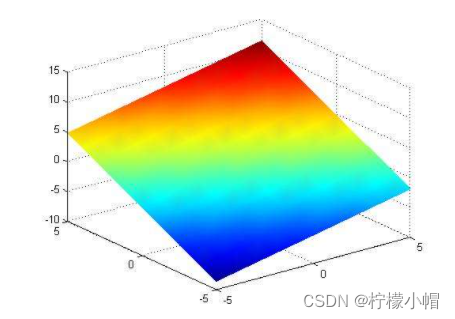
三维空间下线性模型表现为一个平面
三维空间下线性模型表现为一个平面
三维空间下线性模型表现为一个平面
?
线性回归是要根据一组输入值和输出值(称为样本),寻找一个线性模型,能最佳程度上拟合于给定的数值分布,从而再给定新的输入时预测输出.样本如下表所示:
| 输入(x) | 输出(y) |
|---|---|
| 0.5 | 5.0 |
| 0.6 | 5.5 |
| 0.8 | 6.0 |
| 1.1 | 6.8 |
| 1.4 | 6.8 |
根据样本拟合的线性模型如下图所示:
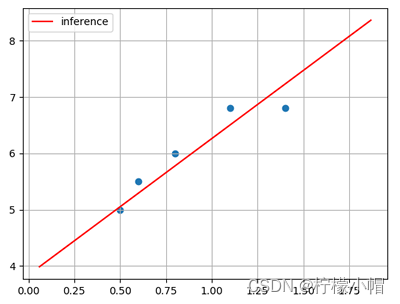
2. 线性模型定义
设给定一组属性 x , x = ( x 1 ; x 2 ; . . . ; x n ) x, x=(x_1;x_2;...;x_n) x,x=(x1?;x2?;...;xn?),线性方程的一般表达形式为:
y = w 1 x 1 + w 2 x 2 + w 3 x 3 + . . . + w n x n + b y = w_1x_1 + w_2x_2 + w_3x_3 + ... + w_nx_n + b y=w1?x1?+w2?x2?+w3?x3?+...+wn?xn?+b
写成向量形式为:
y = w T x + b y = w^Tx + b y=wTx+b
其中,
w
=
(
w
1
;
w
2
;
.
.
.
;
w
n
)
,
x
=
(
x
1
;
x
2
;
.
.
.
;
x
n
)
w=(w_1;w_2;...;w_n), x=(x_1;x_2;...;x_n)
w=(w1?;w2?;...;wn?),x=(x1?;x2?;...;xn?),w 和 b 经过学习后,模型就可以确定。当自变量数量为 1 时,上述线性模型即为平面下的直线方程:
y
=
w
x
+
b
y=wx+b
y=wx+b
线性模型形式简单、易于建模,却蕴含着机器学习中一些重要的基本思想。许多功能强大的非线性模型可以在线性模型基础上引入层级结构或高维映射而得。此外,由于
w
w
w直观表达了各属性在预测中的重要性,因此线性模型具有很好的可解释性。例如,判断一个西瓜是否为好瓜,可以用如下表达式来判断:
f 好瓜 ( x ) = 0.2 x 色泽 + 0.5 x 根蒂 + 0.3 x 敲声 + 1 f_{好瓜}(x) = 0.2x_{色泽} + 0.5x_{根蒂} + 0.3x_{敲声} + 1 f好瓜?(x)=0.2x色泽?+0.5x根蒂?+0.3x敲声?+1
上述公式可以解释为,一个西瓜是否为好瓜,可以通过色泽、根蒂、敲声等因素共同判断,其中根蒂最重要(权重最高),其次是敲声和色泽。
3. 模型训练
在二维平面中,给定两点可以确定一条直线。但在实际工程中,可能有很多个样本点,无法找到一条直线精确穿过所有样本点,只能找到一条与样本”足够接近“或”距离足够小“的直线,近似拟合给定的样本。如下图所示:
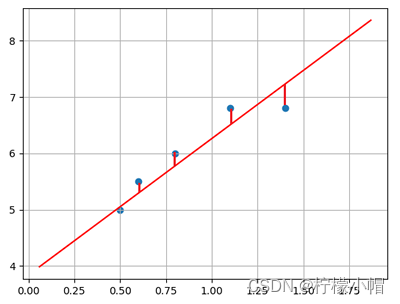
如何确定直线到所有样本足够近呢?可以使用损失函数来进行度量。
3.1 损失函数
损失函数用来度量真实值(由样本中给出)和预测值(由模型算出)之间的差异。损失函数值越小,表明模型预测值和真实值之间差异越小,模型性能越好;损失函数值越大,模型预测值和真实值之间差异越大,模型性能越差。在回归问题中,均方差是常用的损失函数,其表达式如下所示:
E = 1 2 ∑ i = 1 n ( y ? y ′ ) 2 E = \frac{1}{2}\sum_{i=1}^{n}{(y - y')^2} E=21?i=1∑n?(y?y′)2
其中,y 为模型预测值,y’为真实值。均方差具有非常好的几何意义,对应着常用的欧几里得距离(简称欧式距离)。线性回归的任务是要寻找最优线性模型,是的损失函数值最小,即:
( w ? , b ? ) = a r g m i n 1 2 ∑ i = 1 n ( y ? y ′ ) 2 = a r g m i n 1 2 ∑ i = 1 n ( y ′ ? w x i ? b ) 2 (w^*, b^*) = arg min \frac{1}{2}\sum_{i=1}^{n}{(y - y')^2} \\ = arg min \frac{1}{2}\sum_{i=1}^{n}{(y' - wx_i - b)^2} (w?,b?)=argmin21?i=1∑n?(y?y′)2=argmin21?i=1∑n?(y′?wxi??b)2
基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。线性回归中,最小二乘法就是试图找到一条直线,是所有样本到直线的欧式距离之和最小。可以将损失函数对 w 和 b 分别求导,得到损失函数的导函数,并令导函数为 0 即可得到 w 和 b 的最优解。
PS:机器学习主方向:
-
找到拟合当前数据的最优的模型
-
寻找最优的模型参数
-
使用梯度下降求损失函数的极小值
3.2 梯度下降法
3.2.1 为什么使用梯度下降
在实际计算中,通过最小二乘法求解最优参数有一定的问题:
(1)最小二乘法需要计算逆矩阵,有可能逆矩阵不存在;
(2)当样本特征数量较多时,计算逆矩阵非常耗时甚至不可行。
所以,在实际计算中,通常采用梯度下降法来求解损失函数的极小值,从而找到模型的最优参数。
3.2.2 什么是梯度下降
梯度(gradient)是一个向量(矢量,有方向),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大。损失函数沿梯度相反方向收敛最快(即能最快找到极值点)。当梯度向量为零(或接近于零),说明到达一个极值点,这也是梯度下降算法迭代计算的终止条件。
这种按照负梯度不停地调整函数权值的过程就叫作“梯度下降法”。通过这样的方法,改变权重让损失函数的值下降得更快,进而将值收敛到损失函数的某个极小值。
通过损失函数,我们将“寻找最优参数”问题,转换为了“寻找损失函数最小值”问题。梯度下降法算法描述如下:
(1)损失是否足够小?如果不是,计算损失函数的梯度。
(2)按梯度的反方向走一小步,以缩小损失。
(3)循环到(1)。

梯度下降法中通过沿着梯度负方向不断调整参数,从而逐步接近损失函数极小值所在点。如下图所示:
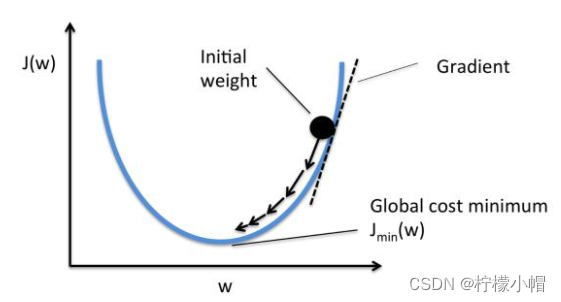
3.2.3 参数更新法则
在直线方程中,有两个参数需要学习, w 0 w_0 w0?和 w 1 w_1 w1?,梯度下降过程中,分别对这两个参数单独进行调整,调整法则如下:
w 0 = w 0 + Δ w 0 w 1 = w 1 + Δ w 1 w_0 = w_0 + \Delta w_0\\w_1 = w_1 + \Delta w_1 w0?=w0?+Δw0?w1?=w1?+Δw1?
Δ
w
0
\Delta w_0
Δw0?和
Δ
w
1
\Delta w_1
Δw1?可表示为:
Δ
w
0
=
?
η
Δ
l
o
s
s
Δ
w
0
Δ
w
1
=
?
η
Δ
l
o
s
s
Δ
w
1
\Delta w_0 = -\eta \frac{\Delta loss}{\Delta w_0}\\\Delta w_1 = -\eta \frac{\Delta loss}{\Delta w_1}\\
Δw0?=?ηΔw0?Δloss?Δw1?=?ηΔw1?Δloss?
其中,
η
\eta
η称为学习率,
Δ
l
o
s
s
Δ
w
i
\frac{\Delta loss}{\Delta w_i}
Δwi?Δloss?为梯度(即损失函数关于参数
w
i
w_i
wi?的偏导数)。损失函数表达式为:
l
o
s
s
=
1
2
∑
(
y
?
y
′
)
2
=
1
2
∑
(
(
y
?
(
w
0
+
w
1
x
)
)
2
)
loss =\frac{1}{2}\sum(y - y')^2 = \frac{1}{2}\sum((y-(w_0+w_1x))^2)
loss=21?∑(y?y′)2=21?∑((y?(w0?+w1?x))2)
对损失函数求导(求导过程见补充知识),可得 w 0 , w 1 w_0, w_1 w0?,w1?的偏导数为:
Δ l o s s Δ w 0 = ∑ ( ( y ? y ′ ) ( ? 1 ) ) = ? ∑ ( y ? y ′ ) Δ l o s s Δ w 1 = ∑ ( ( y ? y ′ ) ( ? x ) ) = ? ∑ ( x ( y ? y ′ ) ) \frac{\Delta loss}{\Delta w_0} = \sum((y - y')(-1)) = -\sum(y - y')\\\frac{\Delta loss}{\Delta w_1} = \sum((y - y')(-x)) = -\sum(x(y - y')) Δw0?Δloss?=∑((y?y′)(?1))=?∑(y?y′)Δw1?Δloss?=∑((y?y′)(?x))=?∑(x(y?y′))
PS:超参数
- 在构建模型时,需要设定一系列的参数,而这些参数可以决定模型的精度。超参数的设定一般取决于经验。
4. 实现线性回归
4.1 自己编码实现
以下是实现线性回归的代码:
# 线性回归示例
import numpy as np
import matplotlib.pyplot as mp
from mpl_toolkits.mplot3d import axes3d
import sklearn.preprocessing as sp
# 训练数据集
train_x = np.array([0.5, 0.6, 0.8, 1.1, 1.4]) # 输入集
train_y = np.array([5.0, 5.5, 6.0, 6.8, 7.0]) # 输出集
n_epochs = 1000 # 迭代次数
lrate = 0.01 # 学习率
epochs = [] # 记录迭代次数
losses = [] # 记录损失值
w0, w1 = [1], [1] # 模型初始值
for i in range(1, n_epochs + 1):
epochs.append(i) # 记录第几次迭代
y = w0[-1] + w1[-1] * train_x # 取出最新的w0,w1计算线性方程输出
# 损失函数(均方差)
loss = (((train_y - y) ** 2).sum()) / 2
losses.append(loss) # 记录每次迭代的损失值
print("%d: w0=%f, w1=%f, loss=%f" % (i, w0[-1], w1[-1], loss))
# 计算w0,w1的偏导数
d0 = -(train_y - y).sum()
d1 = -(train_x * (train_y - y)).sum()
# 更新w0,w1
w0.append(w0[-1] - (d0 * lrate))
w1.append(w1[-1] - (d1 * lrate))
程序执行结果:
1 w0=1.00000000 w1=1.00000000 loss=44.17500000
2 w0=1.20900000 w1=1.19060000 loss=36.53882794
3 w0=1.39916360 w1=1.36357948 loss=30.23168666
4 w0=1.57220792 w1=1.52054607 loss=25.02222743
5 w0=1.72969350 w1=1.66296078 loss=20.71937337
......
996 w0=4.06506160 w1=2.26409126 loss=0.08743506
997 w0=4.06518850 w1=2.26395572 loss=0.08743162
998 w0=4.06531502 w1=2.26382058 loss=0.08742820
999 w0=4.06544117 w1=2.26368585 loss=0.08742480
1000 w0=4.06556693 w1=2.26355153 loss=0.08742142
可以给数据加上可视化,让结果更直观.添加如下代码:
###################### 训练过程可视化 ######################
# 训练过程可视化
## 损失函数收敛过程
w0 = np.array(w0[:-1])
w1 = np.array(w1[:-1])
mp.figure("Losses", facecolor="lightgray") # 创建一个窗体
mp.title("epoch", fontsize=20)
mp.ylabel("loss", fontsize=14)
mp.grid(linestyle=":") # 网格线:虚线
mp.plot(epochs, losses, c="blue", label="loss")
mp.legend() # 图例
mp.tight_layout() # 紧凑格式
## 显示模型直线
pred_y = w0[-1] + w1[-1] * train_x # 根据x预测y
mp.figure("Linear Regression", facecolor="lightgray")
mp.title("Linear Regression", fontsize=20)
mp.xlabel("x", fontsize=14)
mp.ylabel("y", fontsize=14)
mp.grid(linestyle=":")
mp.scatter(train_x, train_y, c="blue", label="Traing") # 绘制样本散点图
mp.plot(train_x, pred_y, c="red", label="Regression")
mp.legend()
# 显示梯度下降过程(复制粘贴即可,不需要编写)
# 计算损失函数曲面上的点 loss = f(w0, w1)
arr1 = np.linspace(0, 10, 500) # 0~9间产生500个元素的均匀列表
arr2 = np.linspace(0, 3.5, 500) # 0~3.5间产生500个元素的均匀列表
grid_w0, grid_w1 = np.meshgrid(arr1, arr2) # 产生二维矩阵
flat_w0, flat_w1 = grid_w0.ravel(), grid_w1.ravel() # 二维矩阵扁平化
loss_metrix = train_y.reshape(-1, 1) # 生成误差矩阵(-1,1)表示自动计算维度
outer = np.outer(train_x, flat_w1) # 求外积(train_x和flat_w1元素两两相乘的新矩阵)
# 计算损失:((w0 + w1*x - y)**2)/2
flat_loss = (((flat_w0 + outer - loss_metrix) ** 2).sum(axis=0)) / 2
grid_loss = flat_loss.reshape(grid_w0.shape)
mp.figure('Loss Function')
ax = mp.gca(projection='3d')
mp.title('Loss Function', fontsize=14)
ax.set_xlabel('w0', fontsize=14)
ax.set_ylabel('w1', fontsize=14)
ax.set_zlabel('loss', fontsize=14)
ax.plot_surface(grid_w0, grid_w1, grid_loss, rstride=10, cstride=10, cmap='jet')
ax.plot(w0, w1, losses, 'o-', c='orangered', label='BGD', zorder=5)
mp.legend(loc='lower left')
mp.show()
数据可视化结果如下图所示:
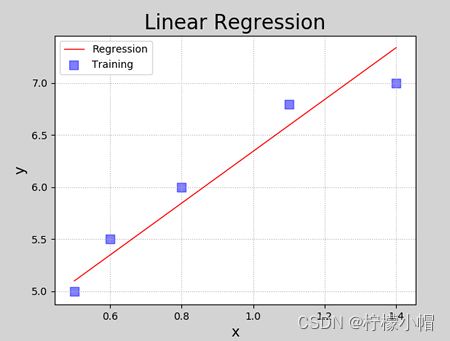
回归得到的线性模型
回归得到的线性模型
回归得到的线性模型
?
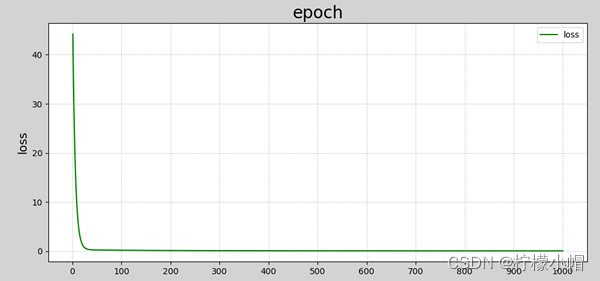
损失函数收敛过程
损失函数收敛过程
损失函数收敛过程
?
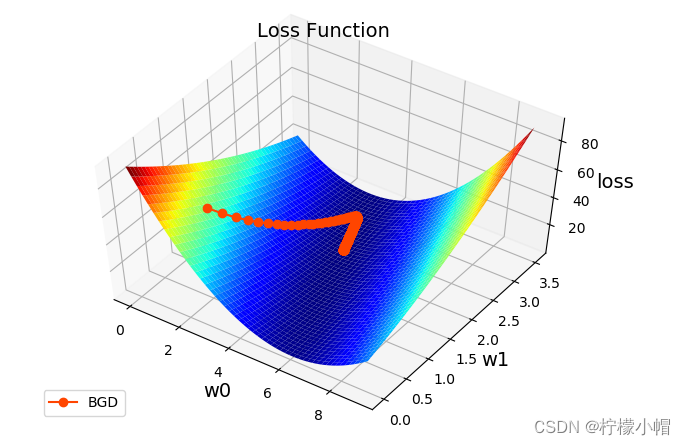
?
梯度下降过程
梯度下降过程
梯度下降过程
?
4.2 通过 sklearn API 实现
同样,可以使用 sklearn 库提供的 API 实现线性回归。代码如下:
# 利用LinearRegression实现线性回归
import numpy as np
import sklearn.linear_model as lm # 线性模型# 线性模型
import sklearn.metrics as sm # 模型性能评价模块
import matplotlib.pyplot as mp
?
train_x = np.array([[0.5], [0.6], [0.8], [1.1], [1.4]]) # 输入集
train_y = np.array([5.0, 5.5, 6.0, 6.8, 7.0]) # 输出集
?
# 创建线性回归器
model = lm.LinearRegression()
# 用已知输入、输出数据集训练回归器
model.fit(train_x, train_y)
# 输入数据x:必须是二维
# 输出数据y:最好是一维的
# 根据训练模型预测输出
pred_y = model.predict(train_x)
print("coef_:", model.coef_) # 系数
print("intercept_:", model.intercept_) # 截距
# 可视化回归曲线
mp.figure('Linear Regression', facecolor='lightgray')
mp.title('Linear Regression', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
# 绘制样本点
mp.scatter(train_x, train_y, c='blue', alpha=0.8, s=60, label='Sample')
# 绘制拟合直线
mp.plot(train_x, # x坐标数据
pred_y, # y坐标数据
c='orangered', label='Regression')
mp.legend()
mp.show()
执行结果:
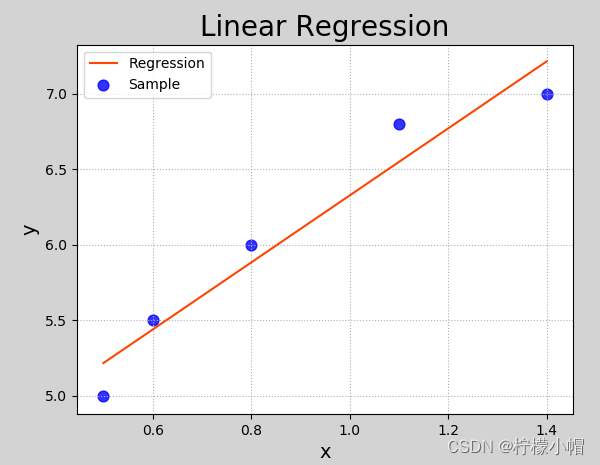
5. 模型评价指标
(1)平均绝对误差(Mean Absolute Deviation):单个观测值与预测值的偏差的绝对值的平均;
(2)均方误差:单个样本到平均值差值的平方平均值;
(3)MAD(中位数绝对偏差):与数据中值绝对偏差的中值;
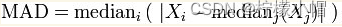
(4)R2 决定系数:趋向于 1,模型越好;趋向于 0,模型越差。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!