图解系列--密钥，随机数，应用技术

密钥

1.生成密钥
1.1.用随机数生成密钥
密码学用途的伪随机数生成器必须是专门针对密码学用途而设计的。
1.2.用口令生成密钥
一般都是将口令输入单向散列函数，然后将得到的散列值作为密钥使用。
在使用口令生成密钥时，为了防止字典攻击，需要在口令上面附加一串称为盐的随机数，然后再将其输入单向散列函数。这种方法称为“基于口令的密码” 。
1.3.更新密钥
有一种提高通信机密性的技术被称为密钥更新，这种方法就是在使用共享密钥进行通信的过程中，定期改变密钥。
在更新密钥时，发送者和接收者使用单向散列函数计算当前密钥的散列值，并将这个散列值用作新的密钥。简单说，就是用当前密钥的散列值作为下一个密钥。
1.4.保存密钥
会话密钥在通信过程中仅限使用一次，因此我们不需要保存这种密钥。然而，当密钥需要重复使用时，就必须要考虑保存密钥的问题了。
1.5.Diffie-Hellman密钥交换
使用这种算法，通信双方仅通过交换一些可以公开的信息就能够生成出共享的秘密数字，而这一秘密数字就可以被用作对称密码的密钥。实际上双方并没有真正交换密钥，而是通过计算生成出了一个相同的共享秘钥。
1.5.1.Diffie-Hellman 密钥交换的步骤

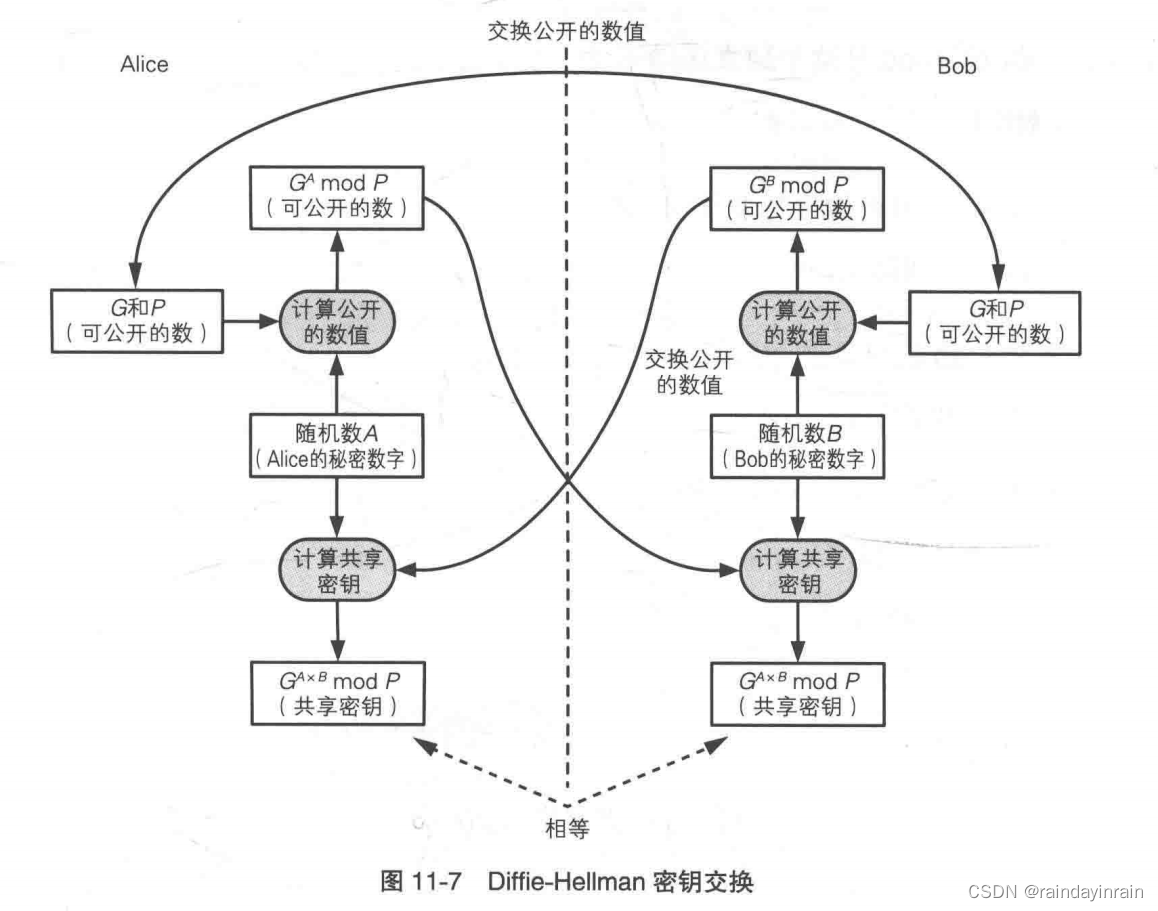
(1).Alice向Bob发送两个质数P和G
P必须是一个非常大的质数，而G则是一个和P相关的数，称为生成元。P和G不需要保密，被窃听者Eve获取也没关系。
(2).Alice生成一个随机数A
A 是一个1 ~ P - 2 之间的整数。这个数是一个只有Alice知道的秘密数字。
(3).Bob生成一个随机数B
B是一个1 ~ P - 2 之间的整数。这个数是一个只有Bob知道的秘密数字。
(4).Alice 将$G^{A}modP$这个数发送给Bob
这个数让Eve知道也没关系。
(5).Bob 将$G^{B}modP$这个数发送给Alice
这个数让Eve知道也没关系。
(6).Alice用Bob发过来的数计算A次方并求mod P
Alice计算的密钥=$(G^{B}modP{)}^{A}modP$=$(G^{B?A}modP)$
(7).Bob用Alice发过来的数计算B次方并求mod P
Bob计算的密钥=$(G^{A}modP{)}^{B}modP$=$(G^{B?A}modP)$

1.5.2.Eve能计算出密钥吗
在步骤(1)~(7)中，双方交换的数字(即能够被窃听者Eve知道的数字) 一共有4个：$P、G、G^{A}modP和G^{B}modP$。根据这4个数字计算出Alice和Bob的共享密钥$(G^{A\times B}modP)$是非常困难的。

如果仅仅是$G^A$的话，要计算出A并不难，然而根据$G^{A}modP$计算出A 的有效算法到现在还没有出现，这个问题称为有限域的离散对数问题。而有限域的离散对数问题的复杂度正是支撑 Diffie-Hellman 密钥交换算法的基础。

1.5.3.生成元的意义

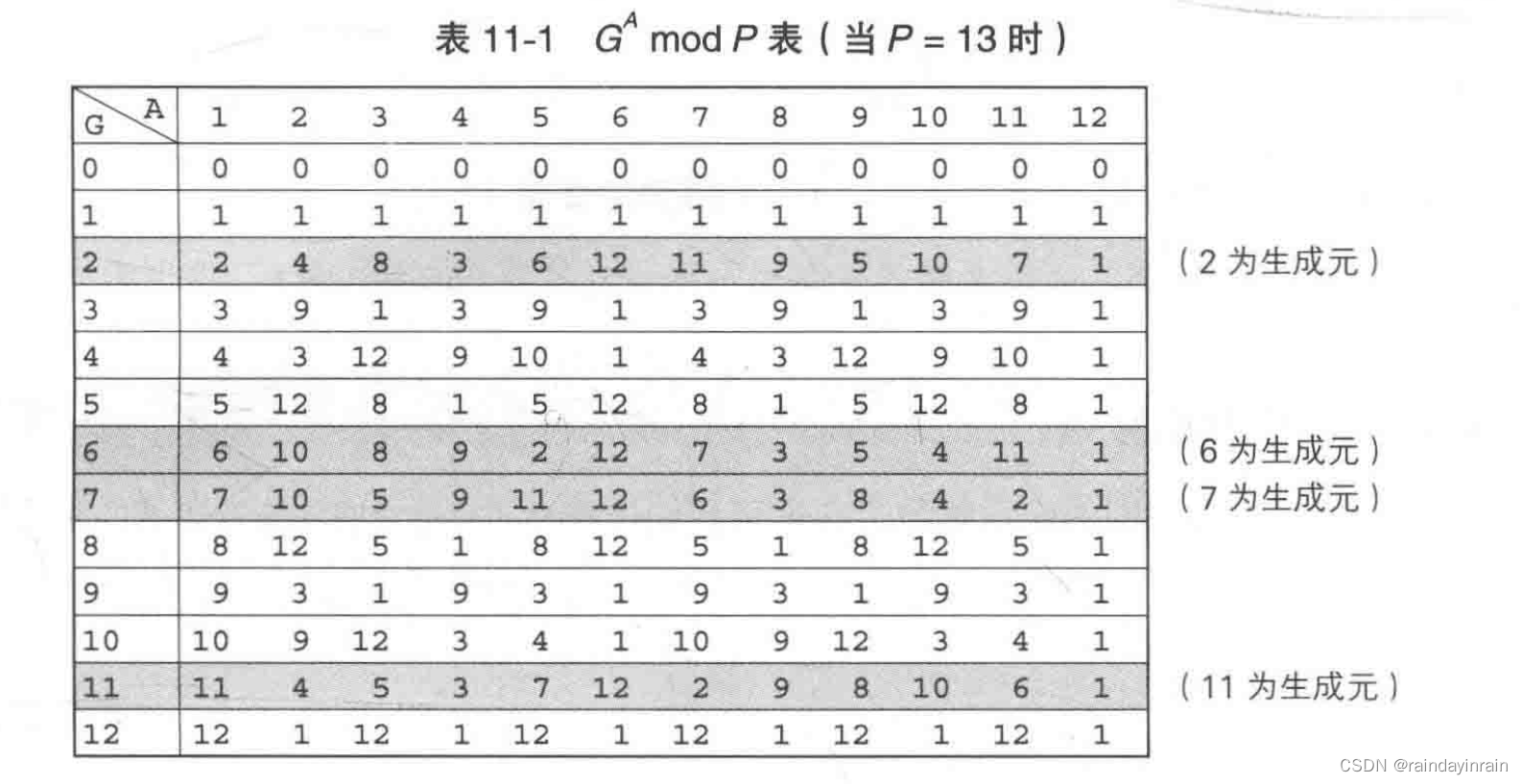
我们可以发现$2^1$到$2^{12}$的值(共12个)全都不一样。也就是说，2的乘方结果中出现了1到12的全部整数。由于2具备上述性质，因此称为13的生成元。同样地，6、7和11也是生成元。

也就是说，P的生成元的乘方结果与1 ~ P - 1 中的数字是一一对应的。正是因为具有这样一一对应的关系，Alice才能够从1~ P-2的范围中随机选择一个数字(之所以不能选择P-1，是因为$G^{P?1}modP$的值一定是等于1的)。

1.6.基于口令的密码
基于口令的密码就是一种根据口令生成密钥并用该密钥进行加密的方法。其中加密和解密使用同一个密钥。
1.6.1. PBE加密

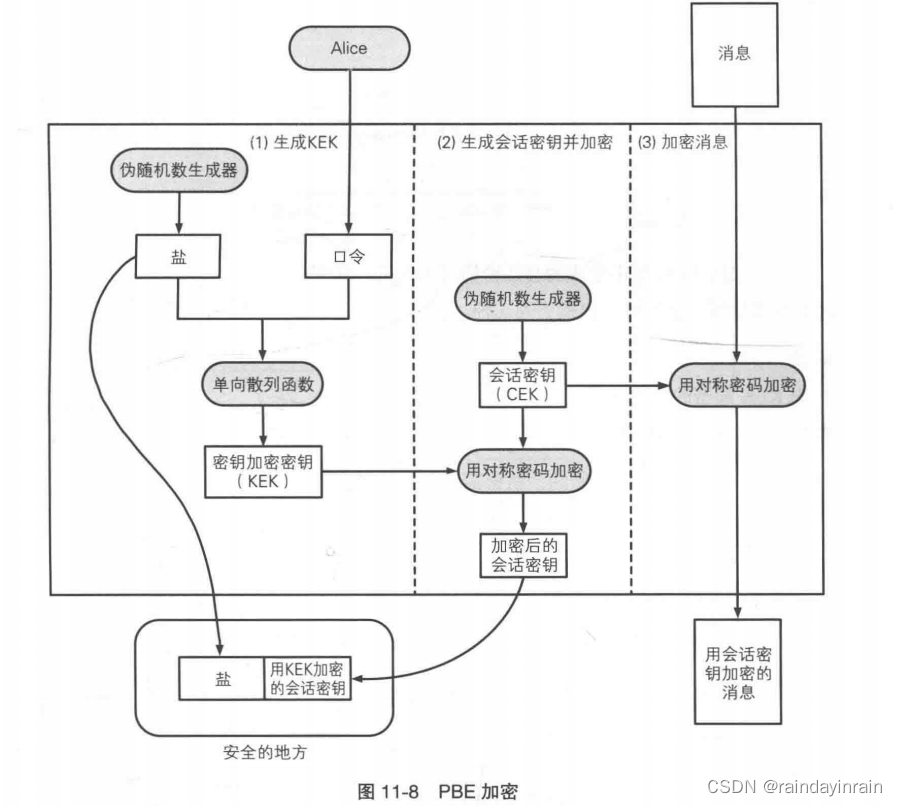
(1).生成KEK
首先，伪随机数生成器会生成一个被称为盐的随机数。将盐和Alice输入的口令一起输入单向散列函数，得到的散列值就是用来加密密钥的密钥(KEK)。
(2).生成会话密钥并加密
我们使用伪随机数生成器生成会话密钥。会话密钥是用来加密消息的密钥 (CEK)。
会话密钥需要用刚才步骤(1)中生成的KEK进行加密，并和盐一起保存在安全的地方。会话密钥加密之后，KEK就会被丢弃，因为KEK没有必要保存下来，只要通过盐和口令就可以重建 KEK。
(3).加密消息
(4).保存
“盐”和“用KEK加密的会话密钥”需要保存在安全的地方。

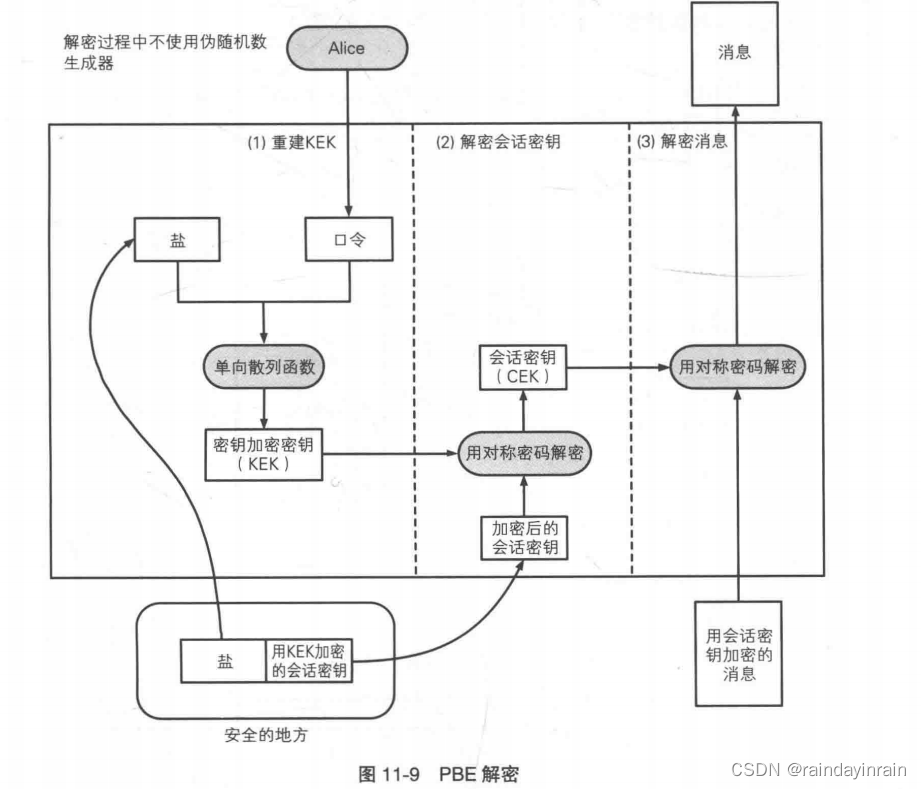
1.6.2.PBE解密
(1).重建KEK
我们将之前保存下来的盐，和Alice输入的口令一起输入单向散列函数。这个计算过程和生成 KEK时的计算过程是一样的，因此所得到的散列值就是KEK。
(2).解密会话密钥
我们获取之前保存下来的“用KEK加密的会话密钥”，用步骤(1)中恢复的KEK进行解密。这一步我们可以得到会话密钥。
(3).解密消息

1.6.3.盐的作用
盐是用来防御字典攻击的。字典攻击是一种事先进行计算并准备好候选密钥列表的方法。

我们假设在生成KEK的时候没有加盐。那么主动攻击者 Mallory 就可以根据字典数据（各种可能口令）事先生成大量的候选KEK。
在这里，事先是很重要的一点。这意味着Mallory可以在窃取到加密的会话密钥之前，就准备好了大量的候选KEK 。当 Mallory 窃取加密的会话密钥后，就需要尝试将它解密，这时只要利用事先生成的候选KEK，就能够大幅缩短尝试的时间，这就是字典攻击。

如果在生成KEK 时加盐，则盐的长度越大，候选KEK的数量也会随之增大，事先生成候选KEK 就会变得非常困难。加盐之后，候选KEK的数量会变得非常巨大。

1.6.4.口令的作用
在使用基于口令的密码时，需要将盐和加密后的CEK通过物理方式进行保护。例如可以将盐和加密后的CEK保存到存储卡中随身携带。

1.6.5.通过拉伸来改良PBE
将单向散列函数进行多次迭代的方法称为拉伸。

1.6.6.如何生成安全的口令
(1).使用只有自己才能知道的信息
(2).将多个不同的口令分开使用
(3).有效利用笔记
用伪随机数生成器生成一个随机的字符串作为口令，然后将口令记下来保存在安全的地方。换言之， 应该将笔记与物理的钥匙同等对待。仅将口令的一部分写下来的方法也是非常有效的。
(4).理解口令的局限性
(5).使用口令生成和管理工具

随机数

1.随机数的性质
对随机数的性质进行分类
(1).随机性——不存在统计学偏差，是完全杂乱的数列
(2).不可预测性——不能从过去的数列推测出下一个出现的数
(3).不可重现性——除非将数列本身保存下来，否则不能重现相同的数列

1.1.随机性
看起来杂乱无章

1.2.不可预测性
无法通过历史数据预测未来

1.3.不可重现性
无法重现和某一随机数列完全相同的数列的性质。如果除了将随机 数列本身保存下来以外，没有其他方法能够重现该数列，则我们就说该随机数列具备不可重现性。

软件只能生成伪随机数列，这是因 为运行软件的计算机本身仅具备有限的内部状态。首次出现重复之前的数列长度称为周期，对于软件所生成的数列，其周期必定是有限的。

要生成具备不可重现性的随机数列，需要从不可重现的物理现象中获取信息，根据从这些硬件中所获取的信息而生成的数列， 一般可以认为是具备不可重现性的随机 数列。

2.伪随机数生成器
通过硬件生成的随机数列，是根据传感器收集的热量、声音的变化等事实上无法预测和重现的自然现象信息来生成的。像这样的硬件设备就称为随机数生成器。可以生成随机数的软件则称为伪随机数生成器。因为仅靠软件无法生成真随机数，因此要加上一个“伪”字。

2.1.伪随机数生成器的结构

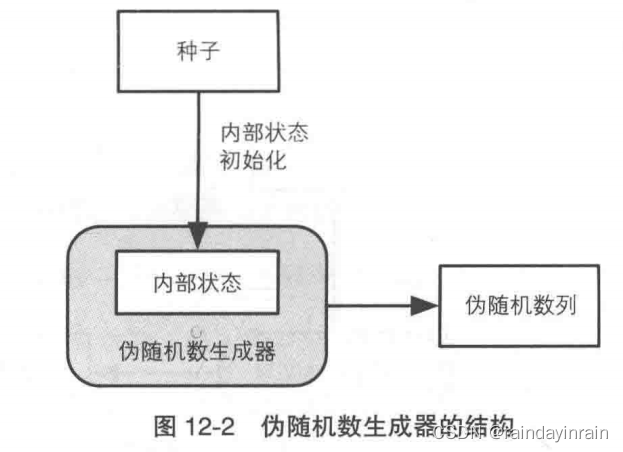
(1).伪随机数生成器的内部状态
将根据内部状态计算伪随机数的方法和改变内部状态的方法组合起来，就是伪随机数生成的算法。
(2).伪随机数生成器的种子
伪随机数的种子是用来对伪随机数生成器的内部状态进行初始化的。
伪随机数生成器是公开的，但种子是需要自己保密的，这就好像密码算法是公开的，但密钥只 能自己保密。

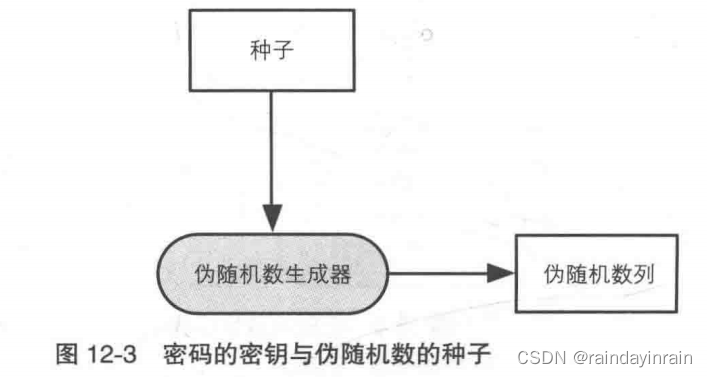
3.具体的伪随机数生成器
3.1.线性同余法
线性同余法是一种使用很广泛的伪随机数生成器算法。然而， 它并不能用于密码技术。
假设我们要生成的伪随机数列为$R_0、R_1、R_2\dots$。首先我们根据伪随机数的种子，用下列公式计算第一个伪随机数$R_0$。
第一个伪随机数 $R_0=(A\times 种子+C)modM$。在这里，A、C、M都是常量，且A和C需要小于M。
接下来，我们根据R。用相同的公式计算下一个伪随机数R。$R_1=(A\times R_0+C)modM$。
接下来我们再用同样的方法，根据当前的伪随机数$R_n$，来计算下一个伪随机数$R_{n+1}$。$R_{n+1}=(A\times R_n+C)modM$。

简而言之，线性同余法就是将当前的伪随机数值乘以A 再加上C， 然后将除以M得到的余数作为下一个伪随机数。在线性同余法中，最近一次生成的伪随机数的值就是内部状态，伪随机数的种子被用来对内部状态进行初始化。

线性同余法不具备不可预测性，因此不可以将线性同余法用于密码技术。

3.2.单向散列函数法
使用单向散列函数(如 SHA-1)可以编写出能够生成具备不可预测性的伪随机数列(即强伪随机数)的伪随机数生成器。

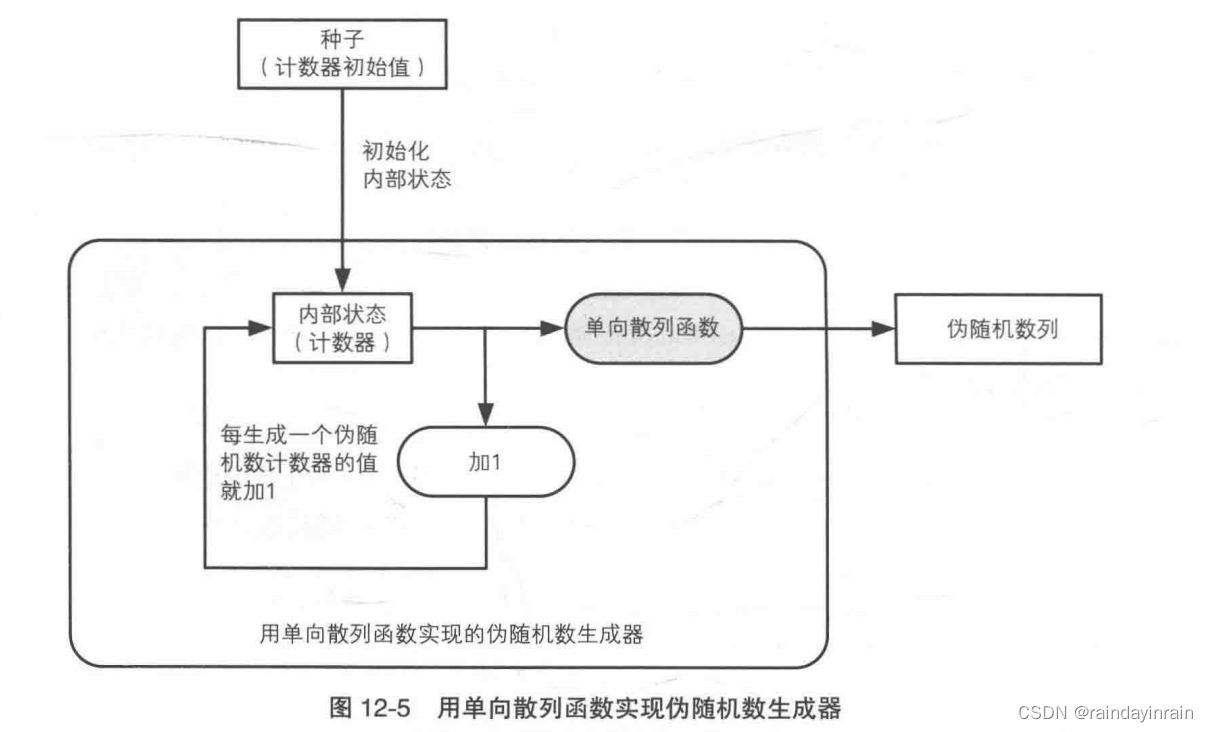
这种伪随机数生成器的工作方式如下。
(1).用伪随机数的种子初始化内部状态(计数器)。
(2).用单向散列函数计算计数器的散列值。
(3).将散列值作为伪随机数输出。
(4).计数器的值加1。
(5).根据需要的伪随机数数量重复(2)~(4)的步骤。

单向散列函数的单向性是支撑伪随机数生成器不可预测性的基础。

3.3.密码法
我们可以使用密码来编写能够生成强伪随机数的伪随机数生成器。既可以使用AES等对称密码，也可以使用RSA等公钥密码。

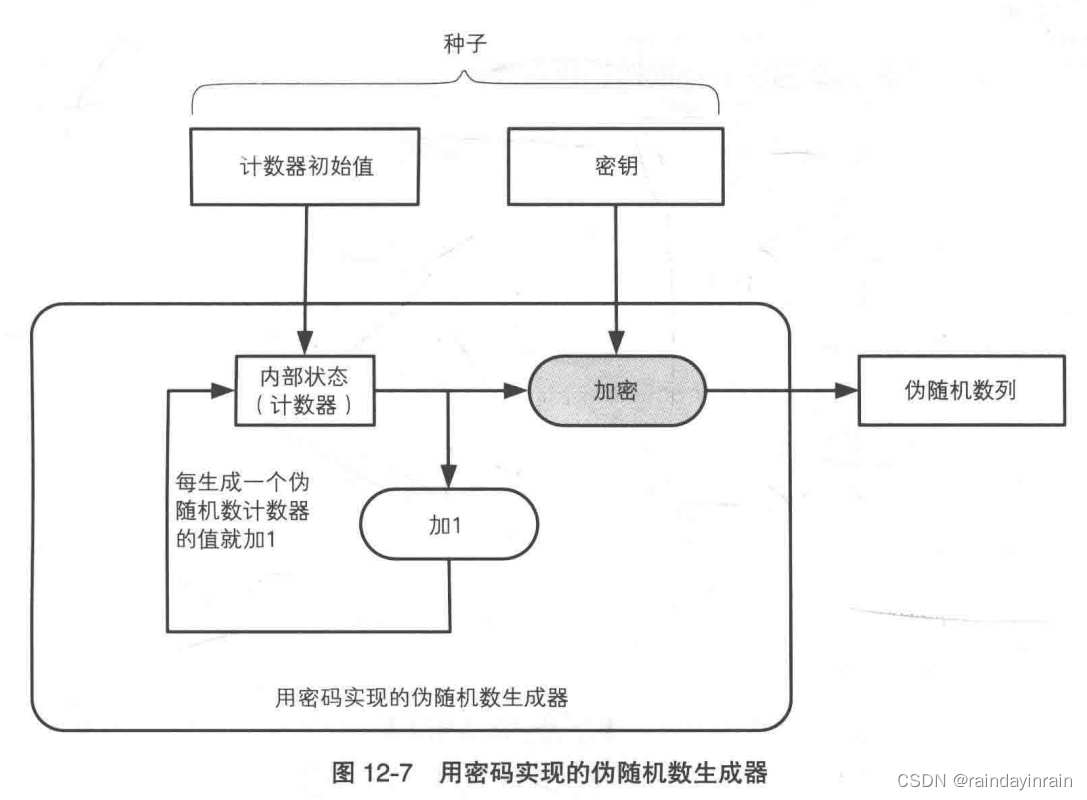
(1).初始化内部状态(计数器)。
(2).用密钥加密计数器的值。
(3).将密文作为伪随机数输出。
(4).计数器的值加1。
(5).根据需要的伪随机数数量重复(2)~(4)的步骤。

密码的机密性是支撑伪随机数生成器不可预测性的基础。

3.4.ANSI X9.17
ANSI X9.17伪随机数生成器的结构如图12-8所示。

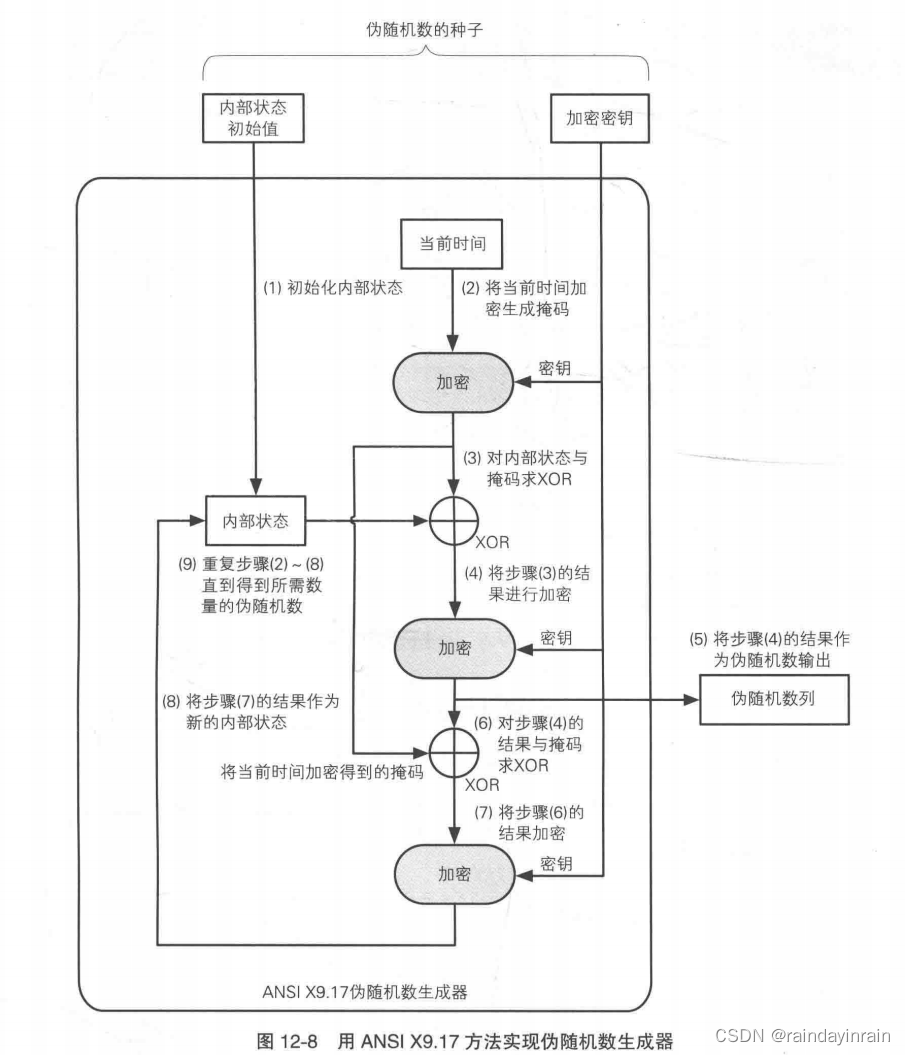
(1).初始化内部状态。
(2).将当前时间加密生成掩码。
(3).对内部状态与掩码求 XOR。
(4).将步骤(3)的结果进行加密。
(5).将步骤(4)的结果作为伪随机数输出。
(6).对步骤(4)的结果与掩码求xOR。
(7).将步骤(6)的结果加密。
(8).将步骤(7)的结果作为新的内部状态。
(9).重复步骤(2)~(8)直到得到所需数量的伪随机数。

4.对伪随机数生成器的攻击
4.1.对种子进行攻击
如果攻击者知道了伪随机数的种子，那么他就能够知道这个伪随机数生成器所生成的全部伪随机数列。
要避免种子被攻击者知道，我们需要使用具备不可重现性的真随机数作为种子。

4.2.对随机数池进行攻击
我们一般不会到了需要的时候才当场生成真随机数，而是会事先在一个名为随机数池的文件中积累随机比特序列。当密码软件需要伪随机数的种子时，可以从这个随机数池中取出所需长度的随机比特序列来使用。
随机数池的内容不可以被攻击者知道，否则伪随机数的种子就有可能被预测出来。

5.总结
在密码技术中使用的伪随机数生成器，是以具备不可重现性的真随机数作为伪随机数的种子，来生成具备不可预测性的强伪随机数的。

SSL/TLS

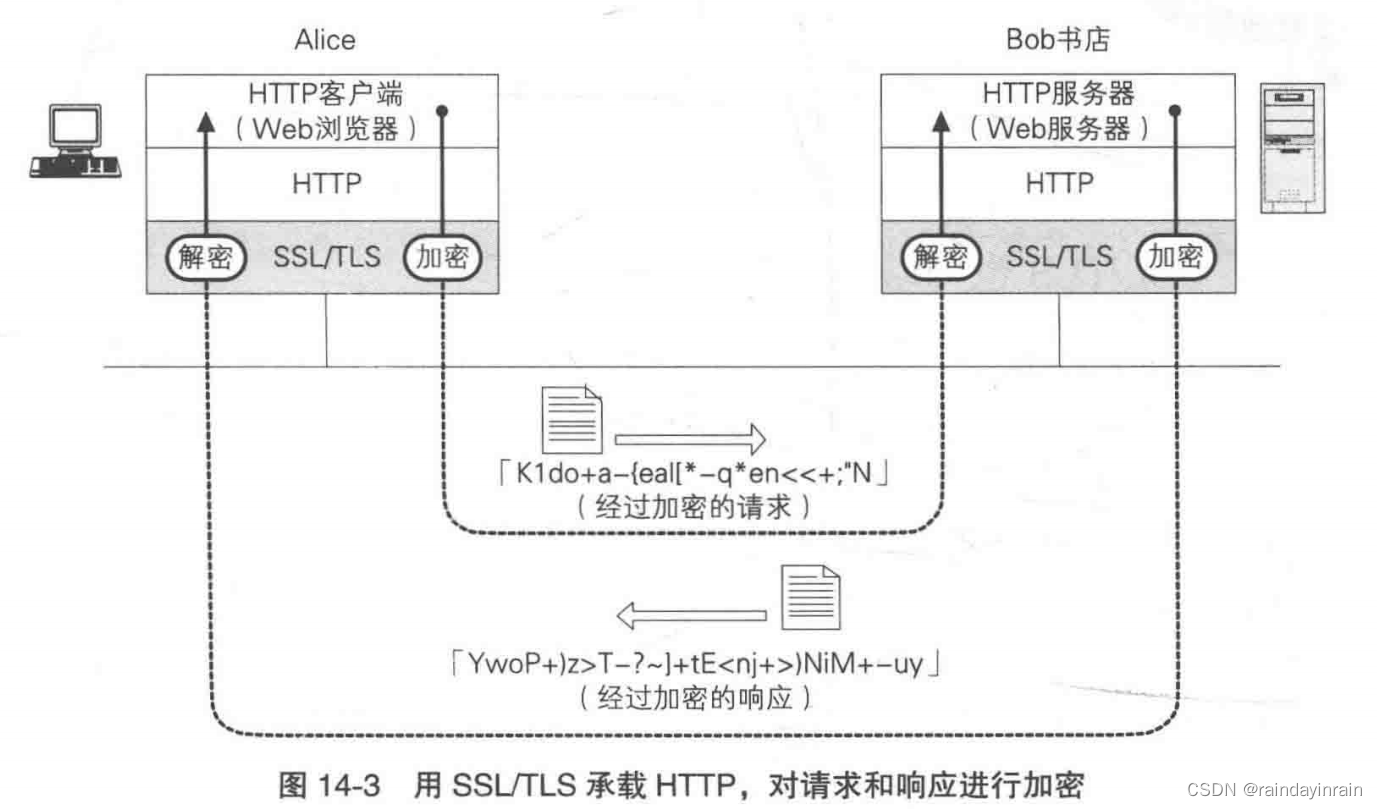
1.SSL/TLS
以下内容是基于TLS 1.2。
1.1.层次化的协议
TLS协议是由TLS记录协议和TLS握手协议这两层协议叠加而成的。位于底层的TLS记录协议负责进行加密，而位于上层的TLS握手协议则负责除加密以外的其他各种操作。

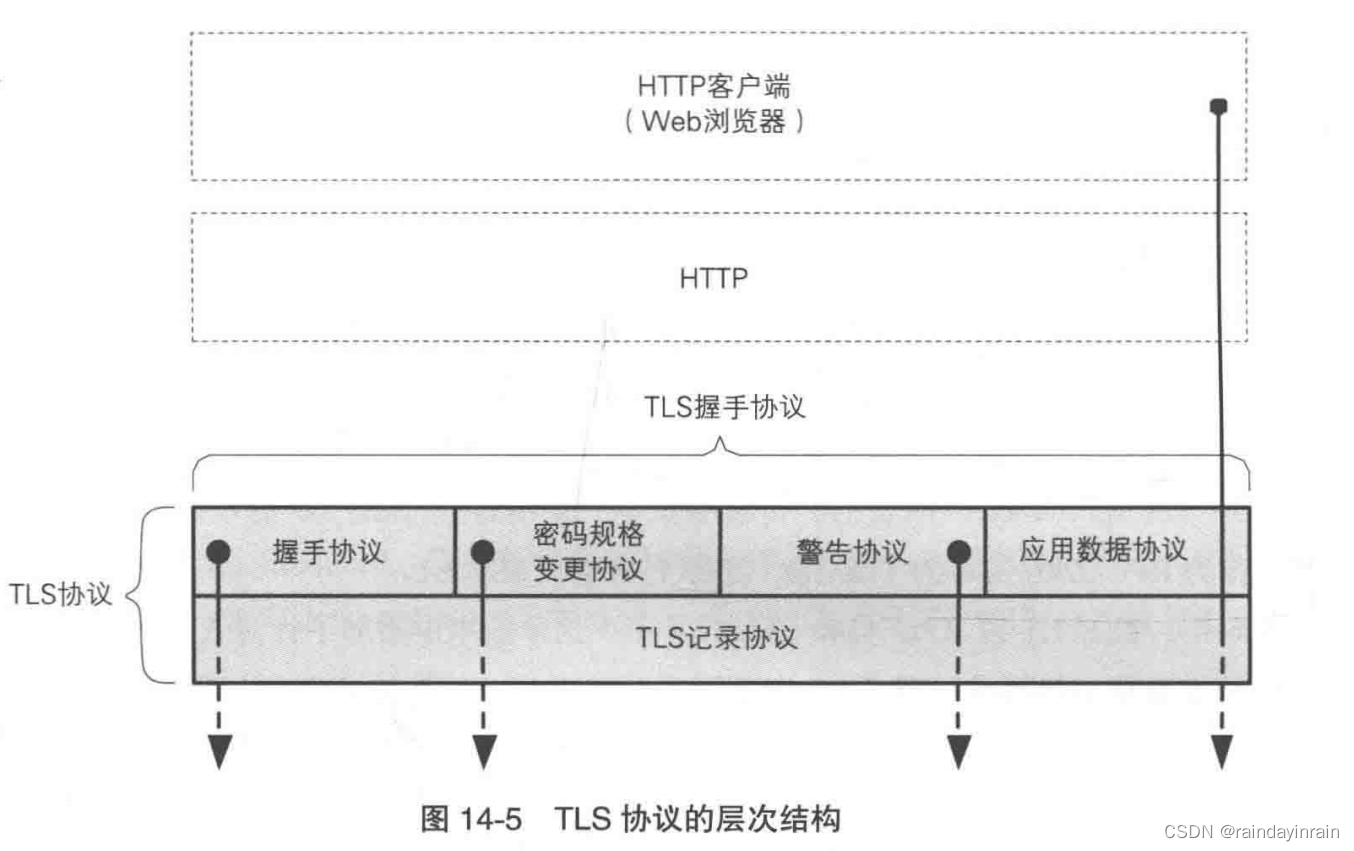
1.1.1.TLS记录协议
TLS 记录协议负责消息的压缩、加密以及数据的认证。
消息被分割成多个较短的片段(fragment), 然后分别对每个片段进行压缩。压缩算 法需要与通信对象协商决定。
经过压缩的片段会被加上消息认证码，与此同时，为了防止重放攻击，在计算消息认证码时，还加上了片段的编号。

单向散列函数的算法，以及消息认证码所使用的共享密钥都需要与通信对象协商决定。
经过压缩的片段再加上消息认证码会一起通过对称密码进行加密。
加密使用CBC模式，CBC 模式的初始化向量(IV)通过主密码生成，而对称密码的算法以及共享密钥需要与通信对象协商决定。
上述经过加密的数据再加上由数据类型、版本号、压缩后的长度组成的报头就是最终的报文数据。

1.1.2.TLS 握手协议
TLS 握手协议分为下列4个子协议：握手协议、密码规格变更协议、警告协议和应用数据协议。

(1).握手协议
在客户端和服务器之间协商决定密码算法和共享密钥。基于证书的认证操作也在这个协议中完成。
为了便于大家理解，我们以人类对话的形式来描述客户端和服务器之间的信息交换。
_1.ClientHello (客户端 --> 服务器)
客户端：你好。我能理解的密码套件有RSA/3DES、DSS/AES, 请问我们使用哪一种 密码套件进行通信呢?
信息中还包含：
●可用的版本号
●当前时间
●客户端随机数
●会话 ID
●可用的密码套件清单
●可用的压缩方式清单

_2.ServerHello(客户端 <-- 服务器)
服务器：你好。我们就用RSA/3DES来进行通信吧。
信息中还包含：
●使用的版本号
●当前时间
●服务器随机数
●会话 ID
●使用的密码套件
●使用的压缩方式

_3.Certificate (客户端 <-- 服务器) – 非必须
服务器：好，这是我的证书。
信息中还包含：
●证书清单

证书清单是一组X.509v3证书序列，首先发送的是服务器(发送方)的证书，然后会按顺序发送对服务器证书签名的认证机构的证书。
客户端会对服务器发送过来的证书进行验证。验证通过后可以从证书中获取可信的服务端公钥。

_4.ServerKeyExchange(客户端 <-- 服务器) – 非必须
服务器：我们用这些信息来进行密钥交换吧。
当Certificate消息不足以满足需求时，服务器会通过ServerKeyExchange消息向客户端发送 一些必要信息。具体所发送的信息内容会根据所使用的密码套件而有所不同。解决密钥配送可以用公钥（证书），也可用密钥交换技术。

_5.CertificateRequest (客户端 <-- 服务器)
服务器：对了，请给我看一下你的证书吧。
信息中包含：
●服务器能够理解的证书类型清单
●服务器能够理解的认证机构名称清单

_6.ServerHelloDone(客户端 <-- 服务器)
服务器：问候到此结束。

_7.Certificate(客户端 --> 服务器)
客户端：这是我的证书。

服务器读取客户端的证书并进行验证。

_8.ClientKeyExchange(客户端 --> 服务器)
客户端：这是经过加密的预备主密码。

预备主密码是由客户端生成的随机数，之后会被用作生成主密码的种 子。这个值会在使用服务器的公钥进行加密后发送给服务器。
根据预备主密码，服务器和客户端会计算出相同的主密码，然后再根据主密码生成下列比特序列(密钥素材)。
●对称密码的密钥
●消息认证码的密钥
●对称密码的CBC 模式中使用的初始化向量(IV)

_9.CertificateVerify(客户端 --> 服务器)
客户端：我确实是客户端证书的持有者本人。
客户端会计算“主密码”和“握手协议中传送的消息”的散列值，并加上自己的数字签名后发送给服务器。

_10.ChangeCipherSpec(客户端 --> 服务器)
客户端：好，现在我要切换密码了。

_11.Finished(客户端 --> 服务器)
客户端：握手协议到此结束。

_12.ChangeCipherSpec(客户端 <-- 服务器)
服务器：好，现在我要切换密码了。

_13.Finished(客户端 <-- 服务器)
服务器：握手协议到此结束。

_14.切换至应用数据协议
在此之后，客户端和服务器会使用应用数据协议和TLS 记录协议进行密码通信。 从结果来看，握手协议完成了下列操作。
●客户端获得了服务器的合法公钥，完成了服务器认证
●服务器获得了客户端的合法公钥，完成了客户端认证(当需要客户端认证时)
●客户端和服务器生成了密码通信中使用的共享密钥
●客户端和服务器生成了消息认证码中使用的共享密钥

服务器和客户端之间通过握手协议协商一致之后，就会相互发出信号来切换密码。负责 发出信号的就是下面要介绍的密码规格变更协议。

(2).密码规格变更协议
这个协议所发送的消息，大致相当于下面的对话。
客户端：好，我们按照刚才的约定切换密码吧。1、2、3!
当协议中途发生错误时，就会通过下面的警告协议传达给对方。
(3).警告协议
在发生错误时将错误传达给对方。 这个协议所发送的消息，大致相当于下面的对话。
服务器：刚才的消息无法正确解密哦!
如果没有发生错误，则会使用下面的应用数据协议来进行通信。
(4).应用数据协议
应用数据协议是将TLS上面承载的应用数据传达给通信对象的协议。

1.1.3.主密码
主密码是一个48字节(384比特)的数值。
(1).主密码的计算
主密码是客户端和服务器根据下列信息计算出来的。
●预备主密码
●客户端随机数
●服务器随机数
当使用RSA公钥密码时，客户端会在发送 ClientKeyExchange 消息时，将经过加密的预备主密码一起发送给服务器。
当使用 Diffie-Hellman密钥交换时，客户端会在发送ClientKeyExchange 消息时，将Diffie-Hellman的公开值一起发送给服务器。根据这个值，客户端和服务器会各自生成预备主密码。

当根据预备主密码计算主密码时，需要使用基于密码套件中定义的单项散列函数来实现的伪随机函数。

(2).主密码的目的
主密码用于生成下列6种信息。
●对称密码的密钥(客户端 --> 服务器)
●对称密码的密钥(客户端 <-- 服务器)
●消息认证码的密钥(客户端 --> 服务器)
●消息认证码的密钥(客户端 <-- 服务器)
●对称密码的CBC模式所使用的初始化向量(客户端 --> 服务器)
●对称密码的CBC模式所使用的初始化向量(客户端 <-- 服务器)

1.1.4.TLS 中使用的密码技术小结