【算法】递归、搜索与回溯算法

一. 名词解释

1. 递归

1.1 什么是递归？

递归就是函数自己调用自己

1.2 为什么会用到递归？

本质：我们在解决主问题时，会遇到和主问题相同的子问题，而子问题和主问题的解决方式一样，所以必定会出现函数自己调用自己（即递归）的情况。

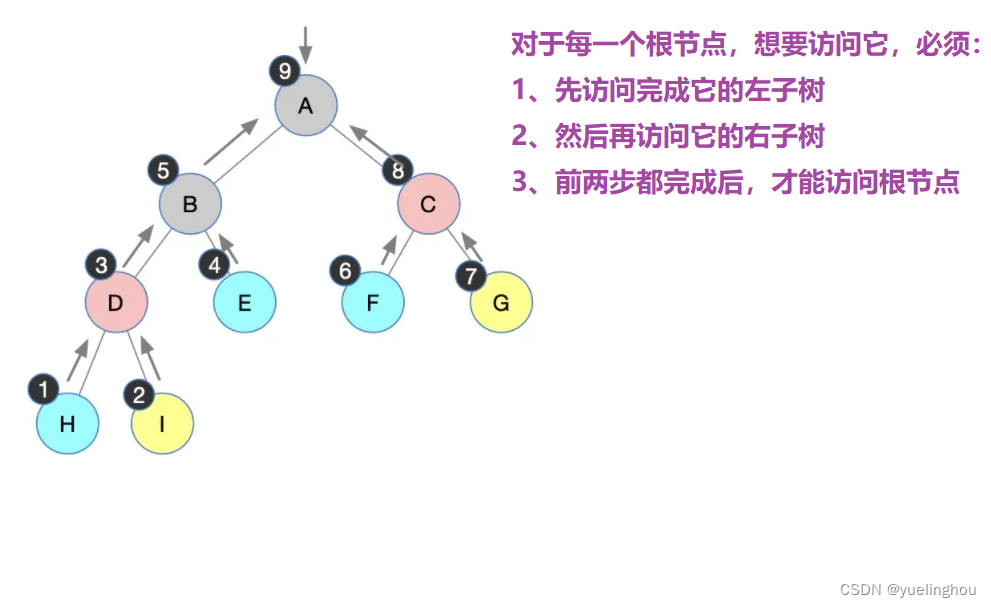
递归示例一：二叉树前序遍历

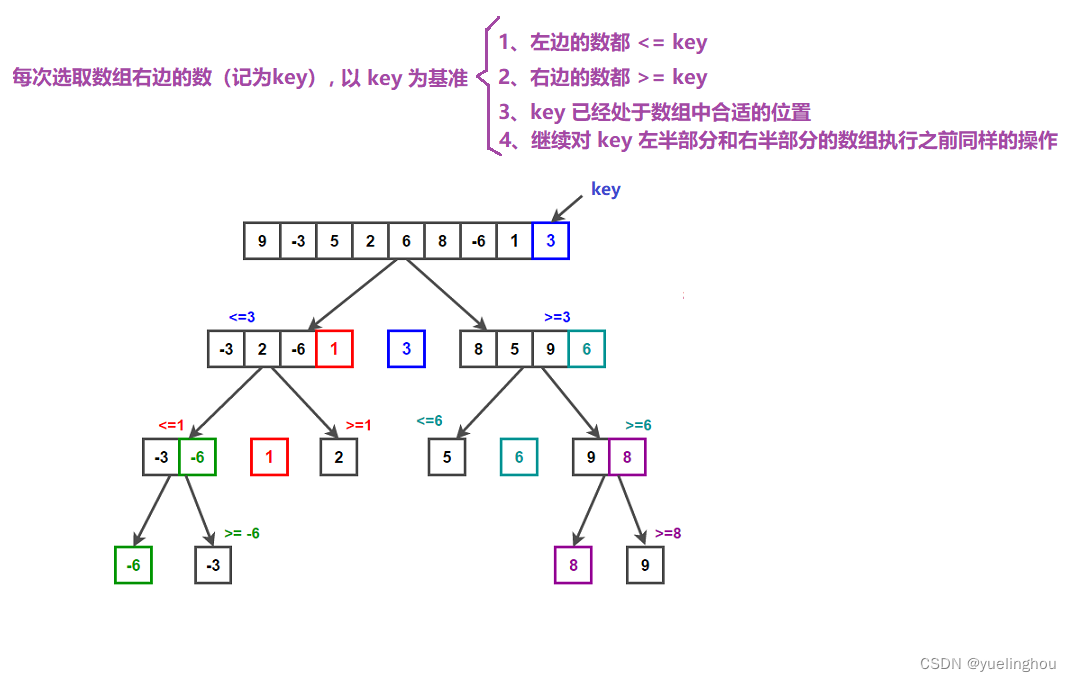
递归示例二：快速排序

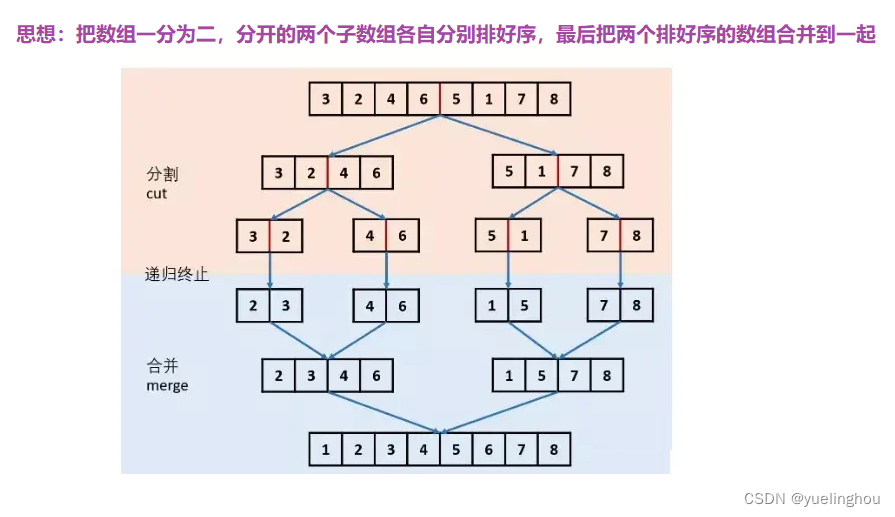
递归示例三：归并排序

1.3 如何理解递归？

实际处理递归问题时，如果能够宏观地看待递归，那么代码就会特别好写。其实做多了一些二叉树类的递归题目后，我们大抵就能够宏观地看待和理解递归了，可以总结出以下三个方面：

• 不要在意递归的细节展开图，这会让你做题目时非常痛苦
• 把递归的函数当成一个黑盒，我们只用传入参数，然后等待它返回给我们结果
• 相信这个黑盒一定能完成任务

举例：二叉树的后序遍历

1.4 如何写好一个递归？

1. 先找到相同的子问题（可以帮助我们完成函数头的设计）
2. 只关心某一个子问题是如何解决的（有助于我们完成函数体的书写）
3. 注意一下递归函数的出口（考虑哪些情况下，递归不能再进行下去）

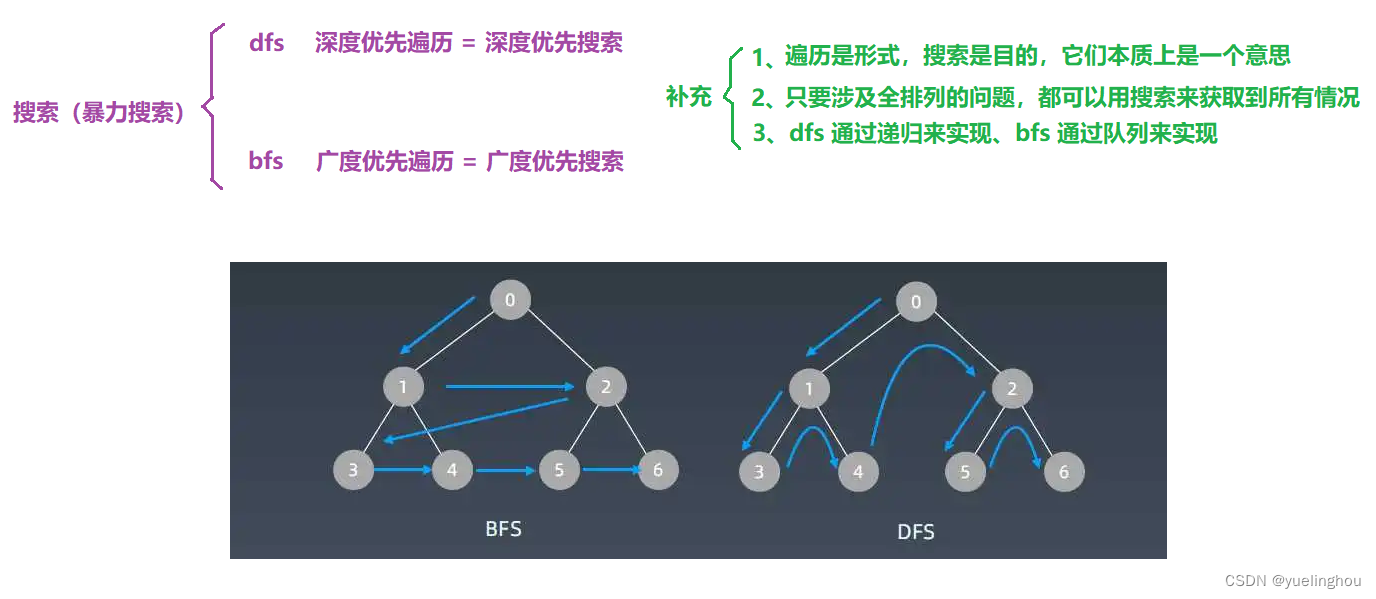
2. 遍历和搜索

3. 回溯和剪枝

下面我们通过一个走迷宫的例子来解释回溯和剪枝：

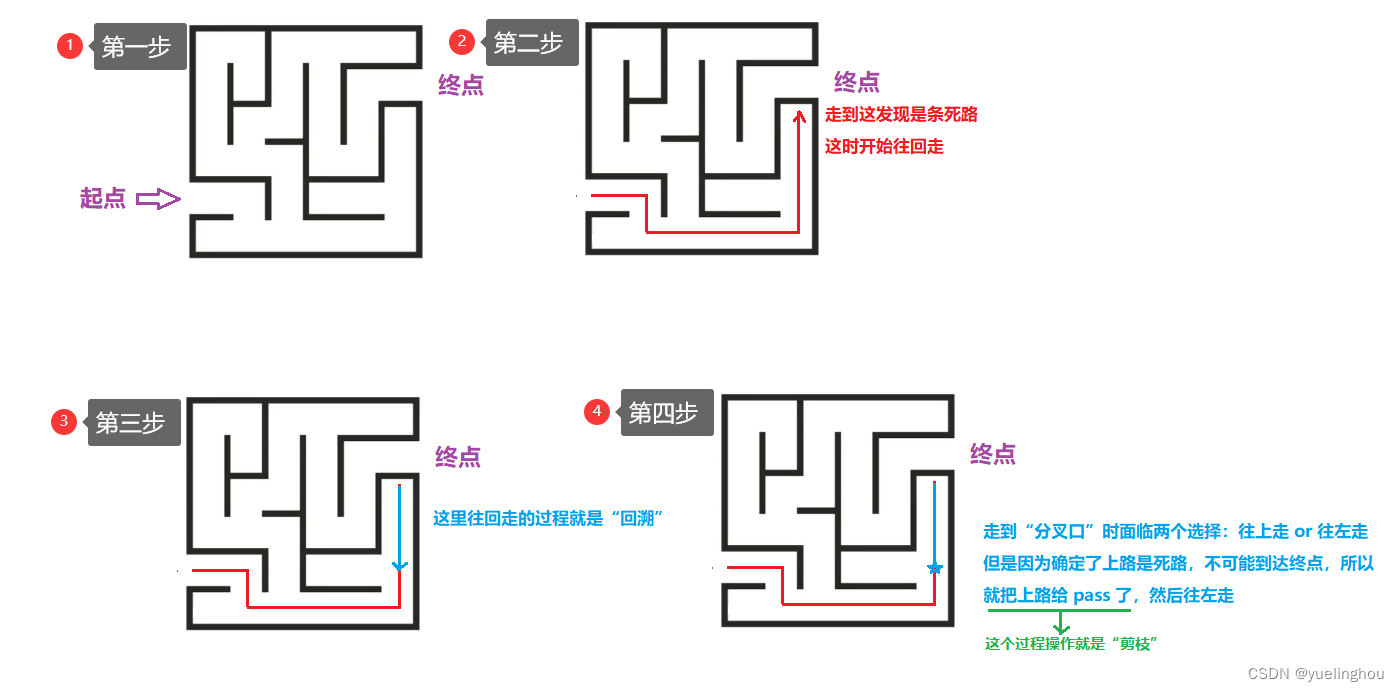
我们在看题解的时候，经常看到有些人用深搜，有些人用广搜，还有些人用回溯；其实回溯就是深度优先搜索。

二. 递归系列专题

---

1. 汉诺塔问题

---

题目链接

算法原理

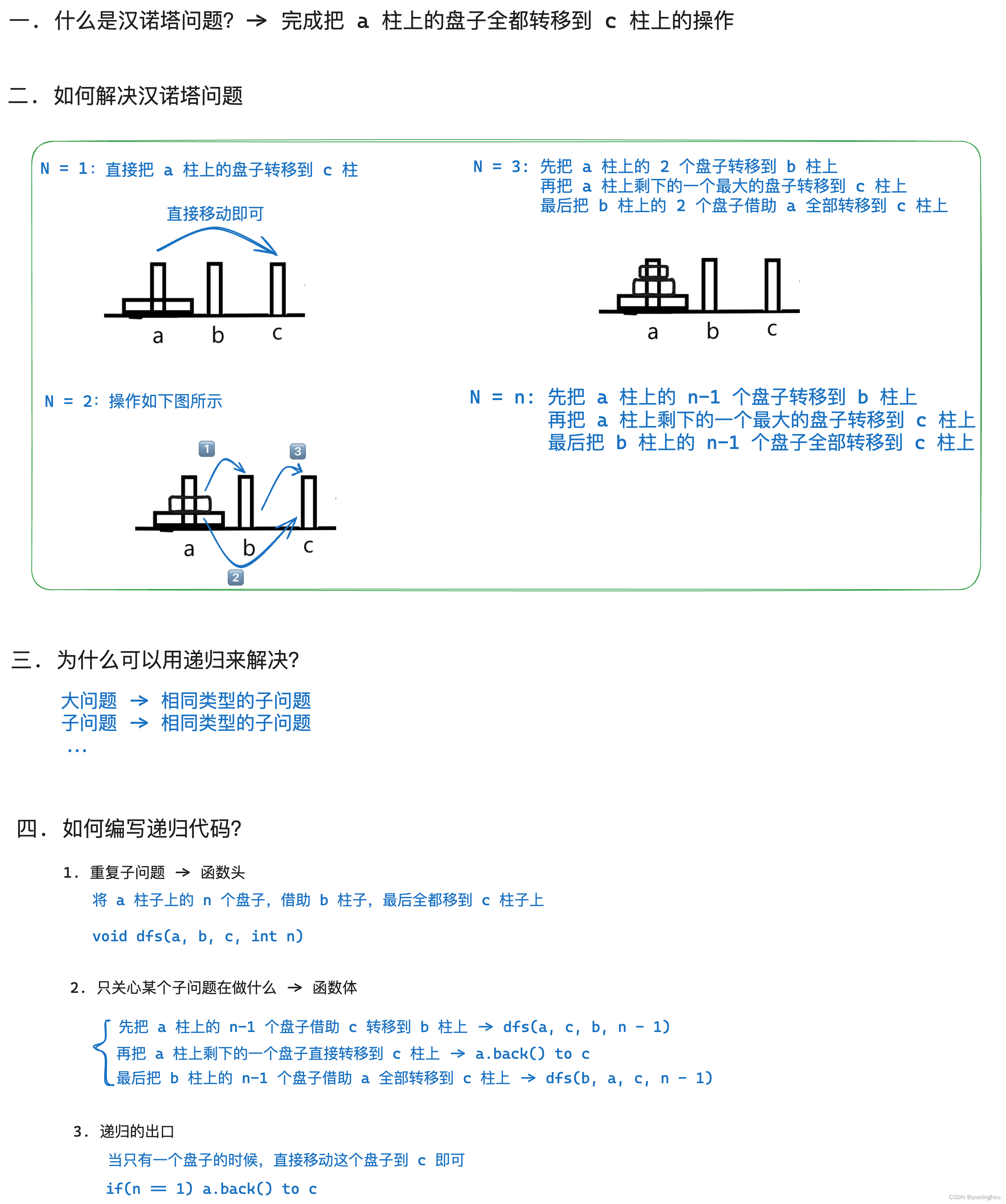
代码编写

class Solution 
{
private:
    void dfs(vector<int>& A, vector<int>& B, vector<int>& C, int n) 
    {
        // 0、递归出口：只剩一个盘子的话就直接移动
        if(n == 1) 
        {
            C.push_back(A.back());
            A.pop_back();
            return;
        }
        // 1. 先把 a 柱上 n - 1 个盘子借助 c 移动到 b 柱
        dfs(A, C, B, n - 1);
        // 2. 再把 a 柱剩下的一个盘子直接移动到 c 柱
        C.push_back(A.back());
        A.pop_back();
        // 3. 最后再把 b 柱上的 n - 1 个盘子借助 a 移动到 c 柱
        dfs(B, A, C, n - 1);
    }

public:
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) 
    {
        dfs(A, B, C, A.size());
    }
};

---

2. 合并两个有序链表

---

题目链接

算法原理

代码编写

class Solution 
{
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) 
    {
        // 0、特殊情况处理
        if(!list1) return list2;
        if(!list2) return list1;
        // 1、比较第一个节点值的大小
        // 2、记录较小节点，继续合并后续链表
        // 3、返回合并后链表的头节点
        if(list1->val < list2->val) 
        {
            list1->next = mergeTwoLists(list1->next, list2);
            return list1;
        }
        else
        {
            list2->next = mergeTwoLists(list1, list2->next);
            return list2;
        }
    }
};

---

3. 反转链表

---

题目链接

算法原理

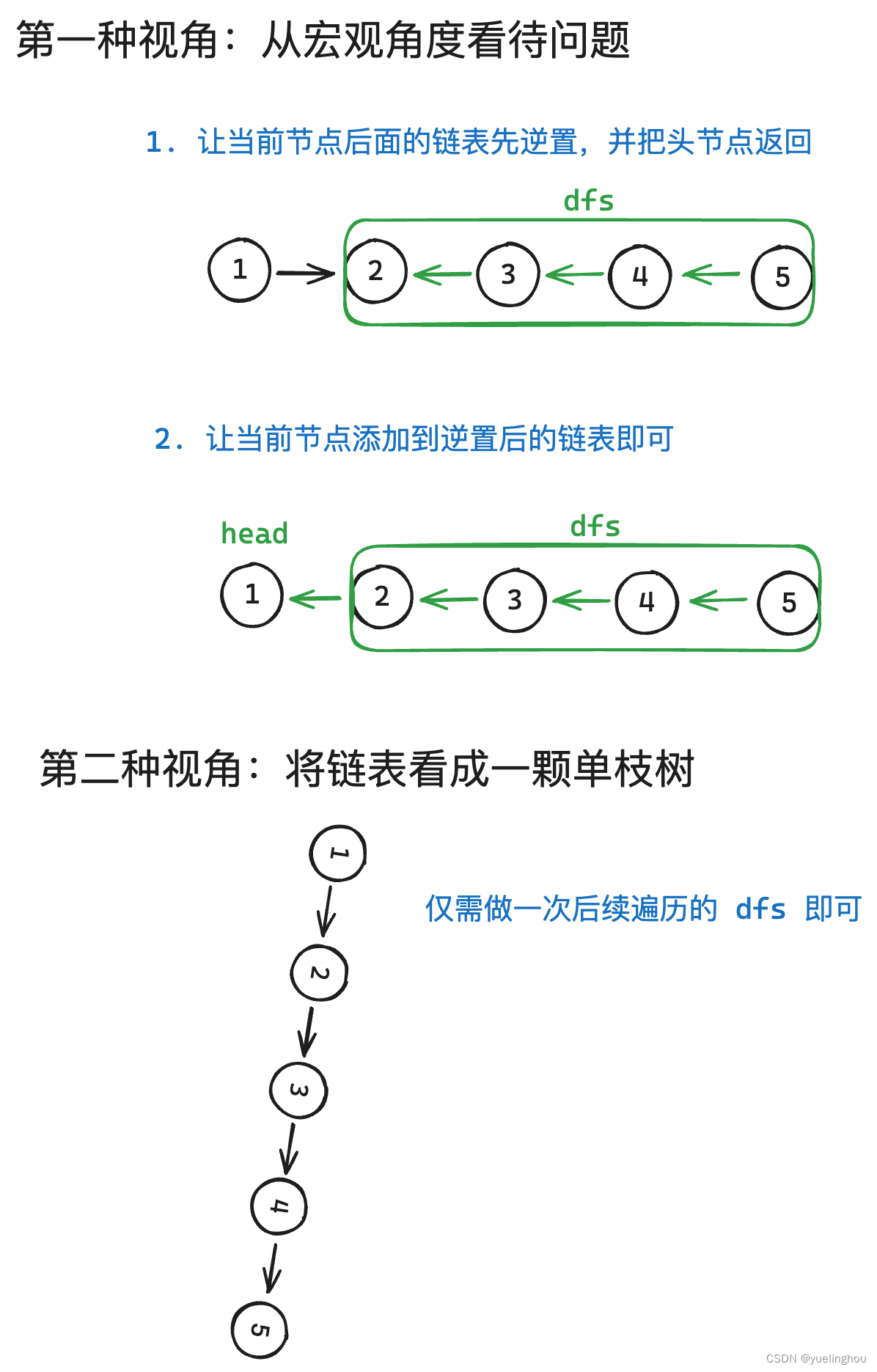
代码编写

class Solution 
{
public:
    ListNode* reverseList(ListNode* head) 
    {
        // 0、特殊情况处理
        if(!head || !head->next) return head;
        // 1、先逆置后面的链表
        ListNode* ans = reverseList(head->next);
        // 2、让当前节点添加到逆置后的链表
        head->next->next = head;
        head->next = nullptr;
        // 3、返回值
        return ans;
    }
};

---

4. 两两交换链表中的节点

---

题目链接

算法原理

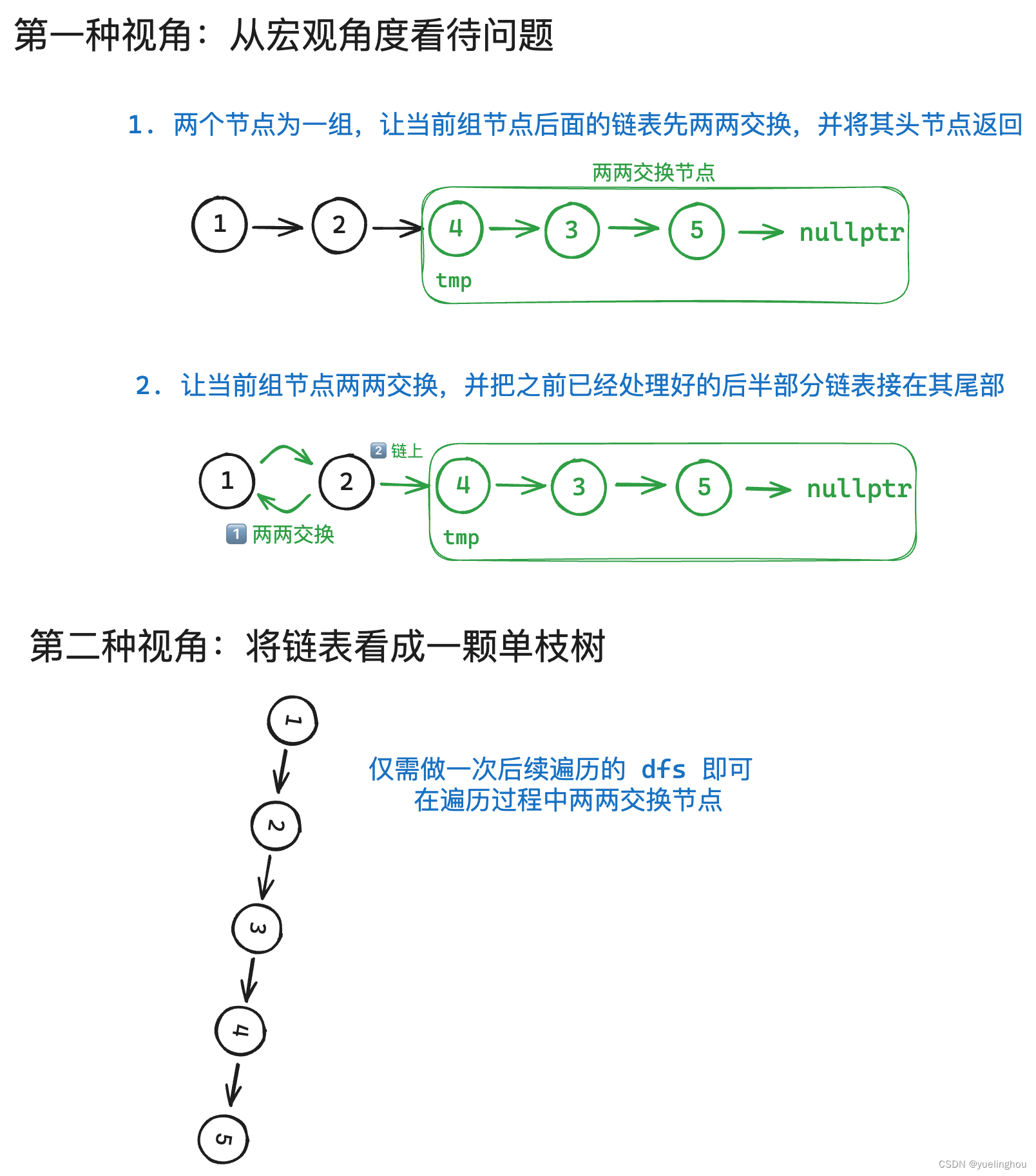
代码编写

class Solution 
{
public:
    ListNode* swapPairs(ListNode* head) 
    {
        // 0、特殊情况处理
        if(!head || !head->next) return head;
        // 1、先处理后部分链表两两交换
        auto tmp = swapPairs(head->next->next);
        // 2、对当前两个节点两两交换
        auto ans = head->next;
        head->next->next = head;
        head->next = tmp;
        // 3、返回值
        return ans;
    }
};

---

5. pow(x, n) - 快速幂

---

题目链接

算法原理

代码编写

class Solution 
{
private:
    double Pow(double x, long long n) 
    {
        if(!n) return 1;
        double tmp = Pow(x, n/2);
        return n % 2 == 1 ? tmp * tmp * x : tmp * tmp;
    }

public:
    double myPow(double x, int n) 
    {
        return n < 0 ? 1.0 / Pow(x, (long long)n * -1.0) : Pow(x, n);
    }
};