力扣785.判断二分图

存在一个?无向图?，图中有?n?个节点。其中每个节点都有一个介于?0?到?n - 1?之间的唯一编号。给你一个二维数组?graph?，其中?graph[u]?是一个节点数组，由节点?u?的邻接节点组成。形式上，对于?graph[u]?中的每个?v?，都存在一条位于节点?u?和节点?v?之间的无向边。该无向图同时具有以下属性：

• 不存在自环（graph[u]?不包含?u）。
• 不存在平行边（graph[u]?不包含重复值）。
• 如果?v?在?graph[u]?内，那么?u?也应该在?graph[v]?内（该图是无向图）
• 这个图可能不是连通图，也就是说两个节点?u?和?v?之间可能不存在一条连通彼此的路径。

二分图?定义：如果能将一个图的节点集合分割成两个独立的子集?A?和?B?，并使图中的每一条边的两个节点一个来自?A?集合，一个来自?B?集合，就将这个图称为?二分图?。

如果图是二分图，返回?true?；否则，返回?false?。

和本点有边相连的另一个点肯定是属于另一组的

我们先给一个起始点归到一组

与它直接相邻的点自然就归到另一组。

使用深度优先递归（也可以bfs）如果出现矛盾，即一个点被归到不同组，即错误。

本题可以省掉vis数组，是否遍历和归到哪组可以用一个数组标记

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        color=vector<int>(graph.size(),0);//color初值都是0，代表都未遍历
            for (int i = 0; i < graph.size(); ++i) {
                if (color[i] == 0) {
                    color[i]=1;//把i归到A组，之后开始深度优先遍历
                    bool ret=dfs(i,graph);
                    if(!ret) return false;
            }
        }
        return true;
    }
private:
    bool dfs(int src,vector<vector<int>>& graph){
        int nextColor=color[src]==1?2:1;//根据本点所属的组，决定相邻点的组号
        for(auto node:graph[src]){
            if(color[node]==0){//如果相邻点没被遍历过，就继续递归下去
                color[node]=nextColor;//相邻点归到另一组
                bool ret=dfs(node,graph);
                if(!ret) return false;
            }
            else if(color[node]!=nextColor)//如果相邻点之前遍历过，且被归到了和本点一样的组，即错误
                return false;
        }
        return true;
    }
    vector<int> color;//color数组用来标记是否遍历和归属的组，0是未遍历，1是A组，2是B组
};

力扣特别搞，原本以为从0开始就行，但它的测试点里有0是孤立点的情况，就错了😓

这个题的技巧是深度优先加染色，之前刚好也做到相似的题

力扣802.找到最终的安全状态

有一个有 n 个节点的有向图，节点按 0 到 n - 1 编号。图由一个 索引从 0 开始 的 2D 整数数组?graph表示，?graph[i]是与节点 i 相邻的节点的整数数组，这意味着从节点 i 到?graph[i]中的每个节点都有一条边。

如果一个节点没有连出的有向边，则该节点是 终端节点 。如果从该节点开始的所有可能路径都通向 终端节点 ，则该节点为 安全节点 。

返回一个由图中所有 安全节点 组成的数组作为答案。答案数组中的元素应当按 升序 排列。

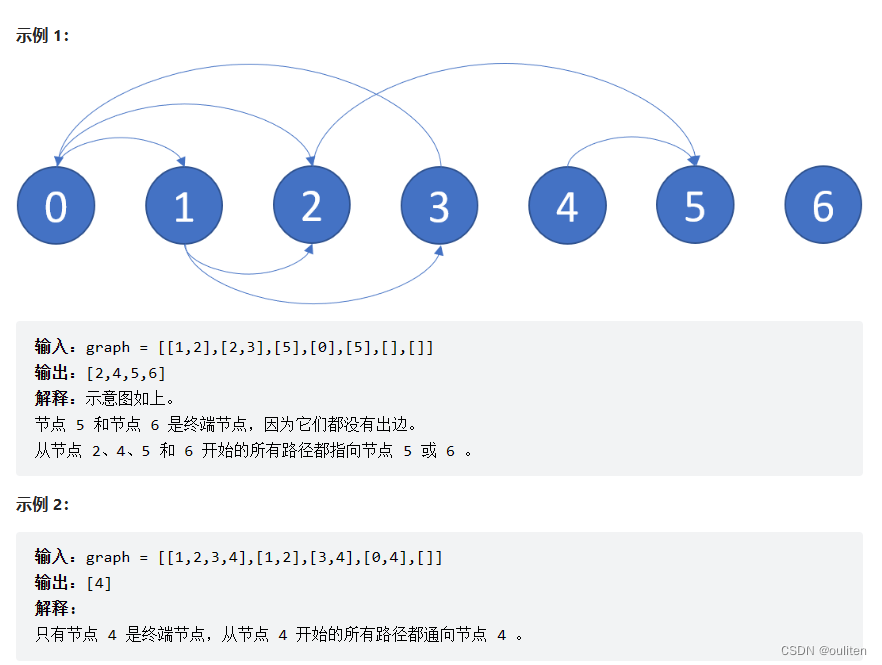
这个题的意思就是从一个点出发的路径不能遇到环。我们也可以使用染色的方法，第一次遇到的时候把该点染成1，表示走过一次，下次如果再遇到就表明走到环了，错误。

如果该点是安全节点，则标记为2，这样方便下次遇到直接利用。

可以先把终端节点标记成2。

class Solution {
public:
    vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
        color=vector<int>(graph.size(),0);
        vector<int> res;
        for(int i=0;i<graph.size();i++){
            if(graph[i].empty())//终端节点肯定是安全节点
                color[i]=2;
        }
        for(int i=0;i<graph.size();i++){
            bool ret=dfs(i,graph);
            if(ret) res.push_back(i);//安全就加入答案数组
        }
        return res;
    }
private:
    bool dfs(int src,vector<vector<int>>& graph){
        if(color[src]>0) return color[src]==2;//如果被遍历过，看是1还是2，1的话说明遇到环了，2表面安全
        color[src]=1;//遍历过1次，记录为1
        for(auto node:graph[src]){
            if(!dfs(node,graph))
                return false;
        }
        color[src]=2;//所有路径都正确，标记为安全节点
        return true;
    }
    vector<int> color;//0未遍历，1遍历过一次，2安全节点
};