算法训练第五十三天|1143. 最长公共子序列、1035. 不相交的线、53. 最大子数组和
1143. 最长公共子序列:
题目链接
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 :
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
解答:
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int[][] dp = new int[text1.length()+1][text2.length()+1];
for (int i = 1; i <text1.length() + 1; i++) {
for (int j = 1; j <text2.length() + 1; j++) {
if(text1.charAt(i-1)==text2.charAt(j-1)){
dp[i][j] = dp[i-1][j-1] + 1;
}else{
dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[text1.length()][text2.length()];
}
}
算法总结:
本题类似于昨天做的最长重复子数组,但不一样的是那题要求是连续的,本题并没有对连续做限制,则意味着在递推公式处理时并不一样,相同时处理逻辑是一样的,但在不相同时我们可以对dp进行dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);处理,即将两个子串前一个更大的赋值给dp
1035. 不相交的线:
题目链接
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
nums1[i] == nums2[j]
且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 :
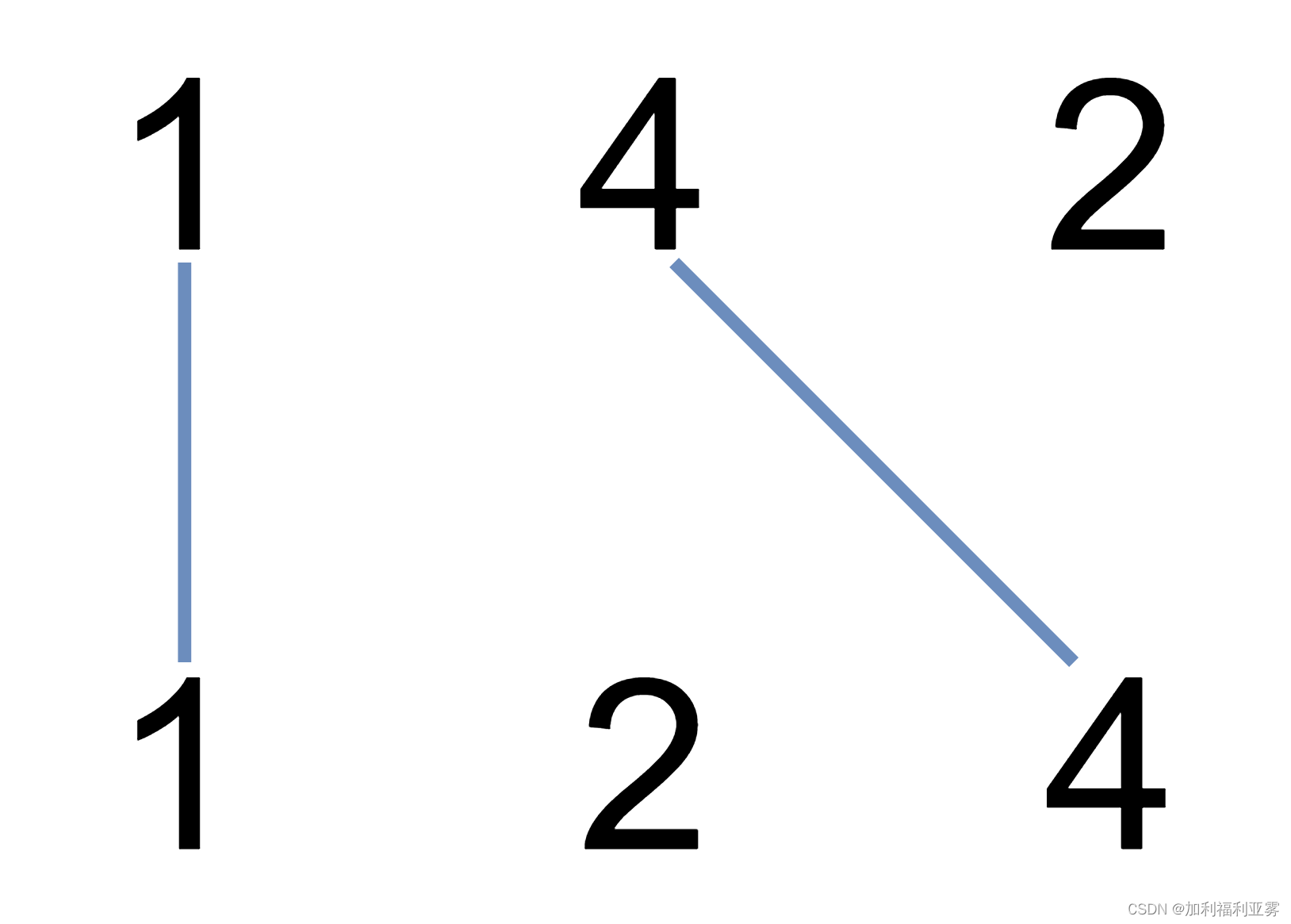
输入:nums1 = [1,4,2], nums2 = [1,2,4]
输出:2
解释:可以画出两条不交叉的线,如上图所示。
但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。
解答:
class Solution {
public int maxUncrossedLines(int[] nums1, int[] nums2) {
int[][] dp = new int[nums1.length+1][nums2.length+1];
for (int i = 1; i <=nums1.length ; i++) {
for (int j = 1; j <=nums2.length ; j++) {
if(nums1[i-1]==nums2[j-1]){
dp[i][j] = dp[i-1][j-1] + 1;
}else{
dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[nums1.length][nums2.length];
}
}
算法总结:
本题我们可以根据题意分析出来,本质上实际上就是一个最长公共子序列的变式,通过同样的套路求解即可。
53. 最大子数组和:
题目链接
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 :
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
解答:
class Solution {
public int maxSubArray(int[] nums) {
if(nums.length==1)return nums[0];
int[] dp = new int[nums.length+1];
int max = nums[0];
for (int i = 1; i <=nums.length ; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i-1], nums[i-1]);
max = Math.max(max,dp[i]);
}
return max;
}
}
算法总结:
最大子数组和这题问题难点在于如何精确寻找每一个子数组的起始位置,通过分析我们实际上不难发现,我们只要比较当前求和的值和nums本身的值即可。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!