时间序列预测模型介绍及使用经验总结

时间序列预测模型，常用的机器学习模型主要包括以下3类：ARIMA，Prophet，LGB。这3类模型的优缺点如下：

（1）ARIMA

①优点

• 简单易行，可解释性强；

• 数据量要求低；

• 计算速度较快，可以对每个站在线拟合推理；

②缺点

• 仅支持单变量；

• 无法特征工程；

• 准确率低；

③适用场景：基于统计学方法，项目初期冷启动

（2）Prophet

①优点

• 简单易行，可解释性强；

• 数据量要求低；

• 加入先验知识（节假日）；

• 计算速度更快，可以对每个站在线拟合推理；

②缺点

• 仅支持单变量；

• 无法特征工程；

• 准确率较低；

③适用场景：项目初期迭代

（3）LGB

①优点

• 准确率较高；

• 简单易行，可解释性强；

• 支持批量预测，计算速度更快；

②缺点

• 迭代模型等于迭代特征，但是迭代特征存在瓶颈；

• 对类别特征利用不充分；

③适用场景：项目中期迭代

3.深度学习模型

前文提到，机器学习的可操作性以及模型效果都是有限的，会遇到瓶颈，因此引入深度学习模型：

①?深度学习模型架构

时序预测任务所涉及到的CNNs、RNNs和Transformers等模型都属于生成模型，具有统一的架构（unified architecture），这样的架构有两个重点部分，一个是Embedding引擎部分，另一个是编码器-解码器部分，如下图所示：

• TCN模型的编码器和解码器主要是1D卷积网络；

• CRNN模型的编码器和解码器主要是1D卷积网络和RNN网络；

• Informer模型的编码器和解码器主要是Transformer网络；

• DCN模型的编码器和解码器主要是2D卷积网络；

2. 时序预测痛点：

一个是节假日时间不固定问题，另一个是时间先验问题。

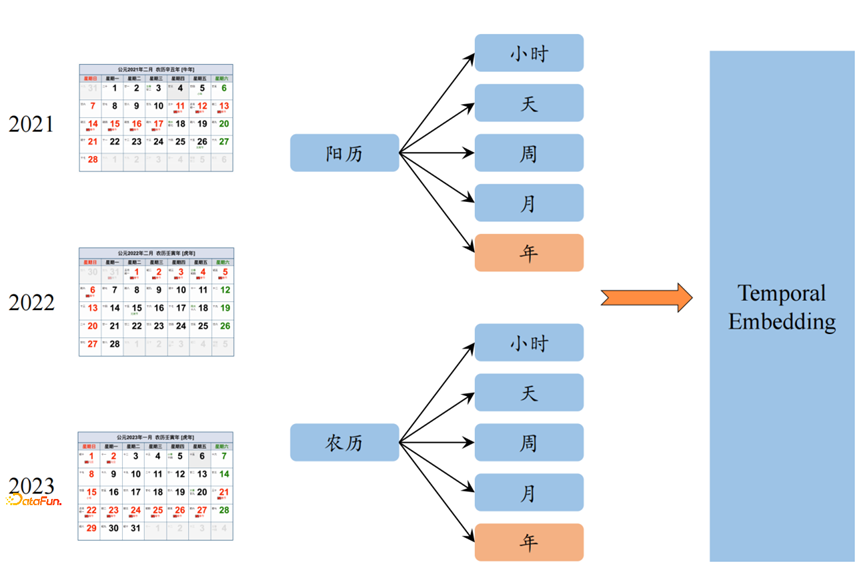
• Temporal Embedding。Temporal Embedding主要用来解决两个问题，一个是节假日时间不固定问题，另一个是时间先验问题。

1. 对于第一个节假日不固定问题，我们的节假日包括阳历节日和农历节日；根据序列的时间周期可以拆分成小时、天、周、月、年等常规周期；

对于节假日时间的对齐方式，包括硬对齐和软对齐两种方式。

1. 硬对齐主要指序列按照周、月、年等方式进行序列对齐，
2. 软对齐主要是指将序列进行傅里叶变换（时序->频域），找到序列的 主频，借助序列的频域信息进行对齐。

2. 对于第二个时间先验问题，如下图所示，预测的时间数据已知，但是?其它相关输入变量 未知，这就造成了输入数据的维度不一致；

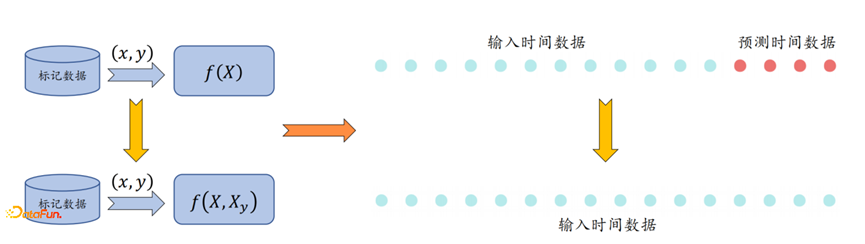
对于上述问题，通过填充?未知的其他变量?保证?输入数据的 维度一致，并根据位置的标记?区分 已知变量和未知变量，最终可以得到输出的预测变量。

2. 卷积模块设计经验

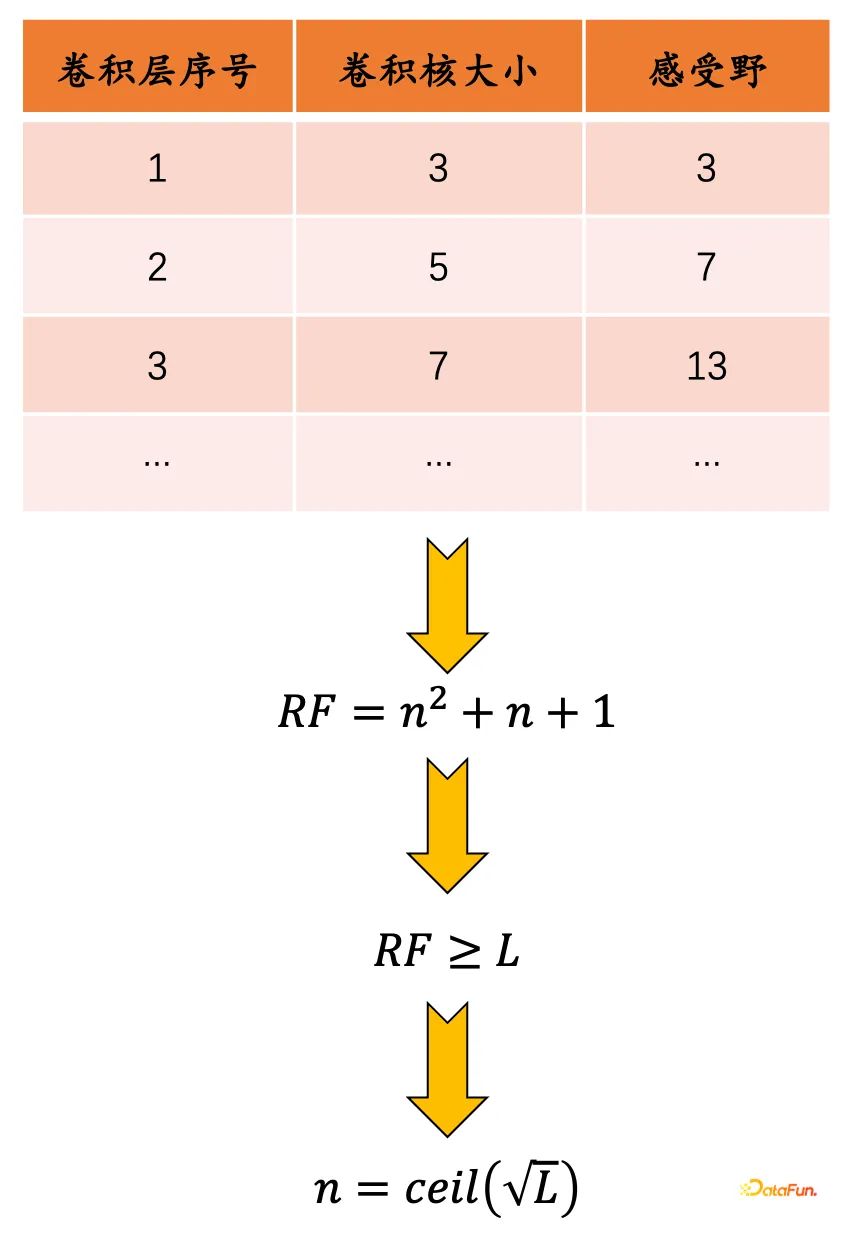
DCN部分中卷积层的设计，首先面临如下的思考：假设输入序列长度等于L，第i个卷积层的卷积核大小等于2i+1，步长等于1，需要多少卷积层？

这里涉及到两个概念：

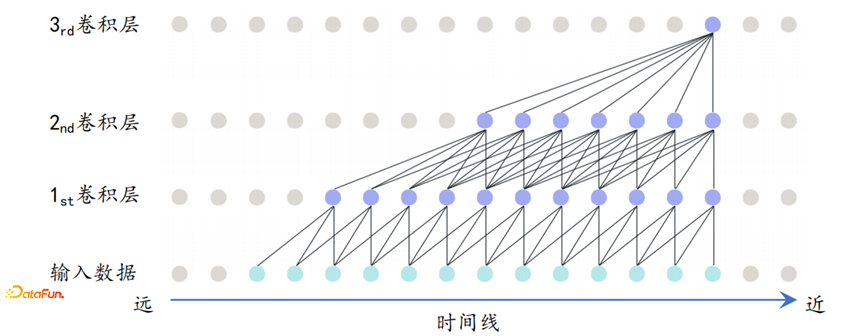
• 因果卷积

• 时间序列本身存在因果关系，即在某一时间点t，只能获取历史信息，而无法获取未来信息；

• 使用下图所示的单边卷积，用来保证序列的时间因果关系。

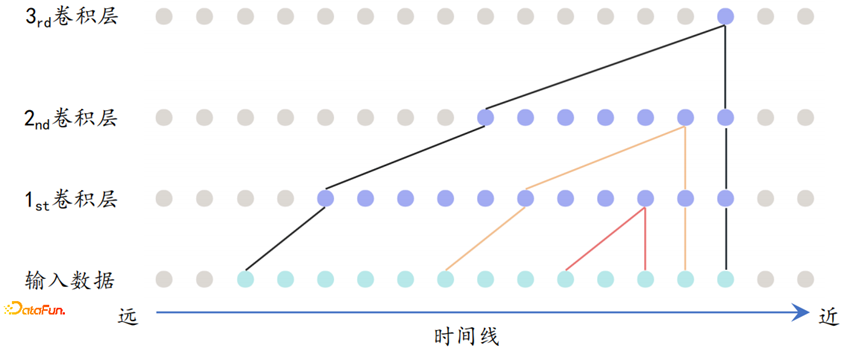
• 感受野

• 感受野主要是指将一个特征点映射回到原始输入，所覆盖的范围；

• 需要保证卷积神经网络可以覆盖到 输入时间序列的长度范围；

• 感受野可以通过下图的表格计算，得到的n就是需要设置的卷积层数

  • 第i个卷积层的卷积核大学： 2i+1

  • 感受野： i^2+i+1

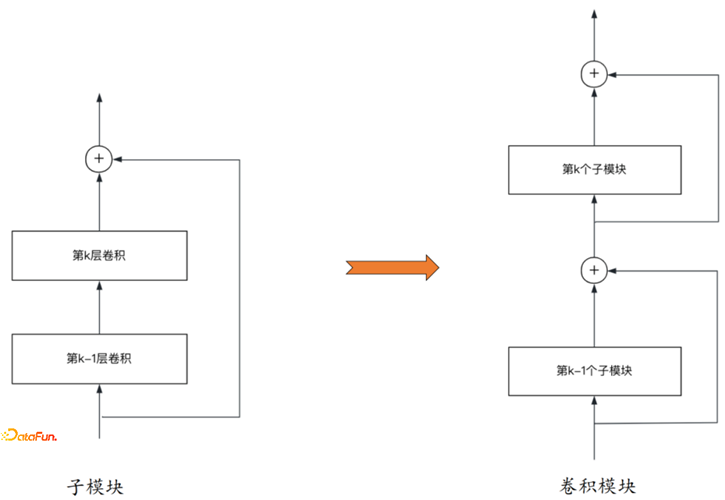
确定了卷积层的层数，将卷积层通过残差层子模块，像搭积木一样连接成整体的网络模块。

4.模型融合

模型融合方面，有三个问题值得思考：

• 加法还是减法？

  • 减法 主要包括残差、GBDT、Shortcut等；

  • 加法 主要包括stacking等方法；

• 分类还是回归？

  • 传统的预测一般是回归问题；

  • 类问题往往会涉及概率问题，通过投票选择可以获得一定的信息；

• 向上、向下还是躺平？

  • 使用基模型进行预测，可通过强化学习对预测效果进行反馈与激励，引导模型自主学习。

?