朴素贝叶斯 朴素贝叶斯原理

朴素贝叶斯 朴素贝叶斯原理

判别模型和生成模型

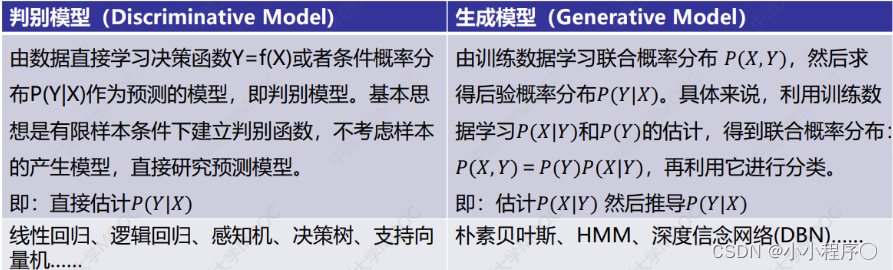
• 监督学习方法又分生成方法 (Generative approach) 和判别方法 (Discriminative approach)所学到的模型分别称为生成模型 (Generative Model) 和判别模型 (Discriminative Model)。

朴素贝叶斯原理

1. 朴素贝叶斯法是典型的生成学习方法。生成方法由训练数据学习联合概率分布$P(X,Y)$，然后求得后验概率分布$P(Y|X)$。具体来说，利用训练数据学习$P(X|Y)$和$P(Y)$的估计，得到联合概率分布：

   $$P(X,Y)＝P(Y)P(X|Y)$$

   概率估计方法可以是极大似然估计或贝叶斯估计。

2. 朴素贝叶斯法的基本假设是条件独立性

   $$\begin{array}{rl}P(X& =x|Y=c_k)=P\left(X^{(1)}=x^{(1)},?,X^{(n)}=x^{(n)}|Y=c_k\right)\\ & =\prod _{j=1}^{n}P\left(X^{(j)}=x^{(j)}|Y=c_k\right)\end{array}$$

   由于这一假设，朴素贝叶斯法的学习与预测大为简化。因而朴素贝叶斯法高效，且易于实现。其缺点是分类的性能不一定很高。

3. 朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测。

   $$P(Y|X)=\frac{P(X,Y)}{P(X)}=\frac{P(Y)P(X|Y)}{{\sum }_{Y}P(Y)P(X|Y)}$$ 将上述第2点的公式带入，由于各个概率的分母都是$$\sum _{Y}P(Y)P(X|Y)$$
   所以后验概率最大的类$y$为：
   $$y=\arg \underset{c_k}{\max }P\left(Y=c_k\right)\prod _{j=1}^{n}P\left(X_j=x^{(j)}Y=c_k\right)$$

   后验概率最大等价于0-1损失函数时的期望风险最小化。

GaussianNB 高斯朴素贝叶斯

特征的可能性被假设为高斯

概率密度函数：
$$P(x_i|y_k)=\frac{1}{\sqrt{2\pi {\sigma }_{yk}^2}}exp(?\frac{(x_i?{\mu }_{yk}{)}^2}{2{\sigma }_{yk}^2})$$

数学期望(mean)：$\mu$

方差：${\sigma }^2=\frac{\sum (X?\mu {)}^2}{N}$