Openjudge 7834:分成互质组题解
2023-12-31 03:51:41
前言:
查了几个小时,真的查裂开了,所以我必须吐槽一下
原题目:OpenJudge - 7834:分成互质组
问题描述:
给定n个正整数,将它们分组,使得每组中任意两个数互质。至少要分成多少个组?
输入格式
第一行是一个正整数n。1 <= n <= 10。
第二行是n个不大于10000的正整数。
输出格式
一个正整数,即最少需要的组数。
样例输入
6
14 20 33 117 143 175
样例输出
3
问题解释
几组问题的解(如下)
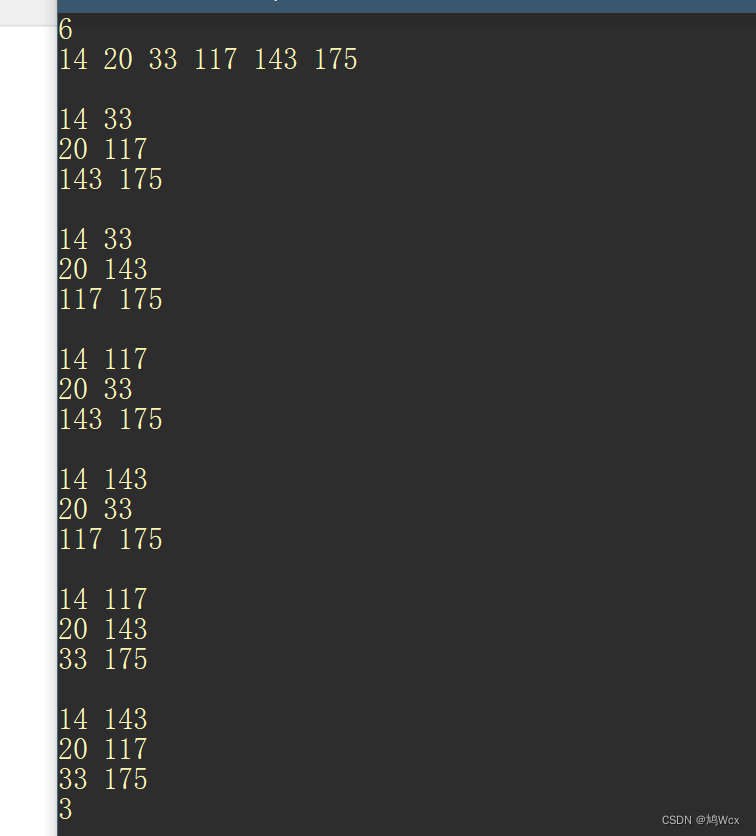
由于数据不太大,所以我们可以用搜索的方式解决,先将数字分组,再进行判断,保留最优值ans(组数)
搜索
在这里,我运用了动态数组vector,它可以自动开辟数组大小
vetcor<int> v[15] 表示:15个组的动态数组v[]
核心代码如下:
v[1].push_back(a[1]);
开辟第一组,所以a[1]只能放入第一组
dfs(2,1);
搜索第二个数,当前组数为1void dfs(int t,int num) 搜索第t个数字的情况,目前开辟的组数
{
if (num>ans) return ;
剪枝,如果组数已经大于最优值ans,就没有再搜的必要了
if (t==n+1)
{
已经将n个数都分好了组,接下来进行判断
if (pd(num)) ans=min(ans,num);
如果符合条件,则将ans更新为当前的组数
return ;
结束,返回上一层(必须写)
}
for (int j=1;j<=num+1;j++)
{
v[j].push_back(a[t]);
将a[t]放入第j组
dfs(t+1,max(num,j));
下一层搜索,如果j=num+1>num,表示为a[t]单独开辟一组
v[j].pop_back();
回溯,将a[t]从j组拿出,重新放进别的组
}
}判断当前分的数是否满足条件:?
bool pd(int m)
{
判断当前分组是否满足条件
for (int i=1;i<=m;i++)
{
查看第i组
int len=v[i].size();
len记录当前i组有多少个数
for (int j=0;j<len;j++)
{
注意:动态数组将数放入组时,从0号开始放
for (int k=j+1;k<len;k++)
{
判断两两间是否互质(最大公约数gcd==1)
if (gcd(v[i][j],v[i][k])!=1) return false;
不满足,返回false(假)
}
}
}
return true;
满足条件,返回true(真)
}求两数的最大公约数:
int gcd(int x,int y)
{
int r=x%y;
while (r)
{
x=y;
y=r;
r=x%y;
}
return y;
辗转相除法
}图形化证明:
在看了许多证明,我认为都没有解释的很清楚,所以我选择用我的方法证明一下

根据上面的代码,我们将其带入,要求的最大公约数x,就是能用x*x的小正方形围成a*b的最大正方形,用当前的短边b*b填充a*b,留下的面积是长边为b,所以在剩下的面积中找出的正方形,一定能围成b*b的正方形,依次类推,求出恰好能填充剩余面积的小正方形,它的边长就是a和b的最大公约数
Ac代码如下:
#include <bits/stdc++.h>
using namespace std;
int n,r,ans=25;
vector<int> v[15];
int a[25];
int gcd(int x,int y)
{
int r=x%y;
while (r)
{
x=y;
y=r;
r=x%y;
}
return y;
}
bool pd(int m)
{
for (int i=1;i<=m;i++)
{
int len=v[i].size();
for (int j=0;j<len;j++)
{
for (int k=j+1;k<len;k++)
{
if (gcd(v[i][j],v[i][k])!=1) return false;
}
}
}
return true;
}
void dfs(int t,int num)
{
if (num>ans) return ;
if (t==n+1)
{
if (pd(num)) ans=min(ans,num);
return ;
}
for (int j=1;j<=num+1;j++)
{
v[j].push_back(a[t]);
dfs(t+1,max(num,j));
v[j].pop_back();
}
}
int main ()
{
int i,j;
cin>>n;
for (i=1;i<=n;i++)
{
cin>>a[i];
}
v[1].push_back(a[1]);
dfs(2,1);
cout<<ans;
return 0;
}
成功Ac,完结撒花~!
如有不解或优化,可在评论区留言
文章来源:https://blog.csdn.net/inhuibin/article/details/135309899
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!