【python学习】-用matplotlib实现将二维数据绘制为三维图形（三维多线图）并实战(三维散点图)

绘制一幅三维线图

#将二维数据绘制三维图（三维多线图）
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
import numpy as np
x=np.linspace(0,20,40)
y=2
y=y*np.ones(40)#保证与x轴的点数一致，这一步非常重要
z=np.sin(x * 2 * np.pi) / 2 + 0.5

ax = plt.figure().add_subplot(projection='3d')
ax.plot(x,y,z)#绘图

# 图像的其他参数设置
ax.view_init(15, -20)#图形展示角度
#ax.grid(False)#去掉网格
ax.w_xaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))#背景设置为白色
ax.w_yaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
ax.w_zaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
#坐标及坐标轴相关设置
ax.set_xlabel('x') #x轴坐标名称及字体样式
ax.set_ylabel('y') #x轴坐标名称及字体样式
ax.set_zlabel('z') #z轴坐标名称及字体样式
#ax.set_xlim(0,20)#x轴范围
#ax.set_zlim(0,40)
ax.set_yticks([1,2,3,4,5]) #y轴刻度字体大小
plt.show()

结合for循环绘制多幅三维线图（在一幅图上）

#将二维数据绘制三维图（三维多线图）
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
import numpy as np
x=np.linspace(0,20,40)
y_list=[1,3,5]

z=np.sin(x * 2 * np.pi) / 2 + 0.5

ax = plt.figure().add_subplot(projection='3d')
#结合for循环绘制多张线图
for i in range(0,3,1):
    y=y_list[i]
    y=y*np.ones(40)#保证与x轴的点数一致，这一步非常重要
    ax.plot(x,y,z)#绘图

# 图像的其他参数设置
ax.view_init(15, -20)#图形展示角度
#ax.grid(False)#去掉网格
ax.w_xaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))#背景设置为白色
ax.w_yaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
ax.w_zaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
#坐标及坐标轴相关设置
ax.set_xlabel('x') #x轴坐标名称及字体样式
ax.set_ylabel('y') #x轴坐标名称及字体样式
ax.set_zlabel('z') #z轴坐标名称及字体样式
#ax.set_xlim(0,20)#x轴范围
#ax.set_zlim(0,40)
ax.set_yticks([1,2,3,4,5]) #y轴刻度字体大小
plt.show()

美化图形

主要是调整图形清晰度，坐标轴以及图形颜色，线的粗细，添加label

#美化图形
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
import numpy as np
x=np.linspace(0,20,40)
y_list=[1,3,5]
z=np.sin(x * 2 * np.pi) / 2 + 0.5
color_list=['red','tab:blue','tab:green']#颜色
font3 = {'family' : 'Arial',
    'weight' : 'normal',
    'size'   : 14,
    }
ax = plt.figure().add_subplot(projection='3d')
#结合for循环绘制多张线图
for i in range(0,3,1):
    y=y_list[i]
    y=y*np.ones(40)#保证与x轴的点数一致，这一步非常重要
    ax.plot(x,y,z,linewidth=1,label='y='+str(y_list[i]),color=color_list[i])#绘图

# 图像的其他参数设置
ax.view_init(15, -20)#图形展示角度
ax.grid(False)#去掉网格
ax.w_xaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))#背景设置为白色
ax.w_yaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
ax.w_zaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
#坐标及坐标轴相关设置
ax.legend(frameon=False,fontsize='small',loc='center left') #设置图例及图中文本显示
ax.set_xlabel('x',font3) #x轴坐标名称及字体样式
ax.set_ylabel('y',font3) #x轴坐标名称及字体样式
ax.set_zlabel('z',font3) #z轴坐标名称及字体样式
ax.set_xlim(0,20)#x轴范围
#ax.set_zlim(0,40)
ax.set_yticks([1,2,3,4,5]) #y轴刻度字体大小

plt.rcParams['figure.figsize']=(8.0,6.0)
plt.rcParams['savefig.dpi'] = 200 #图片像素
plt.rcParams['figure.dpi'] = 200 #分辨率
plt.show()

截至此，内容来源于 [https://blog.csdn.net/qq_40481843/article/details/120888436](https://blog.csdn.net/qq_40481843/article/details/120888436) # 实战 这里需要自己找一张图片并修改为lena.png，放在py文件同级目录下

import cv2
import numpy as np
import matplotlib.pyplot as plt


'''
分别计算图像通道相邻像素的水平、垂直和对角线的相关系数并返回
'''
def RGB_correlation(channel,N):
  #计算channel通道
  h,w=channel.shape
  #随机产生pixels个[0,w-1)范围内的整数序列
  row=np.random.randint(0,h-1,N)
  col=np.random.randint(0,w-1,N)
  #绘制相邻像素相关性图,统计x,y坐标
  x=[]
  h_y=[]
  v_y=[]
  d_y=[]
  for i in range(N):
    #选择当前一个像素
    x.append(channel[row[i]][col[i]])
    #水平相邻像素是它的右侧也就是同行下一列的像素
    h_y.append(channel[row[i]][col[i]+1])
    #垂直相邻像素是它的下方也就是同列下一行的像素
    v_y.append(channel[row[i]+1][col[i]])
    #对角线相邻像素是它的右下即下一行下一列的那个像素
    d_y.append(channel[row[i]+1][col[i]+1])
  #三个方向的合到一起
  x=x*3
  y=h_y+v_y+d_y

  #结果展示
  # plt.rcParams['font.sans-serif'] = ['SimHei']  # 中文乱码
  # plt.scatter(x,y)
  # plt.show()

  #计算E(x)，计算三个方向相关性时，x没有重新选择也可以更改
  ex=0
  for i in range(N):
    ex+=channel[row[i]][col[i]]
  ex=ex/N
  #计算D(x)
  dx=0
  for i in range(N):
    dx+=(channel[row[i]][col[i]]-ex)**2
  dx/=N

  #水平相邻像素h_y
  #计算E(y)
  h_ey=0
  for i in range(N):
    h_ey+=channel[row[i]][col[i]+1]
  h_ey/=N
  #计算D(y)
  h_dy=0
  for i in range(N):
    h_dy+=(channel[row[i]][col[i]+1]-h_ey)**2
  h_dy/=N
  #计算协方差
  h_cov=0
  for i in range(N):
    h_cov+=(channel[row[i]][col[i]]-ex)*(channel[row[i]][col[i]+1]-h_ey)
  h_cov/=N
  h_Rxy=h_cov/(np.sqrt(dx)*np.sqrt(h_dy))

  #垂直相邻像素v_y
  #计算E(y)
  v_ey=0
  for i in range(N):
    v_ey+=channel[row[i]+1][col[i]]
  v_ey/=N
  #计算D(y)
  v_dy=0
  for i in range(N):
    v_dy+=(channel[row[i]+1][col[i]]-v_ey)**2
  v_dy/=N
  #计算协方差
  v_cov=0
  for i in range(N):
    v_cov+=(channel[row[i]][col[i]]-ex)*(channel[row[i]+1][col[i]]-v_ey)
  v_cov/=N
  v_Rxy=v_cov/(np.sqrt(dx)*np.sqrt(v_dy))

  #对角线相邻像素d_y
  #计算E(y)
  d_ey=0
  for i in range(N):
    d_ey+=channel[row[i]+1][col[i]+1]
  d_ey/=N
  #计算D(y)
  d_dy=0
  for i in range(N):
    d_dy+=(channel[row[i]+1][col[i]+1]-d_ey)**2
  d_dy/=N
  #计算协方差
  d_cov=0
  for i in range(N):
    d_cov+=(channel[row[i]][col[i]]-ex)*(channel[row[i]+1][col[i]+1]-d_ey)
  d_cov/=N
  d_Rxy=d_cov/(np.sqrt(dx)*np.sqrt(d_dy))

  return h_Rxy,v_Rxy,d_Rxy,x,y

'''
分别计算图像img的各通道相邻像素的相关系数，默认随机选取3000对相邻像素
'''
def correlation(img,N=3000):
  img=cv2.imread(img)
  h,w,_=img.shape
  B,G,R=cv2.split(img)
  R_Rxy=RGB_correlation(R,N)
  G_Rxy=RGB_correlation(G,N)
  B_Rxy=RGB_correlation(B,N)

  x_list = [1,3,5]
  y_list = [R_Rxy[3], G_Rxy[3], B_Rxy[3]]
  z_list = [R_Rxy[4], G_Rxy[4], B_Rxy[4]]
  color_list = ['red', 'tab:blue', 'tab:green']  # 颜色
  font3 = {'family': 'Arial',
           'weight': 'normal',
           'size': 14,
           }
  ax = plt.figure().add_subplot(projection='3d')
  for i in range(0, 3, 1):
    x = x_list[i]
    x = x * np.ones(9000)
    y = y_list[i]
    z = z_list[i]
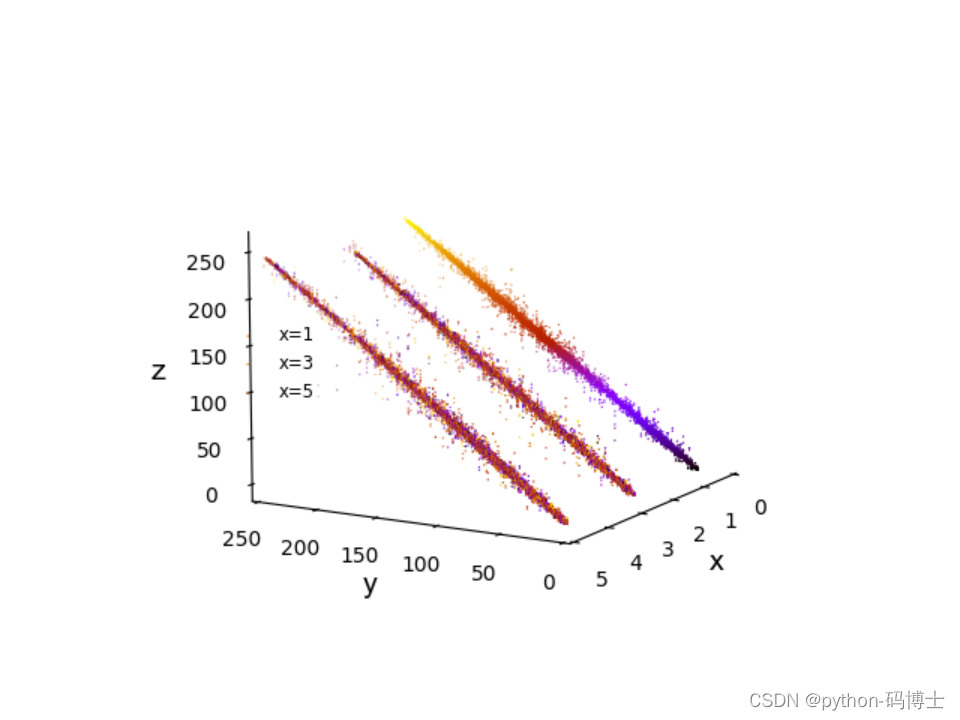
    ax.scatter(x, y, z, label='x=' + str(x_list[i]), c= R_Rxy[4], cmap=plt.cm.gnuplot, edgecolors='none',s=1)  # 绘图

  # 图像的其他参数设置
  ax.view_init(10, 30)  # 图形展示角度
  ax.grid(False)  # 去掉网格
  ax.xaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))  # 背景设置为白色
  ax.yaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
  ax.zaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
  # 坐标及坐标轴相关设置
  ax.legend(frameon=False, fontsize='small', loc='center left')  # 设置图例及图中文本显示
  ax.set_xlabel('x', font3)  # x轴坐标名称及字体样式
  ax.set_ylabel('y', font3)  # x轴坐标名称及字体样式
  ax.set_zlabel('z', font3)  # z轴坐标名称及字体样式
  ax.set_xlim(0, 5)  # x轴范围
  ax.set_ylim(250, 0)  # x轴范围
  # ax.set_zlim(0,40)
  # ax.set_xticks([1, 2, 3, 4, 5])  # y轴刻度字体大小

  plt.rcParams['figure.figsize'] = (8.0, 6.0)
  plt.rcParams['savefig.dpi'] = 200  # 图片像素
  plt.rcParams['figure.dpi'] = 200  # 分辨率
  plt.show()
#######################################
  # #结果展示
  # plt.rcParams['font.sans-serif'] = ['SimHei']  # 中文乱码
  # plt.subplot(221)
  # plt.imshow(img[:,:,(2,1,0)])
  # plt.title('原图像')
  # #子图2
  # plt.subplot(222)
  # # plt.scatter(R_Rxy[3],R_Rxy[4],s=1,c='red')
  # plt.scatter(R_Rxy[3],R_Rxy[4],c= R_Rxy[4], cmap=plt.cm.gnuplot, edgecolors='none',s=1)
  # plt.title('通道R')
  #
  # #子图3
  # plt.subplot(223)
  # plt.scatter(G_Rxy[3],G_Rxy[4],s=1,c='green')
  # plt.title('通道G')
  # #子图4
  # plt.subplot(224)
  # plt.scatter(B_Rxy[3],B_Rxy[4],s=1,c='blue')
  # plt.title('通道B')
  # plt.show()

  return R_Rxy[0:3],G_Rxy[0:3],B_Rxy[0:3]


def main():
  img='./lena.jpeg'
  img1='./lena_encrypt1.png'
  img2='./lena_encrypt2.png'
  R_Rxy,G_Rxy,B_Rxy=correlation(img)
  #输出结果保留四位有效数字
  print("******该图像的各通道各方向的相关系数为*****")
  print('通道\tHorizontal\tVertical\tDiagonal')
  print(' R    \t{:.4f}    {:.4f}    {:.4f}'.format(R_Rxy[0],R_Rxy[1],R_Rxy[2]))
  print(' G    \t{:.4f}    {:.4f}    {:.4f}'.format(G_Rxy[0],G_Rxy[1],G_Rxy[2]))
  print(' B    \t{:.4f}    {:.4f}    {:.4f}'.format(B_Rxy[0],B_Rxy[1],B_Rxy[2]))

if __name__== '__main__':
  main()