【LeetCode 热题 HOT 100】题解笔记 —— Day03

? 作者主页：欢迎来到我的技术博客😎
? 个人介绍：大家好，本人热衷于Java后端开发，欢迎来交流学习哦！(￣▽￣)~*
🍊 如果文章对您有帮助，记得关注、点赞、收藏、评论??????
📣 您的支持将是我创作的动力，让我们一起加油进步吧！！！🎉🎉

一、全排列

1. 题目描述

2. 思路分析

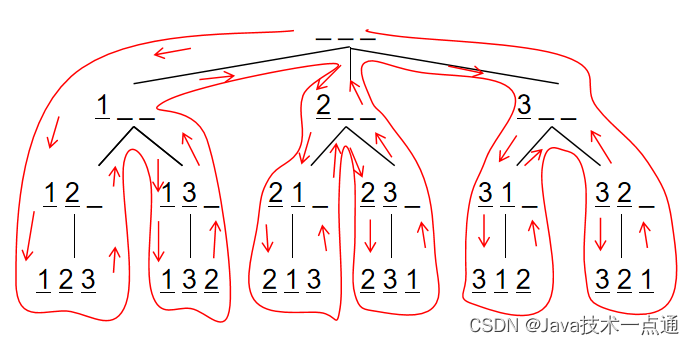
算法流程：

• 用 $path$ 数组来保存排序，当排序长度为 n 时，是一个排序方案，输出该方案；
• 用 $state$ 数组表示数字是否使用过。当 $state[i]$ 为 1 时表示 $i$已经被使用过，$state[i]$ 为 0 时表示 $i$没有被使用过；
• $dfs(i)$ 表示的含义是：在 $path[i]$ 处填写数字，然后递归的在下一个位置填写数字;
• 回溯：第 i 个位置填写某个数字的所有情况都遍历后， 第 i 个位置填写下一个数字。

---

3. 代码实现

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> path;
    vector<bool> st;

    vector<vector<int>> permute(vector<int>& nums) {
        path = vector<int>(nums.size());
        st = vector<bool>(nums.size());

        dfs(nums, 0);
        return ans;
    }

    void dfs(vector<int>& nums, int u) {
        if (u == nums.size()) {
            ans.push_back(path);
            return;
        }

        for (int i = 0; i < nums.size(); i ++) {
            if (!st[i]) {
                path[u] = nums[i];
                st[i] = true;
                dfs(nums, u + 1);
                st[i] = false;
            }
        }
    }
};

---

二、旋转图像

1. 题目描述

---

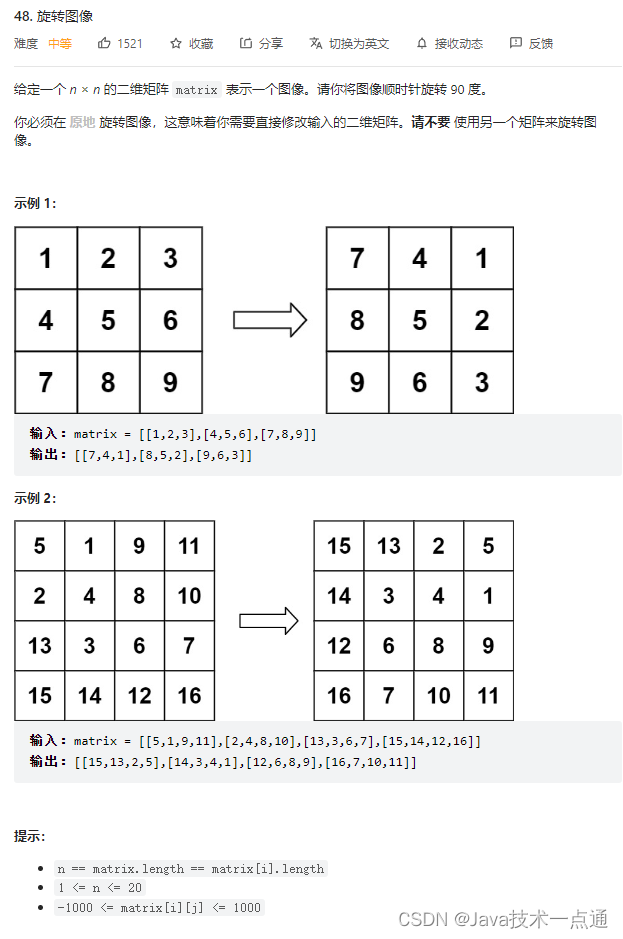
2. 思路分析

(操作分解） O($n^2$)
直接操作旋转$90^o$比较困难，我们可以将它分解成两个操作：

1. 先以左上-右下对角线为轴做翻转；
2. 再以中心的竖线为轴做翻转；

---

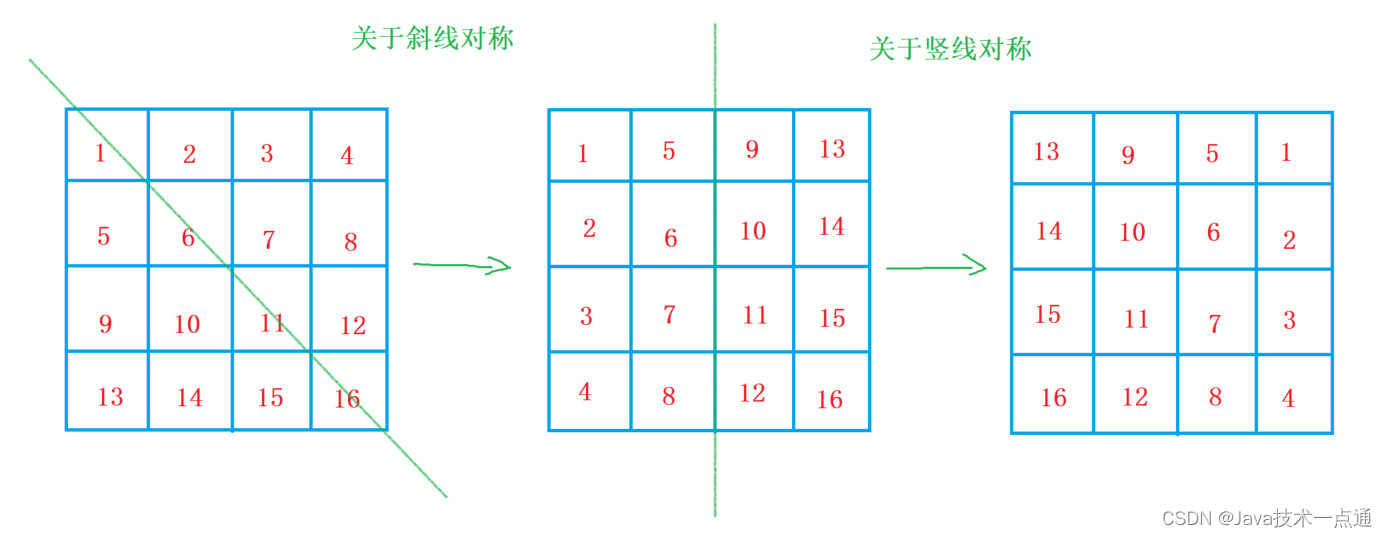
3. 代码实现

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n; i ++) 
            for (int j = i + 1; j < n; j ++)
                swap(matrix[i][j], matrix[j][i]);
        
        for (int i = 0; i < n; i ++)        
            for (int j = 0, k = n - 1; j < k; j ++, k --) 
                swap(matrix[i][j], matrix[i][k]);
    }
};

---

三、字母异位词分组

1.题目描述

---

2. 思路分析

由于互为字母异位词的两个字符串包含的字母相同，因此对两个字符串分别进行排序之后得到的字符串一定是相同的，故可以将排序之后的字符串作为哈希表的键。

定义从 string 映射到vector<string>的哈希表： unordered_map<string, vector<string>>。
我们将每个字符串的所有字符从小到大排序，将排好序的字符串作为key，然后将原字符串插入key对应的vector<string>>中

---

3. 代码实现

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        unordered_map<string, vector<string>> hash;
        for (auto& str : strs) {
            string nstr = str;
            sort(nstr.begin(), nstr.end());
            hash[nstr].push_back(str);
        }

        vector<vector<string>> res;
        for (auto& item : hash) res.push_back(item.second);

        return res;
    }
};

---

四、最大子数组和

1. 题目描述

---

2. 思路分析

动态规划 $O(n)$

1. 设 f(i)f(i) 表示以第 $i$ 个数字为结尾的最大连续子序列的 总和 是多少。
2. 初始化: f(0)=nums[0]。
3. 转移方程 f(i)=max(f(i?1)+nums[i],nums[i])。可以理解为当前有两种决策，一种是将第 $i$ 个数字和前边的数字拼接起来；另一种是第 $i$ 个数字单独作为一个新的子序列的开始。
4. 最终答案为 $ans=max(f(k)),0\le k<n$。

---

3. 代码实现

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size(), res = nums[0];
        vector<int> f(n);
        f[0] = nums[0];

        for (int i = 1; i < n; i ++) {
            f[i] = max(f[i - 1] + nums[i], nums[i]);
            res = max(res, f[i]);
        }
        return res;
    }
};

---

五、跳跃游戏

1. 题目描述

---

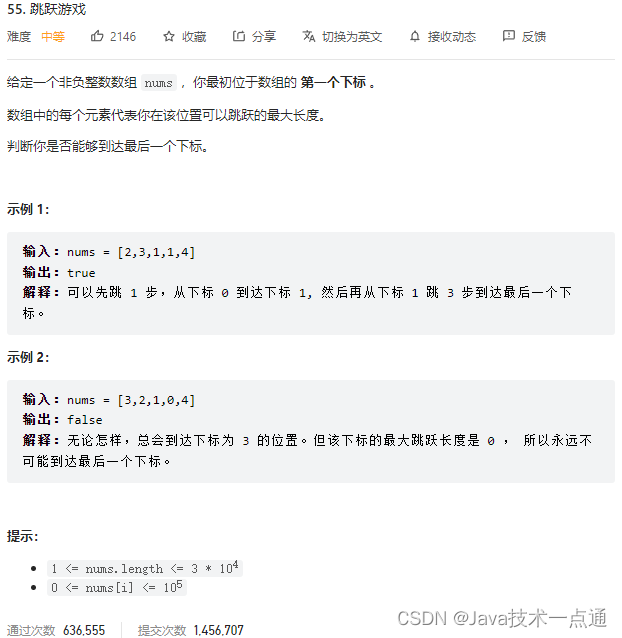
2. 思路分析

核心思想：尽可能跳到更远的位置。

1. 若往后的位置能跳到，则前面的位置一定可以跳到，$last$ 表示的是从前 $i?1$ 个位置中跳，能跳到最远的位置是 $last$；
2. 若前 $i?1$ 个位置中跳，跳到最远的位置是 $last$ 比 $i$ 小，表示从前 $i?1$ 个位置中跳，跳不到 $i$ 的位置，因此一定不能跳到最后一个的位置；
3. 若前 $i?1$ 个位置中跳，能跳到 $i$，则继续尝试从 $i$ 位置跳，可能会跳得更远，更新 $last$ 的值。

---

3. 代码实现

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int last = 0;
        for (int i = 0; i <nums.size(); i ++) {
            if (last < i) return false;
            last = max(last, i + nums[i]);
        }
        return true;
    }
};

六、合并区间

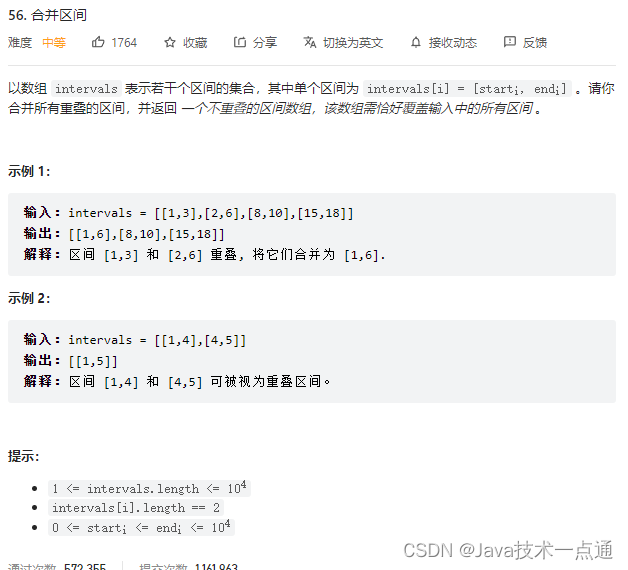
1. 题目描述

---

2. 思路分析

贪心思想：

1. 首先对各区间进行排序；
2. 定义当前区间的左右端点为第一个区间的左右端点；
3. 从前往后遍历每一个区间，如果当前区间与上一个区间有交集，则更新右端点；否则将上一个区间加入集合，然后更新当前区间。

---

3. 代码实现

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& a) {
        vector<vector<int>> res;
        if (a.empty()) return res;

        sort(a.begin(), a.end());
        int l = a[0][0], r = a[0][1];
        for (int i = 1; i < a.size(); i ++) {
            if (a[i][0] > r) {
                res.push_back({l, r});
                l = a[i][0], r = a[i][1];
            } else r = max(r, a[i][1]);
        }
        res.push_back({l, r});
        return res;
    }
};

---

七、不同路径

1. 题目描述

---

2. 思路分析

动态规划

1. 状态表示： f[i][j] 表示从起点到 $(i,j)$ 的路径总和；
2. 状态转移方程： f[i][j] = f[i - 1][j] + f[i][j - 1];
3. 初始化： 对于第一行f[0][j] 或者第一列 f[j][0]，由于都是在边界，所有只能为1。

---

3. 代码实现

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> f(m, vector<int>(n));

       for (int i = 0; i < m; i ++)
            for (int j = 0; j < n; j ++) {
                if (!i || !j) f[i][j] = 1; //f[i][0] 和 f[0][j]单独初始化为1
                else f[i][j] = f[i - 1][j] + f[i][j - 1];
            }
        return f[m - 1][n - 1];
    }
};

---

八、最小路径和

1. 题目描述

---

2. 思路分析

状态表示: f[i][j] 表示从起点到 $(i,j)$ 的最小路径和。
很显然，f[0][0] = grid[0][0]，对于 $f$ 中的其余元素值，通过以下状态转移方程计算元素值：

• 当 $i>0$ 且 $j=0$ 时(即第一行)，f[i][0] = f[i - 1][0] + grid[i][0];
• 当 $i=0$ 且 $j>0$ 时(即第一列)，f[0][j] = f[0][j - 1] + grid[0][j];
• 当 $i>0$ 且 $j>0$ 时，f[i][j] = min(f[i - 1][j], f[i][j - 1] + grid[i][j];

---

3. 代码实现

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();

        vector<vector<int>> f(n, vector<int>(m));
        f[0][0] = grid[0][0]; //起点

        //第一行，只能从左边来
        for (int i = 1; i < n; i ++) {
            f[i][0] = f[i - 1][0] + grid[i][0];
        }
        
        //第一列，只能从上面来
        for (int j = 1; j < m; j ++) {
            f[0][j] = f[0][j - 1] + grid[0][j];
        }

        //其他的则可以从左边或者上面来
        for (int i = 1; i < n; i ++) 
            for (int j = 1; j < m; j ++) {
                f[i][j] = min(f[i - 1][j], f[i][j - 1]) + grid[i][j];
            }
        
        return f[n - 1][m - 1];
    }
};

---

九、爬楼梯

1. 题目描述

---

2. 思路分析

定义数组 $f[i]$ 表示上 $i$ 级台阶的方案数，则枚举最后一步是上1级台阶，还是上2级台阶，所以有：f[i] = f[i ? 1] + f[i ? 2]。

---

3. 代码实现

class Solution {
public:
    int climbStairs(int n) {
        vector<int> f(n + 1);
        f[0] = 1;
        f[1] = 1;
        for (int i = 2; i <= n; i ++) 
            f[i] = f[i - 1] + f[i - 2];
        
        return f[n];
    }
};

---

十、编辑距离

1. 题目描述

---

2. 思路分析

动态规划
状态表示： f[i][j] 表示 $word1$ 到 $i$ 位置转化成 $word2$ 到 $j$ 位置需要的最小步数。

状态转移方程：

• 当 word1[i] == word2[j]，f[i][j] = f[i - 1][j - 1];
• 当 word1[i] != word2[j]，[i][j] = min(f[i - 1][j - 1] + 1, min(f[i][j - 1] + 1, f[i - 1][j] + 1));

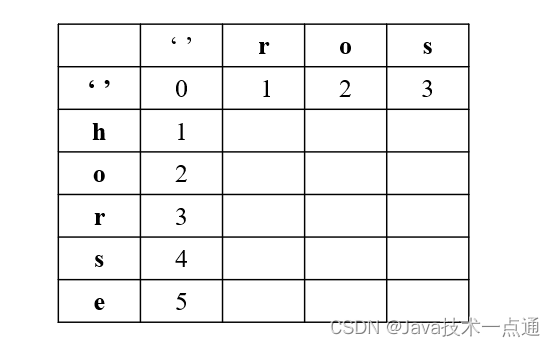
其中，f[i - 1][j - 1] 表示替换操作， f[i - 1][j] 表示删除操作，f[i][j - 1] 表示插入操作。

注意：针对第一行和第一列到单独考虑，我们引入 '' 如下图所示：

---

3. 代码实现

class Solution {
public:
    int minDistance(string a, string b) {
        int n = a.size(), m = b.size();
        a = ' ' + a, b = ' ' + b;
        vector<vector<int>> f(n + 1, vector<int>(m + 1));

        for (int i = 1; i <= n; i ++) f[i][0] = i;
        for (int j = 1; j <= m; j ++) f[0][j] = j;

        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= m; j ++) {
                if (a[i] == b[j]) 
                    f[i][j] = f[i - 1][j - 1];
                else
                    f[i][j] = min(f[i - 1][j - 1] + 1, min(f[i][j - 1] + 1, f[i - 1][j] + 1));
            }
        return f[n][m];
    }
};

---

?
非常感谢您阅读到这里，如果这篇文章对您有帮助，希望能留下您的点赞👍 关注💖 分享👥 留言💬thanks！！！