序列模型（4）—— Scaling Laws

• 本文介绍 LLM 训练过程中重要的 Scaling Laws，这是一个经验规律，指出了固定训练成本（总计算量FLOPs）$C$ 时，如何调配模型规模（参数量）$N$ 和训练 Token 数据量 $D$，才能实现最高的效率。利用 Scaling Laws，我们可以利用较小模型的训练经验预测更大模型的性能表现
• 本文主要是对论文 Scaling Laws for Neural Language Models 的解析，只关注汇总结果的话可以直接看第 5 节
  • 文章链接：Scaling Laws for Neural Language Models
  • 发表：arxiv 2020
  • 作者：OpenAI

---

• 摘要：我们研究了 LM 在交叉熵损失上的经验缩放规律（empirical scaling laws）。（测试）损失随着模型大小、数据集大小和训练计算量的增加呈幂律减小，有时这种趋势可以横跨七个数量级以上；相比而言，网络宽度或深度等其他架构细节在较大范围内几乎没有影响。过拟合与模型规模/数据集大小的依赖关系、训练速度与模型大小的依赖关系都可以用简单的方程进行描述，这些关系使我们能够确定计算量预算的最佳分配方式。较大模型具有更高的样本效率，因此在最高效的计算训练中，应该在相对较少的数据上训练非常大的模型，并在收敛之前很久停止训练（stopping significantly before convergence）

0. 背景和方法

0.1 Transformer 模型的参数量和计算量

• 原文符号有点乱，直接引用前文的分析结论，详见：序列模型（3）—— LLM的参数量和计算量。首先给出符号约定

  参数	符号	说明
  Decoder 层数	$l$
  Token 嵌入维度	$d$
  Attention 层嵌入维度	$d$
  MLP 隐藏层维度	$4d$	通常设置为嵌入维度4倍
  Attention head 数量	$n$	要求其整除 $d$
  词表尺寸	$V$
  模型输入长度	$s$	代表模型处理的上下文长度
  训练 batch data	$x$	张量尺寸 ${\mathbb{R}}^{B\times s\times d}$
  训练步数	$S$	即模型参数更新次数
  交叉熵损失	$L$	本文中主要指测试损失，可用于指示模型性能
  batch_size	$B$
  模型参数量	$N$
  训练数据量（Token）	$D$
  训练计算量（FLOPs）	$C$
  损失的幂律指数	${\alpha }_X$	Scaling Laws 就是 $L(X)\propto 1/X^{\alpha x}$，其中 $X$ 可以是 $N,D,C$ 之中的任意一个

• Decoder-only Transformer 模型的参数量 $N$、计算量 $C$ 和数据量 $D$ 之间有以下关系

  • 模型总参数量近似为 $N\approx 12l{d}^2$
  • 对于一次训练迭代过程，输入 token 数据量为 $D=Bs$，总计算量（FLOPs）近似为 $C\approx 72Bsl{d}^2$
  • 训练过程中，$N,C,D$ 之间有关系 $C\approx 6ND$

0.2 实验方法

• 模型：主要考察 Decoder-only Transformer 模型（GPT1），同时也对 Encoder-Decoder Transformer 模型（Universal transformers）和 LSTM 等传统序列模型进行了小规模实验。除非特殊说明，则上下文长度固定为 1024
• 数据集：使用 WebText2 数据集进行训练，它使用字节对编码进行分词，词表大小为 50257
• 训练方法：
  • 优化自回归交叉熵损失（损失具体设计为一条轨迹上所有 token 预测交叉熵损失的平均值）
  • 除非专门说明，使用 Adam 优化器进行训练 $2.5\times 10^5$ 步，$B=512,s=1024$
  • 除非专门说明，所有训练过程的学习率调度为：3000 步线性预热，然后余弦衰减至 0
• 实验设置：为了考察语言模型的缩放规律，作者在大量不同设置下进行训练，调整的参数包括
  • 模型规模：参数量 $N$ 从 768 到 15 亿不等（不含嵌入层参数）
  • 数据集大小：Token 数量 $D$ 从 2200 万到 230 亿
  • 模型形状：调整深度、宽度、注意力头和前馈维度等的设计，并维持总参数量基本不变
  • 上下文长度：大多数训练中为 $s=1024$，但也会尝试了更短的上下文
  • 批量大小：大多数训练中为 $2^{19}$

1. Basic Power Laws

1.1 模型形状基本不影响性能

• 当保持模型规模 $N$ 固定时，Transformer 性能对模型深度，注意力头数和前馈网络宽度等的依赖性非常弱
  

1.2 参数量和性能呈现幂律关系

• 作者通过调整模型层数 $l$ 和嵌入维度 $d$ 设置了一系列不同参数规模的模型，参数范围从小模型 $(l,d)=(2,128)$ 到具有十亿参数规模的大模型，形状从 $(6,4288)$ 到 $(207,768)$，所有模型都训练到接近收敛，并确保没有观测到过拟合
  
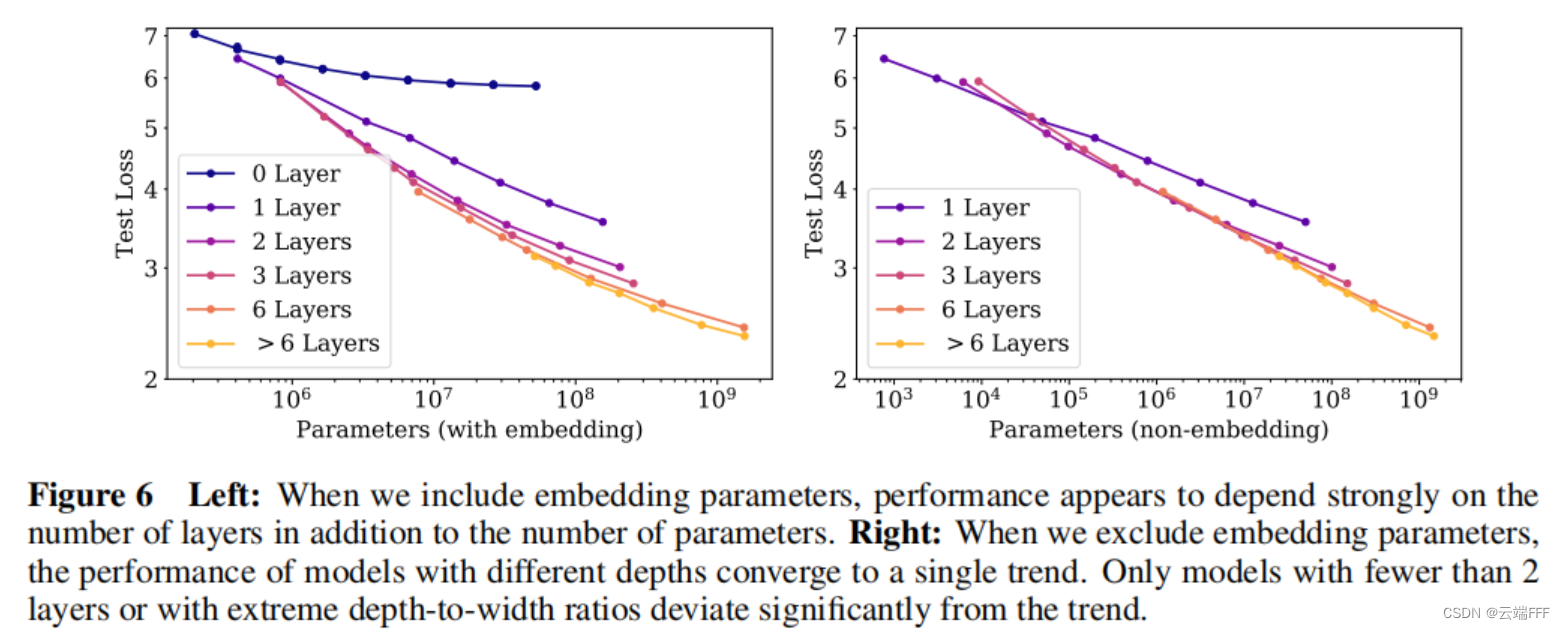
• 如图所示，注意到考虑嵌入层参数时，模型深度也会在总参数量之外影响性能规律；不考虑嵌入层参数时，性能和总参数量 $N$ 具有稳定的幂律关系，可以表示为
  $$L(N)\approx {\left(\frac{N_c}{N}\right)}^{{\alpha }_N}$$

  • 作者进一步考察了其他序列模型以及模型的泛化性能
    1. 作者验证了 LSTM 和 Encoder-Decoder 类模型都服从以上幂律关系
       
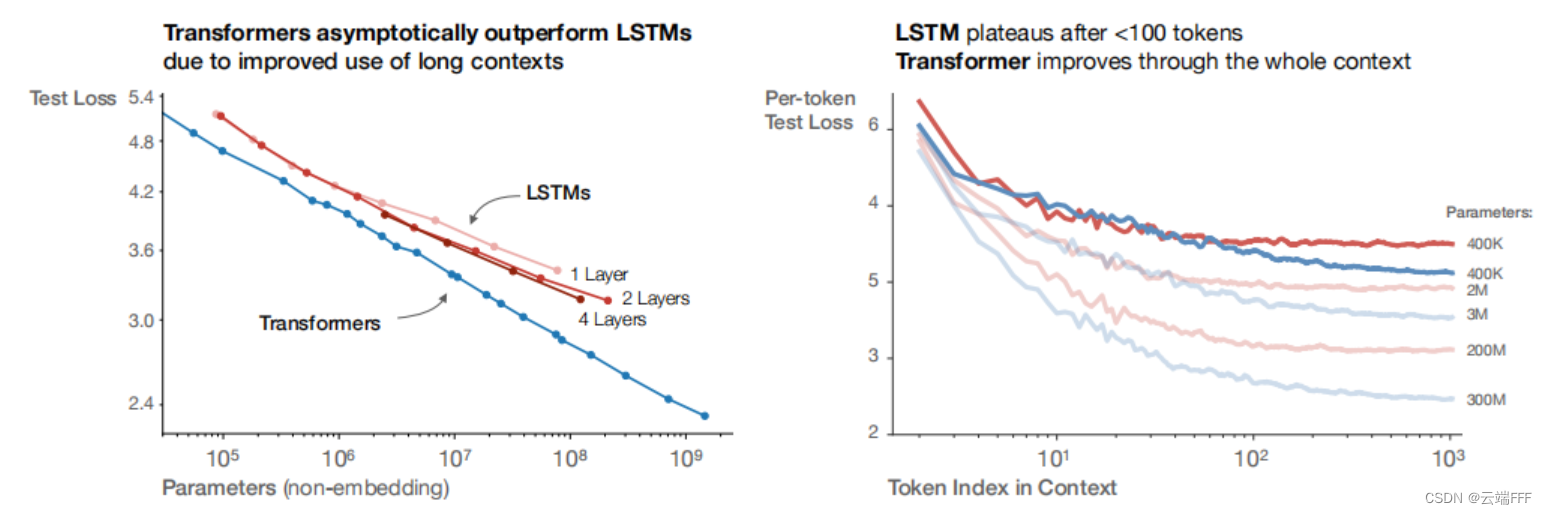
       左图显示了 LSTM/Transformer 模型的参数规模与性能间的幂律关系，从中也可发现 Transformer 模型总能用较少的参数量实现更好的性能；右图显示了上下文长度和预测性能的关系，可见 LSTM 仅在早期 Token 部分和 Transformer 模型性能类似，长跨度下性能不如 Transformer
       
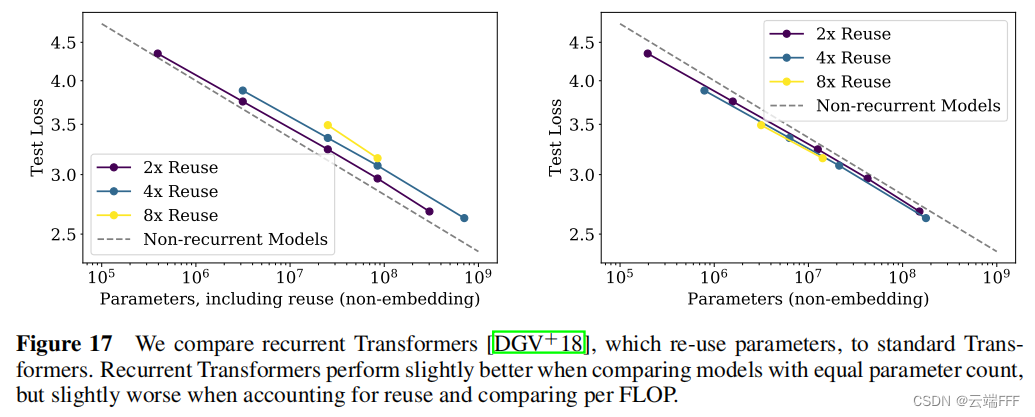
       这里考察的是带有递归循环和参数复用结构的 Encoder-Decoder Transformer 模型 Universal Transformers，可见参数量和性能间也满足幂律关系
    2. 作者验证了模型泛化性能也服从以上幂律关系
       
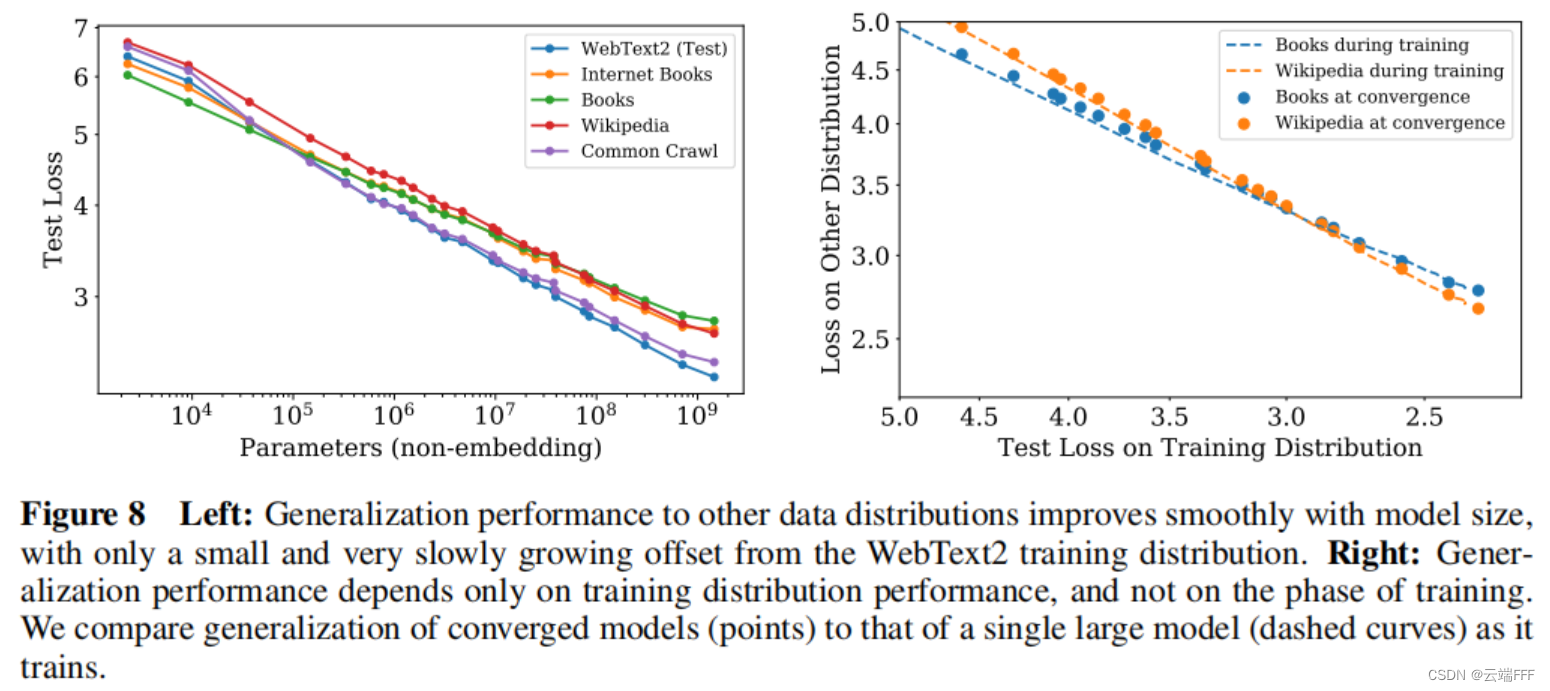
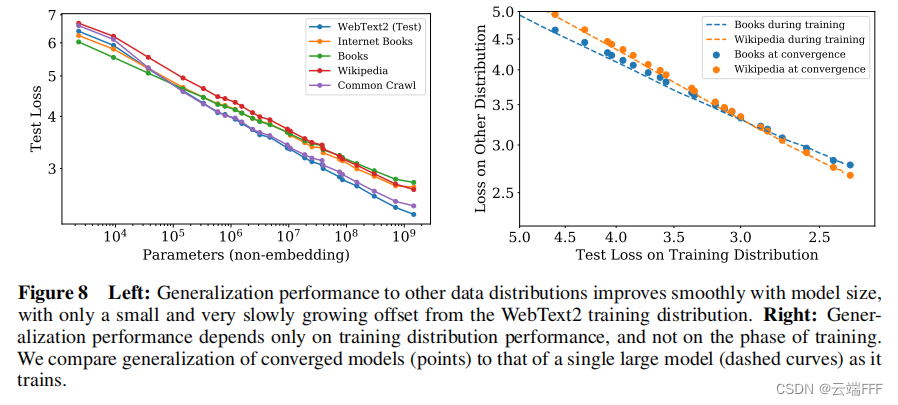
       左图显示了在 WebText2 上训练模型，然后在多种数据集上测试的泛化性能表现，显示出一致的幂律关系；右图说明泛化性能仅取决于训练分布上的性能，而与训练阶段无关

1.3 数据量 & 计算量和性能呈现幂律关系

• 作者发现数据量 & 计算量也都和模型性能呈现幂律关系，如下所示
  

  • 考察计算量 $C$ 与性能的关系时（左图），作者先用充足的数据训练多种不同参数规模 $N$ 的模型只收敛，然后对任意给定的 $C$，考察所有模型，找到第 $S=\frac{C}{6NB}$ 步时最优的模型性能绘制（为此需保持所有模型训练时 $B$ 不变，我们将在第 4 节进一步讨论更高效的训练方案）。注意到幂律关系
    $$L(C)\approx {\left(\frac{C_c}{C}\right)}^{{\alpha }_C}$$

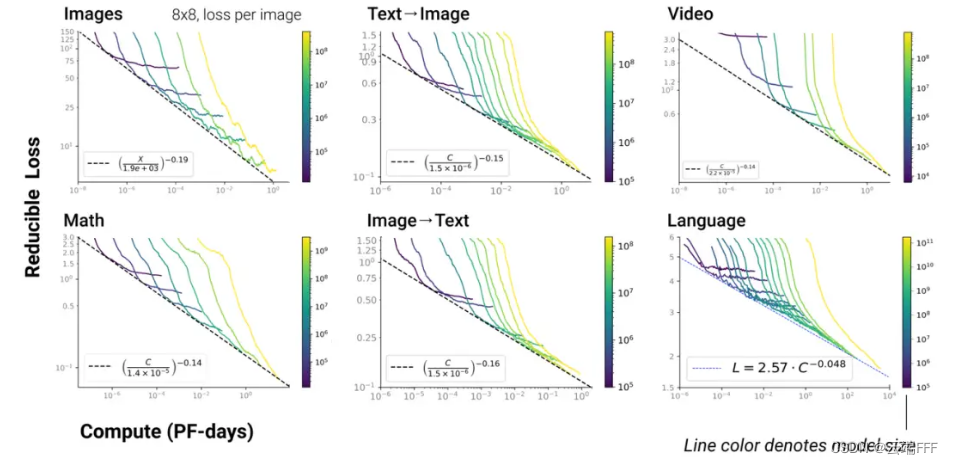
    • 值得注意的时，以上幂律关系在 LLM 多模态任务中依然存在
      

  • 考察数据量 $D$ 与性能的关系时（中图），作者训练规模为 $(l,d)=(36,1280)$ 的模型直到收敛。注意到幂律关系
    $$L(D)\approx {\left(\frac{D_c}{D}\right)}^{{\alpha }_D}$$

2. 利用 Scaling Laws 计算避免过拟合所需的数据量

• 第一节分析的三个幂律关系 $L(C),L(D),L(N)$ 都是单独考察的，即考察一个量时，总是调整其他两个量的取值，使模型性能仅受被考察的量影响
• 本节中，进一步考察模型性能如何同时受到 $N$ 和 $D$ 两个量的影响，这可以指导我们如何在控制过拟合的情况下，考察训练模型所需的数据量

2.1 参数量 $N$ 和数据量 $D$ 对模型性能的联合影响

• 基于第一节发现的幂律关系，作者直接将 $L(N,D)$ 的表达式假设为
  $$L(N,D)={\left[{\left(\frac{N_c}{N}\right)}^{\frac{{\alpha }_N}{{\alpha }_D}}+\frac{D_c}{D}\right]}^{{\alpha }_D}$$ 此设计很好地适配了数据，其形式基于以下三个原则
  1. 词表大小或 tokenize 方法的变化应当会对损失值进行整体的缩放（rescale the loss by an overall factor），这种缩放需要被自然地考虑到

     该设计中我们可以通过调节 $N_c,D_c$ 来适应这些变化

  2. 固定 $D$，$N\to \infty$ 时应有 $L(N,D)\to L(D)$；固定 $N$，$D\to \infty$ 时应有 $L(N,D)\to L(N)$

     有限的 $D$ 下，任何模型都无法接近最佳损失（即文本的熵）；同样固定大小 $N$ 的模型将受到容量限制。另一方面，有 $L(\infty ,D)=L(D),L(N,\infty )=L(N)$

  3. $L(N,D)$ 应该在 $D\to \infty$ 时进行分析（通常有足够的数据训练模型），这时它应具有以整数次幂的 $\frac{1}{D}$ 为变量的级数展开（即形如 $f(D)=a_0+\frac{a_1}{D}+\frac{a_2}{D^2}+...$），因此以上设计中 $N$ 和 $D$ 并不完全对称

     这个原则更具推测性，由于过拟合应该与数据集的方差或信噪比相关，而它们按 $\frac{1}{D}$ 成比例缩放，所以我们通常期望过拟合在非常大的 $D$ 下也成比例于 $\frac{1}{D}$ 进行缩放。这个期望对于任何平滑的损失函数都应该成立。然而，这假设 $\frac{1}{D}$ 的修正项在方差的其他来源（如有限 batch size）上占主导地位，这还没有经验证实

• 利用以上定义，可以将模型的过拟合程度形式化表示为
  $$\begin{array}{rl}\delta L(N,D)& \equiv \frac{L(N,D)}{L(N,\infty )}?1\\ & \approx {\left(1+{\left(\frac{N}{N_c}\right)}^{\frac{{\alpha }_N}{{\alpha }_D}}\frac{D_c}{D}\right)}^{{\alpha }_D}?1\end{array}$$ 这意味着模型的过拟合程度和 $N^{\frac{{\alpha }_N}{{\alpha }_D}}/D$ 成幂律关系

2.2 实验验证

• 作者用 10% 的 dropout 对所有模型进行正则化，训练直到测试损失不再下降（早停策略），结果如下所示
  
  • 左图：对于较大的 $D$，性能表现出关于 $N$ 的幂律关系；对于较小的 $D$，随着 $N$ 的增加模型开始过拟合。虚线是拟合结果，验证了以上定义的有效性
  • 右图：考察过拟合情况，实线拟合了 $N^{\frac{{\alpha }_N}{{\alpha }_D}}/D$ 和过拟合程度间的幂律关系，验证了以上定义的有效性

2.3 预测数据集尺寸以避免过拟合

• 利用大量小规模实验的结果，可以拟合出当 Scaling Laws 中的一些关键常数，这里为
  
  设不同随机种子下的验证损失变化约为 2%，这意味着在训练达到我们所需的收敛阈值时，避免过拟合需要
  $$D\ge \left(5\times 10^3\right)N^{0.74}$$ 通过这种关系，可在 token 数据量 $D$ 为 22B 的数据集上以最小的过拟合训练参数量 $N$ 不超过 $10^9$ 的模型
• 这一节的重要意义在于给出了一种利用 Scaling Laws 进行预测的思路，即首先进行大量小规模实验，然后用基于 Scaling Laws 的关系式对结果进行拟合，最后用拟合曲线预测更大规模模型的情况

3. 模型大小和训练时间的缩放定律

• 现在我们讲起 Scaling Laws 时，主要关注的通常就是前两节（特别是第一节）所述内容。但是原始论文中还进行了进一步分析，使其更符合现实情况。在进一步分析之前，首先引入一些新符号

  参数	符号	说明
  关键 batch size	$B_{\text{crit}}$	以此 batch size 进行训练大致上在时间和计算效率之间提供了一个最优的折衷
  最小计算量	$C_{\min }$	达到给定损失值最小计算量，这是模型以远小于 $B_{\text{crit}}$ 的 batch size 训练时的计算量
  最小训练步骤	$S_{\min }$	达到给定损失值的最小训练步数。这是模型以远大于 $B_{\text{crit}}$ 的 batch size 训练时的步数
  最小处理数据量（Token）	$E_{\min }$	达到给定损失值所处理的最小数据量

• 设置过大的 batch size 会影响计算效率，因为足够大的 batch size 下计算的梯度方向已经足够准确，继续加大的意义不大。一般认为训练过程中存在一个临界 batch size $B_{\text{crit}}$：当 $B\le B_{\text{crit}}$ 时，加大 $B$ 对计算效率无明显影响；当 $B>B_{\text{crit}}$ 时，加大 $B$ 会使得计算效率下降。

  • 以 $B\approx B_{\text{crit}}$ 进行训练可以最大化训练的计算效率，即到达相同性能用时最短
  • 以 $B?B_{\text{crit}}$ 进行训练可以最小化训练步骤数量，$S\to S_{\min }$，但达相同性能耗时更长
  • 以 $B?B_{\text{crit}}$ 可以最小化计算量，$C\to C_{\min }$，但达相同性能耗时更长

3.1 拟合 $B_{\text{crit}}(L)$, $S_{\min }(S)$ 和 $C_{\min }(C)$

• 作者通过实验发现，为了达成任意固定的性能损失 $L$，训练步数 $S$ 和训练处理数据量 $E=BS$ 之间存在反比例关系
  
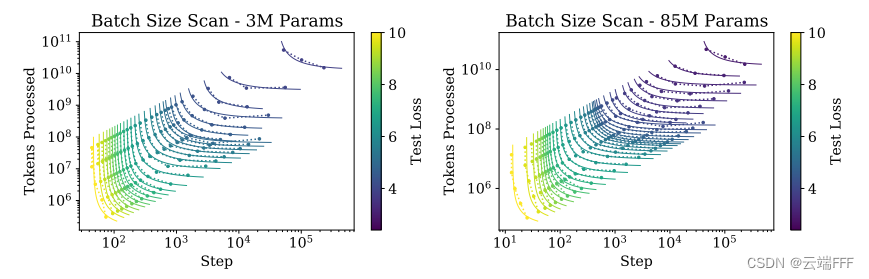
  如图所示，作者使用不同参数量的两个 Transformer 模型，考察达到指定性能损失（颜色表示）所需的训练步数 $S$ 和处理 Token 数量 $E$ 之间的关系。图像说明，为了达成固定的 $L$，随着 $S$ 增大，所需处理的 Token 数量 $E$ 在减少
  1. 为了达成固定的 $L$，从左到右训练步数 $S$ 越多，处理的 Token 数量 $E$ 越少，$B$ 越小，总计算量 $C$ 越小
  2. 注意到每一条线都呈现反比例关系，作者提出它们服从如下关系
     $$\left(\frac{S}{S_{\min }}?1\right)\left(\frac{E}{E_{\min }}?1\right)=1$$ 注意到这本质就是一个反比例函数，两个 $?1$ 是把坐标轴移动到曲线所在位置
• 每一条线最左边的点对应 $B_{\max }=\frac{E_{\max }}{S_{\min }}$，最右边的点对应 $B_{\min }=\frac{E_{\min }}{S_{\max }}$，它们对应训练效率的两个低点，$B_{\text{crit}}$ 应该在二者之间，作者将其定义为
  $$B_{\text{crit?}}(L)\equiv \frac{E_{\min }}{S_{\text{min?}}}$$ 作者发现这种定义和另一种可以估计 $B_{\text{crit?}}$ 的方法 “噪声梯度度量” 得到的结果类似。根据拟合情况，以 $B_{\text{crit?}}$ 训练大约需要 $2S_{\min }$ 的训练步骤和 $2E_{\min }$ 的数据量
• 作者通过实验验证了 $B_{\text{critc}}$ 也和模型性能（用损失表示）之间呈现幂律关系
  
  如图可见，$B_{\text{crit?}}(L)$ 仅和性能 $L$ 相关，而与模型规模等其他因素无关。作者将幂律关系表示为为
  $$B_{\text{crit?}}(L)\approx \frac{B_{?}}{L^{1/{\alpha }_B}}$$ 其中 $B_{?}$ 和 ${\alpha }_B$ 是需要拟合的参数，这种表示可以使 $B_{\text{crit?}}(L)$ 的估计值在 $L\to 0$ 时发散，以保持和另一种估计方法 “噪声梯度度量” 的一致性。
• 给定任意训练过程参数 $C,N,B,S$，如前文所述它们之间满足 $C\approx 6NBS$，设该训练过程达成的性能（损失表示）为 $L$，可以借助 $B_{\text{crit}}$ 表示出达成相同 $L$ 对应的 $S_{\min }$ 和 $C_{\min }$
  $$\begin{array}{rlrl}& S_{\min }(S)\equiv \frac{S}{1+B_{\text{crit?}}(L)/B}& & \left(\text{?minimum?steps,?at?}B?B_{\text{crit?}}\right)\\ & C_{\min }(C)\equiv \frac{C}{1+B/B_{\text{crit?}}(L)}& & \text{?(minimum?compute,?at?}B?B_{\text{crit?}}\text{)}\end{array}$$ 总体上可以看出就是按上面的反比例关系调整了一下，但具体为什么如此调整定义说实话有点没看懂。由于 $B_{\text{crit}}(L)$ 可以拟合表示，这里的 $S_{\min }(S)$ 和 $C_{\min }(C)$ 也都可以拟合表示了

3.2 拟合 $L(N,S)$

• 作者通过实验验证了，在无数据量限制的情况下，对给定参数量 $N$ 的模型以足够大的 batch size 训练 $S_{\min }$ 步之后，如下右图所示
  
  模型性能与 $N$ 和 $S_{\min }$ 之间存在以下幂律关系关系
  $$L\left(N,S_{\min }\right)={\left(\frac{N_c}{N}\right)}^{{\alpha }_N}+{\left(\frac{S_c}{S_{\min }}\right)}^{{\alpha }_S}$$ 再配合上一节中 $S_{\min }$ 的定义，在无数据限制的情况下对参数量为 $N$ 的模型训练 $S$ 步后得到的性能可以用下式拟合
  $$L\left(N,S\right)={\left(\frac{N_c}{N}\right)}^{{\alpha }_N}+{\left(\frac{S_c}{S_{\min }(S)}\right)}^{{\alpha }_S}$$
• 作者进一步在无数据限制的情况下拟合了不同参数量 $N$ 下性能和计算量 $C$ 以及训练步数 $S$ 的关系
  
  良好的拟合结果也验证了以上提出 $L\left(N,S\right)$，$S_{\min }(S)$ 和 $C_{\min }(C)$ 等表达式的有效性

4. 计算量的优化分配

• 第 1 节已经分析了，在不考虑 $N$ 和 $D$ 限制的情况下，计算量 $C$ 与性能的之间存在幂律关系
  $$L(C)\approx {\left(\frac{C_c}{C}\right)}^{{\alpha }_C}$$ 但是这个结果的前提是以固定 batch size $B$ 进行训练，事实上，我们可以按第 3 节所述的 $B_{\text{crit}}$ 进行训练，从而提高训练效率。本节中我们进一步分析这种情况

• 作者首先对性能和 $C_{\min }$ 的关系进行拟合（不考虑 $N$ 和 $D$ 的约束），如下所示
  

  这里作者使用远低于 $B_{\text{crit?}}$ 的 batch size 训练以考察性能和 $C_{\min }$ 的关系。注意到 $C_{\min }$ 同样和性能间存在幂律关系 $L(C_{\min })$，但是具体的表达式和 $C$ 的幂律关系 $L(C)$ 有所区别

• 作者进一步考察可以最高效训练的最优模型参数量 $N(C_{\min })$，拟合结果如下所示
  
  如左图所示，最优参数量和最小计算量之间也存在幂律关系，拟合结果约为
  $$N(C_{\min })\propto C_{\min }^{0.73}$$ 进一步地，注意到
  $$\begin{array}{rlrl}& (3.1节拟合结果)& & B_{\text{crit?}}\propto L^{?4.8}\\ & (4.1节拟合结果)& & L\propto C_{\min }^{?0.05}\end{array}?B_{\text{crit?}}\propto C_{\min }^{0.24}$$ 又根据定义 $C_{\min }\equiv 6N(C_{\min })B_{\text{crit?}}S$，可以推出
  $$C_{\min }\propto 6C_{\min }^{0.73}{C}_{\min }^{0.24}S?S_{\min }\propto C_{\min }^{0.03}$$ 这个结果也和拟合结果相吻合，如上右图所示

  PS：这里说根据定义我觉得有点问题，因为根据定义 $C_{\min }$ 应该是在用远小于 $B_{\text{crit}}$ 的 batch size 训练得到的，这里应该是假设了这个小 batch size 仍然和 $B_{\text{crit}}$ 有相同的数量级

• 总之我们可以得出结论：当不受训练数据量限制时，随着总计算量的提高，存在有对应的最优模型规模（训练效率最高）
  
  我们应该以最佳的计算分配来扩大语言模型，即
  

  1. 主要按 $N(C_{\min })\propto C_{\min }^{0.73}$ 的幂律关系模型参数规模
  2. 通过 $B\propto B_{crit}$，即 $B\propto C_{\min }^{0.24}$ 来扩大 batch size
  3. 训练步数 $S$ 的增量可以忽略不计

5. 总结

• 本文只涵盖了原文中的核心结论，部分更进一步的分析假设比较强就没有写了，请参考原文。
• 下面对本文通过实验发现的 Scaling Laws 进行总结

  1. 模型性能与规模密切相关，与模型形状关系较弱：模型性能主要取决于模型参数量（不包括嵌入）$N$、数据集（Token）大小 $D$ 以及训练计算量（FLOPs）$C$。在合理范围内，性能对其他超参数（如深度与宽度的比例、训练学习率调度方案）的依赖程度很低

     
     

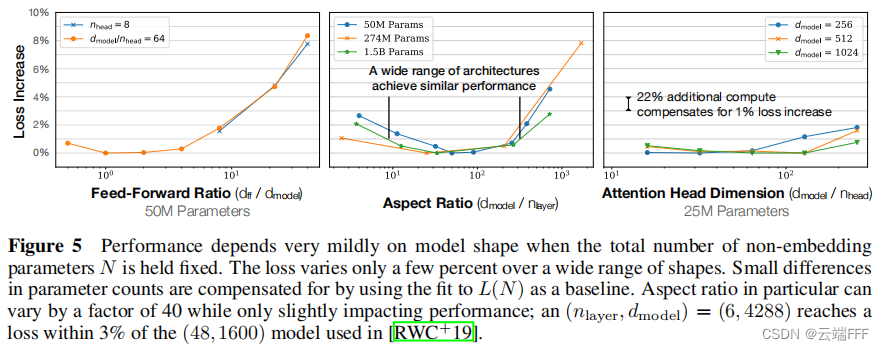
  2. 平滑的幂律关系：当不被其他两个因素限制时，模型性能与 $N$、$D$、$C$ 之间存在幂律关系，这种关系在很大范围内一直保持（跨越六个以上数量级）。这种幂律关系在 Decoder-Only Transformer、Encoder-Decoder Transformer、LSTM 等多种序列模型上都有体现，对于 NLP 以外的多模态任务也成立。

     

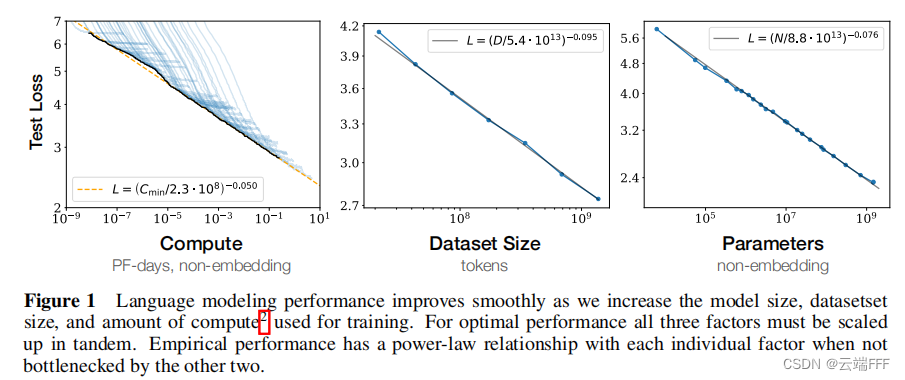
     通过在小模型上拟合以下幂律关系，可以外推预测大模型、大数据量和大计算量下的性能表现

     • 控制模型参数量 $N$，用足够数据训练至收敛，性能与 $N$ 的关系满足（不包含嵌入参数）
       $$L(N)\approx {\left(\frac{N_c}{N}\right)}^{{\alpha }_N}$$
     • 控制训练数据量 $D$，使用早停策略训练足够大的大规模模型，性能与 $D$ 的关系满足
       $$L(D)\approx {\left(\frac{D_c}{D}\right)}^{{\alpha }_D}$$
     • 控制训练计算量 $C_{\min }$，使用足够大的数据集对最优尺寸的模型，以足够小的 batch size 进行训练（此时计算量最小）时，性能与 $C_{\min }$ 满足
       $$L(C_{\min })\approx {\left(\frac{C_c^{\min }}{C_{\min }}\right)}^{{\alpha }_c^{\min }}$$

  3. 过度拟合的普遍规律：在不考虑训练数据量 $C$ 的限制时，只要同时扩大 $N$ 和 $D$，性能就会可预测地提高，但如果固定 $N$ 或 $D$ 中的一个而增加另一个，就会进入回报递减的领域。过拟合程度和 $N^{\frac{{\alpha }_N}{{\alpha }_D}}/D$ 之间存在幂律关系。这意味着每当模型大小 $N$ 增加 8 倍，将数据量 $D$ 增加 $8^{\frac{{\alpha }_N}{{\alpha }_D}}$ 倍就可以维持过拟合程度不增加

     

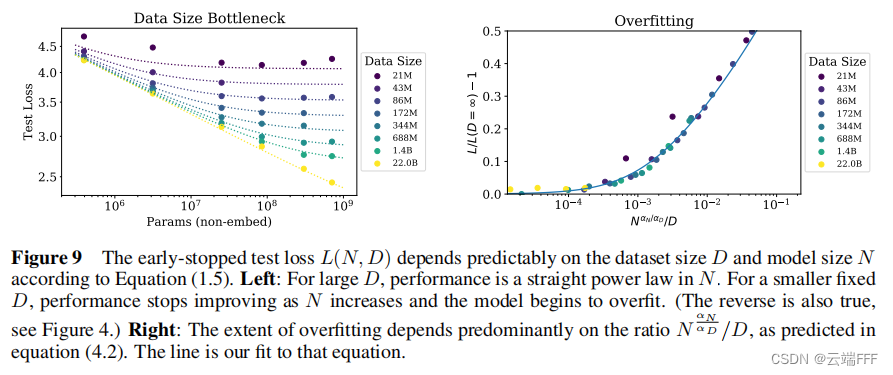
     不考虑训练计算量限制时，性能受到 $N$ 和 $D$ 的联合影响
     $$L(N,D)={\left[{\left(\frac{N_c}{N}\right)}^{\frac{{\alpha }_N}{{\alpha }_D}}+\frac{D_c}{D}\right]}^{{\alpha }_D}$$ 过拟合程度可以表示为
     $$\begin{array}{rl}\delta L(N,D)& \equiv \frac{L(N,D)}{L(N,\infty )}?1\\ & \approx {\left(1+{\left(\frac{N}{N_c}\right)}^{\frac{{\alpha }_N}{{\alpha }_D}}\frac{D_c}{D}\right)}^{{\alpha }_D}?1\end{array}$$ 这意味着过拟合程度和 $N^{\frac{{\alpha }_N}{{\alpha }_D}}/D$ 成幂律关系

  4. 训练的普遍规律：训练曲线遵循可预测的幂律，通过外推训练曲线的早期部分，我们可以大致预测如果我们训练更长时间会达到的损失

     

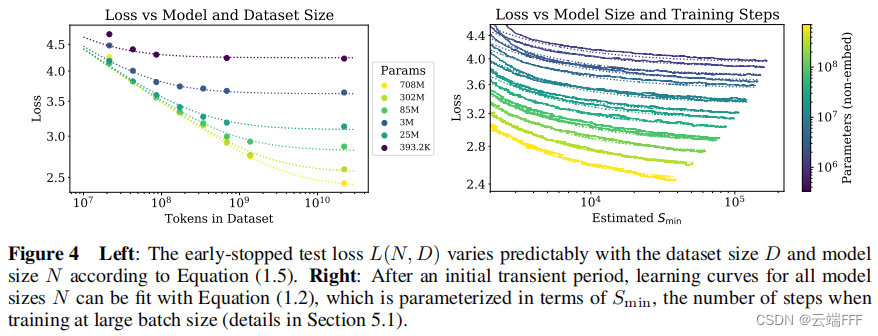
     在无数据限制的情况下，对参数量为 $N$ 的模型训练 $S$ 步后得到的性能可以用下式拟合
     $$L\left(N,S\right)={\left(\frac{N_c}{N}\right)}^{{\alpha }_N}+{\left(\frac{S_c}{S_{\min }(S)}\right)}^{{\alpha }_S}$$ 其中 $S_{\min }(S)\equiv \frac{S}{1+B_{\text{crit?}}(L)/B}\left(\text{?minimum?steps,?at?}B?B_{\text{crit?}}\right)$

  5. 迁移随着测试性能的提高而提高：当我们使用与训练数据不同的分布对文本进行模型评估时，结果与训练验证集上的结果高度相关，损失大致恒定。换句话说，迁移到不同的分布会导致恒定的损失，但其他方面会大致与训练集上的性能保持一致

     

  6. 样本效率：大型模型比小型模型更具样本效率，使用更少的优化步数和更少的数据点就能达到相同的性能水平

     

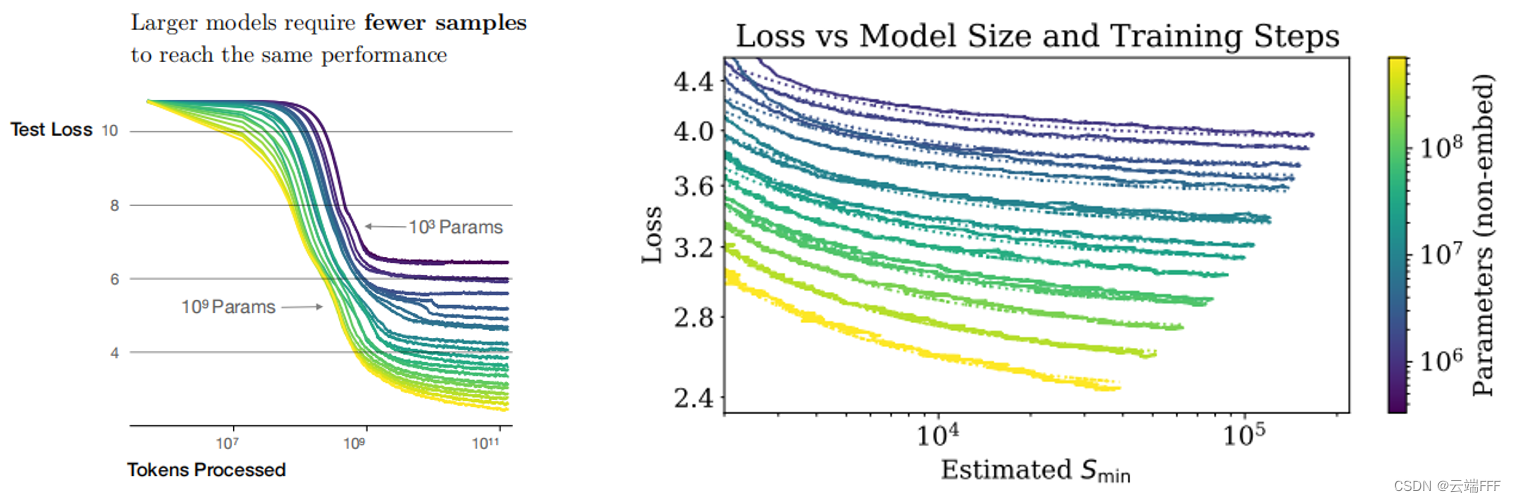
  7. 收敛效率低：随着 $C$ 的增大，为了达成最高训练效率，数据 $D$ 的增量要显著小于模型参数量 $N$ 的增量。因此当固定计算量预算 $C$ 而不限制模型大小 $N$ 和可用数据 $D$ 时，可以通过训练非常大的模型并在明显缺乏收敛性时停止来获得最佳性能，这比将小模型训练至收敛的训练效率高很多

     

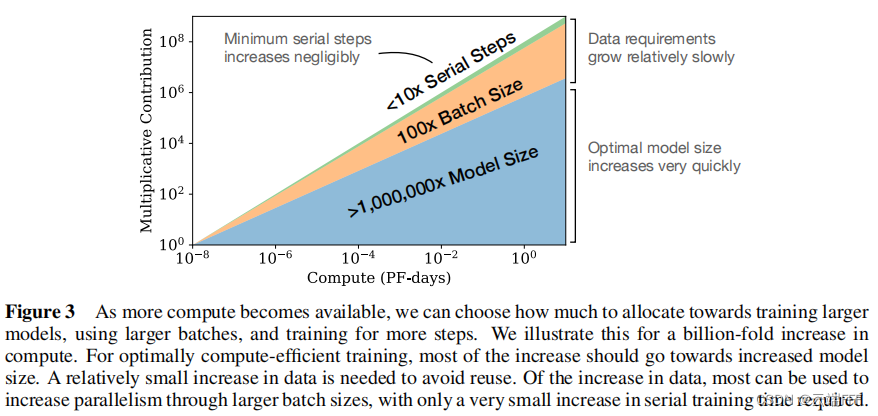
     当固定训练总计算量 $C$ 而没有其他任何限制时，可以基于 $L\left(N,S\right)={\left(\frac{N_c}{N}\right)}^{{\alpha }_N}+{\left(\frac{S_c}{S_{\min }(S)}\right)}^{{\alpha }_S}$ 预测最优模型大小 $N$ 、最优批量大小 $B$ 、最优步骤数 $S$ 和数据集大小 $D$ 应按如下方式增长
     $$N\propto C_C^{{\alpha }_C^{\min }/{\alpha }_N},B\propto C^{{\alpha }_C^{\min }/{\alpha }_B},S\propto C_C^{{\alpha }_C^{\min }/{\alpha }_S},D=B?S$$ 其中
     $${\alpha }_C^{\min }=1/\left(1/{\alpha }_S+1/{\alpha }_B+1/{\alpha }_N\right)$$ 作者拟合的最优结果为 $N(C_{\min })\propto C_{\min }^{0.73},B_{\text{crit?}}\propto C_{\min }^{0.24},S_{\min }\propto C_{\min }^{0.03}$，这意味着随着计算量预算 $C$ 的提高，应该更多地增加模型参数量 $N$，较少地增加训练数据量 $D$

  8. 最优 batch size：使用合适的 batch size 进行训练可以实现最高的训练效率，关键 batch size 的大小 $B_{\text{crit}}$ 可以通过测量梯度噪声规模来确定，作者进一步验证了它仅和目标性能（损失值）有关，且呈现幂律关系，而与模型规模等其他因素无关

     

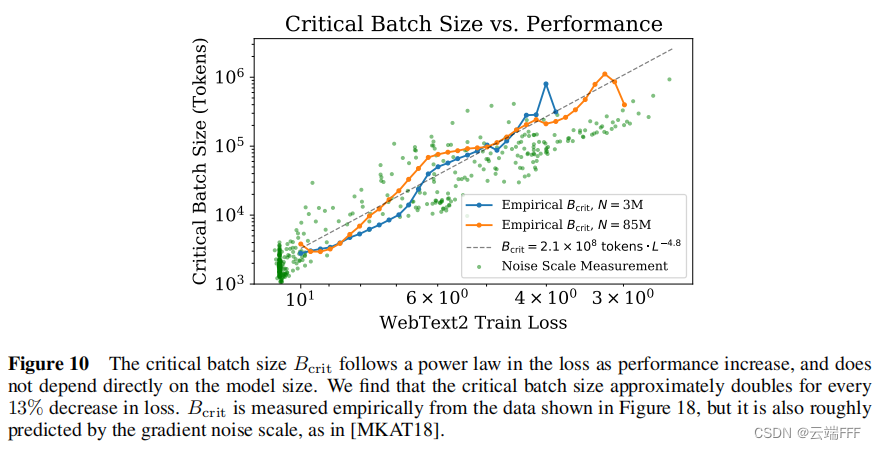
     最佳 batch size $B_{\text{crit?}}(L)$ 仅和性能 $L$ 相关，而与模型规模等其他因素无关。幂律关系表示为为
     $$B_{\text{crit?}}(L)\approx \frac{B_{?}}{L^{1/{\alpha }_B}}$$ 其中 $B_{?}$ 和 ${\alpha }_B$ 是需要拟合的参数，这种表示可以使 $B_{\text{crit?}}(L)$ 的估计值在 $L\to 0$ 时发散，以保持和另一种估计方法 “噪声梯度度量” 的一致性

• 最后，必须注意以上 Scaling Laws 都是针对 “最大化训练效率” 而言的。有时我们会故意违反它，比如 LLaMa 就使用更多的数据训练了较小的模型，虽然训练效率低，但是可以减少部署和推理成本