N皇后II（回溯算法）

2023-12-13 06:46:06

n?皇后问题 研究的是如何将 n?个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

要求：使用回溯算法设计程序

示例 1：

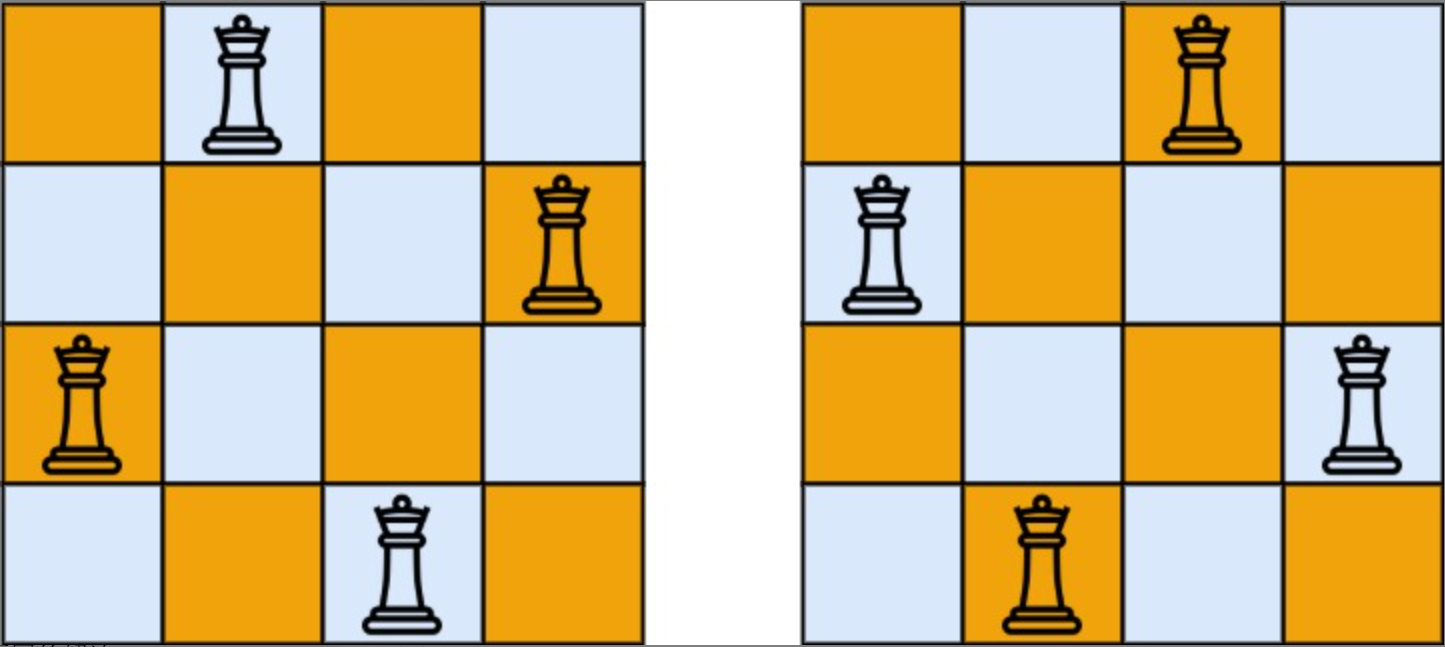
输入：

4

输出：

2

解释：如上图所示，4 皇后问题存在两个不同的解法。

输入：

1

输出：

1

def totalNQueens(n):
    columns = set()
    diagonal1 = set()
    diagonal2 = set()
    def backtrack(rowNum): 
        if rowNum == n:
            return 1
        else:
            count = 0
            for column in range(n):
                if column in columns or rowNum - column in diagonal1 or rowNum + column in diagonal2:
                    continue
                columns.add(column)
                diagonal1.add(rowNum - column)
                diagonal2.add(rowNum + column)
                count += backtrack(rowNum + 1)
                columns.remove(column)
                diagonal1.remove(rowNum - column)
                diagonal2.remove(rowNum + column)
            return count
    return backtrack(0)
n = eval(input())
print(totalNQueens(n))

文章来源:https://blog.csdn.net/m0_73811154/article/details/134844330
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。