C++算法之高精度计算

目录

高精度算法介绍

高精度算法应用

? ?高精度加法

? ?高精度减法

? ?高精度乘法

? ?高精度除法

? ??高精度除以低精度?

? ??高精度除以高精度

高精度算法介绍

? ? ? ?在C/C++中，我们经常会遇到限定数据范围的情况，我们先来看一下常用的int和long long两种数据类型的范围。

? ? ? ?C++标准规定：

? ? ? ?int占一个机器字长，在32位系统中int占32位，即4个字节，所以int的范围是[-,],为数量级。long long的范围则是[,],为数量级。如果超过该数量级，就需要用到高精度算法。

高精度算法应用

? ? 高精度加法

? ? ?1.输入两个整数a,b,输出它们的和(a,b<=）

? ? ? ?直接使用int/long long进行设变量计算。

? ? ? 2.输入两个整数a,b，输入它们的和(a,b<=）

? ? ? ?分析:int:~,数量级为，long long:~,数量级为，解决方案：用数组模拟高精度。

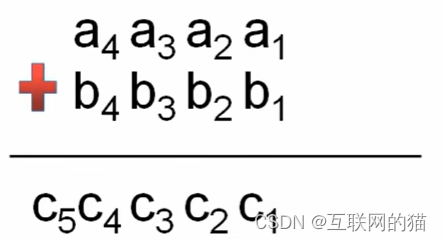算法核心：c[i]=a[i]+b[i],c[i+1]=c[i]/10,c[i]=c[i]%10;

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cstdlib>
using namespace std;
char s1[505],s2[505];//用数组模拟
int a[505],b[505],c[505];
int main(){
	int la,lb,lc;
	scanf("%s",s1);//输入两个整数，作为字符串输入
	scanf("%s",s2);
	la=strlen(s1);//计算对应的长度
	lb=strlen(s2);
	for(int i=0;i<la;i++){//将字符串转化为对应的数字，并且倒置过来，比如四位数加三位数，直接输入的话，无法对应位数加和
		a[la-i]=s1[i]-'0';
	}
	for(int i=0;i<lb;i++){
		b[lb-i]=s2[i]-'0';
	}
	lc=max(la,lb)+1;
	for(int i=1;i<=lc;i++){//高精度相加
		c[i]+=a[i]+b[i];
		c[i+1]=c[i]/10;
		c[i]=c[i]%10;
	}
	if(c[lc]==0&&lc>0){//去掉前导0，比如计算出来的210，其实是012，需要去掉0
		lc--;
	}
	for(int i=lc;i>0;i--){//输出计算结果
		printf("%d",c[i]);
	}
	return 0;
}

? ?高精度减法

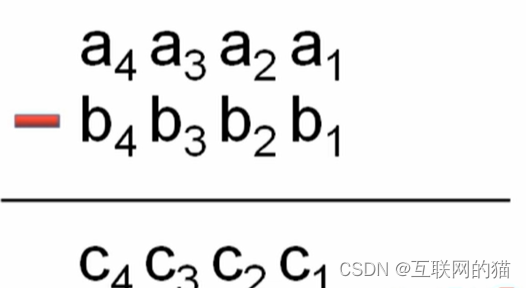要点：1.如果a<b，则需要交换a与b，最后计算完以后添加一个负号即可。2.如果a[i]<b[i]，需要高位借一当十使用。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cstdlib>
using namespace std;
char s1[10090],s2[10090],s3[10090];
int a[10090],b[10090],c[10090];
int flag=0;
bool compare(char s1[],char s2[]){//比较s1和s2大小
	int u=strlen(s1),v=strlen(s2);
	if(u!=v){
		return u>v;
	}
	for(int i=0;i<u;i++){
		if(s1[i]!=s2[i]){
			return s1[i]>s2[i];
		}
	}
	return true;
} 
int main(){
	int la,lb,lc;
	scanf("%s",s1);
	scanf("%s",s2);
	if(!compare(s1,s2)){//字符交换
		flag=1;//记录
		strcpy(s3,s1);
		strcpy(s1,s2);
		strcpy(s2,s3);
	}
	for(int i=0;i<la;i++){
		a[la-i]=s1[i]-'0';
	}
	for(int i=0;i<lb;i++){
		b[lb-i]=s2[i]-'0';
	}
	lc=max(la,lb);
	for(int i=1;i<=lc;i++){//高精度减法
		if(a[i]<b[i]){
			a[i+1]--;
			a[i]+=10;
		}
		c[i]=a[i]-b[i];
	}
	while(c[lc]==0&&lc>1){//去掉前导0
		lc--;
	}
	if(flag==1){//交换过的最后加上负号
		printf("-");
	}
	for(int i=lc;i>0;i--){
		printf("%d",c[i]);
	}
	return 0;
}

? ?高精度乘法

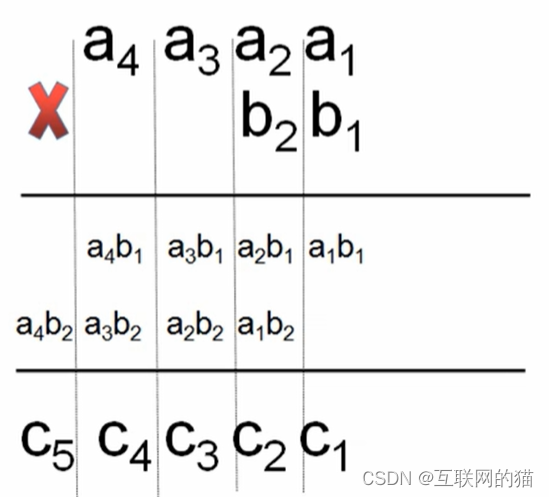? ? ? 通过图示分析，我们发现规律，a[1]*b[1]对应c[1]位置，a[2]*b[1]对应c[2]位置，a[3]*b[1]对应c[3]位置，a[4]*b[1]对应c[4]位置，a[1]*b[2]对应c[2]，a[2]*b[2]对应c[3]位置，a[3]*b[2]对应c[4]位置，a[4]*b[2]对应c[5]位置。

? ? ? 容易得出a[i]*b[j]对应c[i+j-1]位置，然后考虑进位，我们可以得到c[i+j-1]的关系式：c[i+j-1]+=a[i]*b[j];c[i+j]=c[i+j-1]/10;c[i+j-1]%=10;

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cstdlib>
using namespace std;
char s1[2005],s2[2005];
int a[2005],b[2005],c[2005];
int main(){
	int la,lb,lc;
	scanf("%s",s1);
	scanf("%s",s2);
	la=strlen(s1);
	lb=strlen(s2);
	for(int i=0;i<la;i++){
		a[la-i]=s1[i]-'0';
	}
	for(int i=0;i<lb;i++){
		b[lb-i]=s2[i]-'0';
	}
	lc=la+lb;
	for(int i=1;i<=la;i++){//高精度乘法
		for(int j=1;j<=lb;j++){
			c[i+j-1]=a[i]*b[j];
			c[i+j]=c[i+j-1]/10;
			c[i+j-1]%=10;
		}
	}
	if(c[lc]==0&&lc>0){
		lc--;
	}
	for(int i=lc;i>0;i--){
		printf("%d",c[i]);
	}
	return 0;
}

? ?高精度除法

? ??高精度除以低精度?

也就是大数除以小数，使用逐位试商法（也就是不断求商和求余数的过程）

#include<iostream>
#include<cstring>
using namespace std;
char s1[5005];//存储大数 
long long b,c[5005],x,a[5005],la,lc;//存储小数 
int main(){
	cin>>s1>>b;
	la=strlen(s1);//被除数的长度 
	for(int i=1;i<=la;i++){
		a[i]=s1[i-1]-'0';
	}
	for(int i=1;i<=la;++i){
		c[i]=(x*10+a[i])/b;//求商 
		x=(x*10+a[i])%10;//求余数 
	}
	lc=1;
	while(c[lc]==0&&lc<la){
		lc++;
	} 
	for(int i=lc;i<=la;i++){
		cout<<c[i];
	} 
	return 0;
}

? ? ?高精度除以高精度

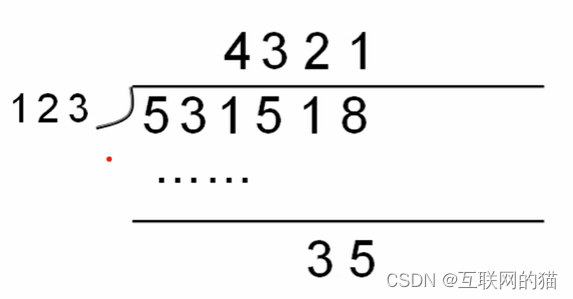方法：减法模拟除法

#include<iostream>
#include<cstring>
using namespace std;
char s1[305],s2[305];
int a[305],b[305],c[305],tmp[305];//a为被除数，b为除数,c为商
void init(int *x){
	char s[305];
	cin>>s;
	x[0]=strlen(s);
	for(int i=0;i<x[0];i++){
		x[x[0]-i]=s[i]-'0';//将字符串转化为数字，并且倒叙存储 
	}
} 
void print(int a[]){
	if(a[0]==0){
		cout<<0;
		return;
	}
	for(int i=a[0];i>0;i--){
		cout<<a[i];
	}
	return;
}
int compare(int a[],int b[]){//返回1表示a>b,返回0表示a=b，返回-1表示a<b 
 
	if(a[0]>b[0]){
		return 1;
	}
	if(a[0]<b[0]){
		return -1;
	}
	for(int i=a[0];i>0;i--){
		if(a[i]>b[i]){
			return 1;
		}
		if(a[i]<b[i]){
			return -1;
		}
	}
	return 0;
}
void minu(int a[],int b[]){
	for(int i=1;i<=a[0];i++){
		if(a[i]<b[i]){
			a[i+1]--;
			a[i]=a[i]+10;
		}
		a[i]=a[i]-b[i];
	}
	while(a[a[0]]==0&&a[0]>0){
		a[0]--;
	}//删除a的前导0，修正a的位数 
}
void numcpy(int p[],int q[],int n){//将除数移动相应的位数 
	for(int i=1;i<=p[0];i++){
		q[i+n-1]=p[i];
	}
	q[0]=p[0]+n-1;//移动后数组的位数 
}
int main(){
	init(a);//输入a 
	init(b);//输入b
	c[0]=a[0]-b[0]+1;
	for(int i=c[0];i>=1;i--){
		memset(tmp,0,sizeof(tmp));
		numcpy(b,tmp,i);//除数移动相应的位数 
		while(compare(a,tmp)>=0){//当被除数大于除数时执行循环 
			c[i]++;
			minu(a,tmp);
		}
	} 
	while(c[c[0]]==0&&c[0]>0){
		c[0]--;
	}
	print(c);//商 
	cout<<endl;
	print(a);//余数 
	return 0;
}