模型集成系列:投票分类器的原理和案例
模型集成系列:投票分类器的原理和案例

# 导入matplotlib库中的pyplot模块,并将其命名为plt
from matplotlib import pyplot as plt
# 导入seaborn库
import seaborn as sns
目录
- 1. 引言
- 2. 设置
- 3. 数据预处理
- 4. 模型选择
- 5. 使用硬投票的投票分类器
- 6. 使用软投票的投票分类器
- 7. 结果比较
- 8. 使用软投票的投票分类器的AUC-ROC曲线
- 9. 使用软投票的投票分类器的精确率-召回率曲线(PR曲线)
- 10. 我的其他笔记本
- 11. 参考文献
1. 介绍
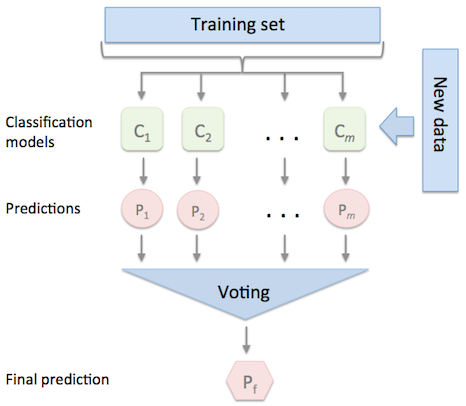
投票分类器是一种集成学习方法,它将多个基本模型组合起来产生最终的最优解。我们创建一个单一模型,通过这些模型进行训练,并根据它们对每个输出类别的投票多数来预测输出。
该算法将每个传入投票分类器的分类器的结果进行聚合,并根据最高的投票多数来预测输出类别。
由于投票依赖于许多模型的性能,它们不会受到一个模型的大误差或错误分类的影响。换句话说,一个模型的差性能可以被其他模型的强性能抵消。
1.1 硬投票 Hard Voting
硬投票(也称为多数投票)。模型独立地预测输出类别。输出类别是获得多数票的类别。
假设有三个分类器预测了输出类别(A,A,B),因此多数预测为A。因此,A将成为最终的预测结果。
1.2 加权多数投票 Weighted Majority Voting
此外,除了前一节中描述的简单多数投票(硬投票)外,我们还可以通过将权重w与分类器C关联来计算加权多数投票。
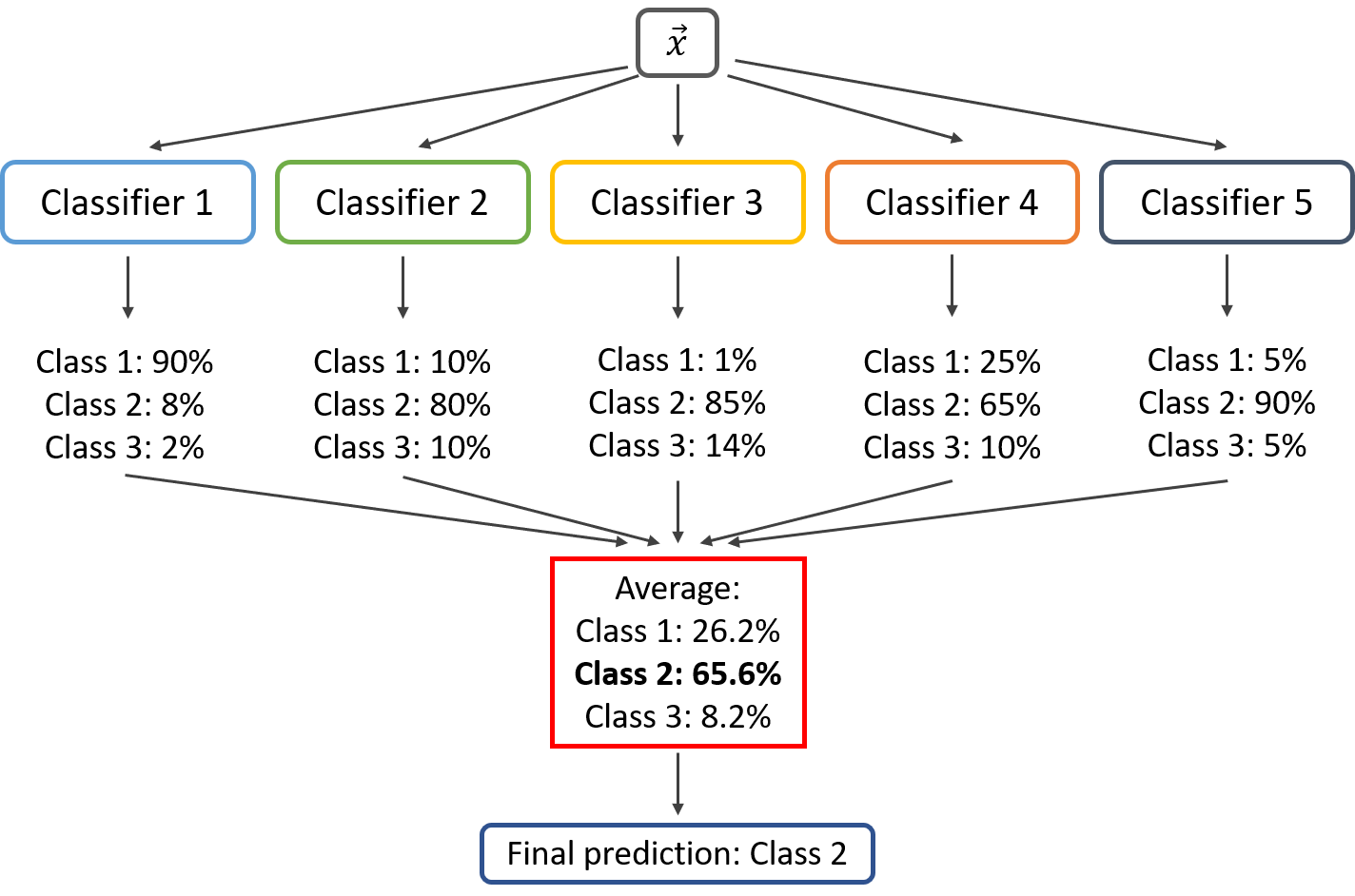
1.3 软投票
软投票是一种集成学习方法,它通过组合多个不同的分类器的预测结果来进行最终的决策。每个分类器都会对样本进行预测,并给出一个类别的概率分布。软投票会将所有分类器的预测结果加权平均,然后选择具有最高概率的类别作为最终的预测结果。
软投票的优点是可以利用多个分类器的优势,从而提高整体的预测准确率。它适用于各种不同的分类器,包括决策树、支持向量机、逻辑回归等。
软投票的步骤如下:
- 对于每个分类器,对样本进行预测,并得到一个类别的概率分布。
- 将所有分类器的预测结果加权平均,得到一个最终的概率分布。
- 选择具有最高概率的类别作为最终的预测结果。
软投票的公式如下:
P
(
y
=
c
)
=
1
N
∑
i
=
1
N
P
i
(
y
=
c
)
P(y=c) = \frac{1}{N} \sum_{i=1}^{N} P_i(y=c)
P(y=c)=N1?i=1∑N?Pi?(y=c)
其中,
P
(
y
=
c
)
P(y=c)
P(y=c)表示类别
c
c
c的概率,
N
N
N表示分类器的数量,
P
i
(
y
=
c
)
P_i(y=c)
Pi?(y=c)表示分类器
i
i
i对类别
c
c
c的概率预测结果。
在软投票中,输出类别是基于给定类别的概率的平均预测。软投票是将每个模型中每个预测的概率相结合,并选择具有最高总概率的预测。
每个基本模型分类器独立地分配每种类型的发生概率。最后,计算每个类别的可能性的平均值,并且最终输出是具有最高概率的类别。
假设给定某个输入到三个模型,类别A的预测概率为(0.30, 0.47, 0.53),类别B的预测概率为(0.20, 0.32, 0.40)。所以类别A的平均值为0.4333,类别B的平均值为0.3067,显然,类别A是赢家,因为它的概率是由每个分类器平均计算得到的最高概率。
2. 设置
2.1 导入工具包
# 导入所需的库
import numpy as np
import pandas as pd
import seaborn as sns
import plotly.express as px
from matplotlib import pyplot as plt
from sklearn.model_selection import cross_val_score
from collections import Counter
2.2 Importing Data
# 尝试从指定路径读取心脏病预测数据集的csv文件
try:
raw_df = pd.read_csv('../input/heart-failure-prediction/heart.csv')
# 如果指定路径读取失败,则从当前路径读取
except:
raw_df = pd.read_csv('heart.csv')
2.3 心血管疾病数据集
心血管疾病(CVDs)是全球第一大死因,每年夺去约1790万人的生命,占全球所有死亡人数的31%。其中四分之三的CVD死亡是由心脏病和中风引起的,其中三分之一的死亡发生在70岁以下的人群中。心力衰竭是由CVD引起的常见事件,该数据集包含11个特征,可用于预测可能的心脏疾病。
患有心血管疾病或处于高心血管风险(由于存在一种或多种风险因素,如高血压,糖尿病,高脂血症或已经确诊的疾病)的人需要早期检测和管理,其中机器学习模型可以提供很大的帮助。
数据集中没有重复项和缺失值。
https://www.kaggle.com/datasets/fedesoriano/heart-failure-prediction
2.4 数据集属性
- 年龄:患者年龄[岁]
- 性别:患者性别[M: 男性, F: 女性]
- 胸痛类型:胸痛类型[TA: 典型心绞痛, ATA: 非典型心绞痛, NAP: 非心绞痛性疼痛, ASY: 无症状]- 静息血压:静息血压[mm Hg]
- 胆固醇:血清胆固醇[mm/dl]
- 空腹血糖:空腹血糖[1: 如果空腹血糖 > 120 mg/dl, 0: 否则]
- 静息心电图结果:静息心电图结果[正常: 正常, ST: ST-T波异常(T波倒置和/或ST段抬高或压低> 0.05 mV), LVH: 根据Estes标准显示可能或明确的左室肥厚]
- 最大心率:达到的最大心率[60到202之间的数值]
- 运动诱发心绞痛:运动诱发心绞痛[Y: 是, N: 否]
- ST下降:ST下降 = ST [以压低为单位的数值]
- ST段斜率:峰值运动ST段的斜率[上升: 上升, 平坦: 平坦, 下降: 下降]
- 心脏疾病:输出类别[1: 心脏疾病, 0: 正常]
# 显示数据的前几行
raw_df.head()
| Age | Sex | ChestPainType | RestingBP | Cholesterol | FastingBS | RestingECG | MaxHR | ExerciseAngina | Oldpeak | ST_Slope | HeartDisease | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 40 | M | ATA | 140 | 289 | 0 | Normal | 172 | N | 0.0 | Up | 0 |
| 1 | 49 | F | NAP | 160 | 180 | 0 | Normal | 156 | N | 1.0 | Flat | 1 |
| 2 | 37 | M | ATA | 130 | 283 | 0 | ST | 98 | N | 0.0 | Up | 0 |
| 3 | 48 | F | ASY | 138 | 214 | 0 | Normal | 108 | Y | 1.5 | Flat | 1 |
| 4 | 54 | M | NAP | 150 | 195 | 0 | Normal | 122 | N | 0.0 | Up | 0 |
3. 数据预处理
3.1 数据不平衡检查
# 给饼图添加中文注释
# 定义标签,分别表示"健康"和"心脏疾病"
labels = ["健康", "心脏疾病"]
# 统计心脏疾病的数量,返回一个列表
healthy_or_not = raw_df['HeartDisease'].value_counts().tolist()
# 将统计结果存储在一个列表中,分别表示"健康"和"心脏疾病"的数量
values = [healthy_or_not[0], healthy_or_not[1]]
# 创建一个饼图对象,设置参数:数值、标签、宽度、高度、颜色序列和标题
fig = px.pie(values=raw_df['HeartDisease'].value_counts(), names=labels, width=700, height=400, color_discrete_sequence=["skyblue", "black"], title="健康 vs 心脏疾病")
# 显示饼图
fig.show()
var gd = document.getElementById(‘192dfa40-8f7a-4996-a296-b8adb0e266cc’);
var x = new MutationObserver(function (mutations, observer) {{
var display = window.getComputedStyle(gd).display;
if (!display || display === ‘none’) {{
console.log([gd, ‘removed!’]);
Plotly.purge(gd);
observer.disconnect();
}}
}});
// Listen for the removal of the full notebook cells
var notebookContainer = gd.closest(‘#notebook-container’);
if (notebookContainer) {{
x.observe(notebookContainer, {childList: true});
}}
// Listen for the clearing of the current output cell
var outputEl = gd.closest(‘.output’);
if (outputEl) {{
x.observe(outputEl, {childList: true});
}}
}) }; }); </script> </div>
我们可以看到数据相当平衡,所以我们不需要利用欠采样或过采样技术。
3.2 检查异常值
# 创建一个包含数值型特征的列表
numerical_columns = list(raw_df.loc[:,['Age', 'RestingBP', 'Cholesterol', 'MaxHR', 'Oldpeak']])
# 创建一个包含分类特征的列表
categorical_columns = list(raw_df.loc[:,['Sex', 'ChestPainType', 'FastingBS', 'RestingECG', 'ExerciseAngina', 'ST_Slope']])
# 定义一个函数,用于绘制自定义的箱线图
def boxplots_custom(dataset, columns_list, rows, cols, suptitle):
# 创建一个包含多个子图的图形对象
fig, axs = plt.subplots(rows, cols, sharey=True, figsize=(13,5))
# 设置总标题
fig.suptitle(suptitle,y=1, size=25)
# 将子图展平为一维数组
axs = axs.flatten()
# 遍历列名列表,绘制每个变量的箱线图
for i, data in enumerate(columns_list):
# 绘制箱线图
sns.boxplot(data=dataset[data], orient='h', ax=axs[i])
# 设置子图标题,包括变量名和偏度值
axs[i].set_title(data + ', skewness is: '+str(round(dataset[data].skew(axis = 0, skipna = True),2)))
# 调用函数绘制箱线图
boxplots_custom(dataset=raw_df, columns_list=numerical_columns, rows=2, cols=3, suptitle='Boxplots for each variable')
# 调整子图的布局
plt.tight_layout()

3.3 四分位距 (IQR)
Tukey’s (1977) 方法用于检测偏斜或非钟形数据中的异常值,因为它不做分布假设。然而,Tukey的方法可能不适用于小样本量。一般规则是,不在(Q1-1.5 IQR)和(Q3+1.5 IQR)范围内的任何值都是异常值,可以被删除。
四分位距(IQR)是最广泛用于异常值检测和删除的方法之一。
过程:
- 找到第一四分位数Q1。
- 找到第三四分位数Q3。
- 计算IQR。IQR = Q3-Q1。
- 用下限Q1-1.5 IQR和上限Q3+1.5 IQR定义正常数据范围。
# 定义一个函数IQR_method,用于检测数据集中的异常值
# 参数:
# - df: 数据集,类型为DataFrame
# - n: 异常值的阈值,类型为整数
# - features: 需要检测异常值的特征列表,类型为列表
def IQR_method(df, n, features):
# 创建一个空列表,用于存储异常值的索引
outlier_list = []
# 遍历特征列表中的每个特征
for column in features:
# 计算第一四分位数(25%)
Q1 = np.percentile(df[column], 25)
# 计算第三四分位数(75%)
Q3 = np.percentile(df[column], 75)
# 计算四分位距(IQR)
IQR = Q3 - Q1
# 计算异常值的阈值
outlier_step = 1.5 * IQR
# 确定异常值的索引列表
outlier_list_column = df[(df[column] < Q1 - outlier_step) | (df[column] > Q3 + outlier_step)].index
# 将异常值的索引列表添加到总的异常值列表中
outlier_list.extend(outlier_list_column)
# 统计每个索引出现的次数
outlier_list = Counter(outlier_list)
# 选取出现次数大于阈值n的索引
multiple_outliers = list(k for k, v in outlier_list.items() if v > n)
# 计算低于和高于边界值的记录数
out1 = df[df[column] < Q1 - outlier_step]
out2 = df[df[column] > Q3 + outlier_step]
# 打印删除的异常值总数
print('Total number of deleted outliers is:', out1.shape[0] + out2.shape[0])
# 返回多个异常值的索引列表
return multiple_outliers
3.4 删除异常值
# 检测异常值
Outliers_IQR = IQR_method(raw_df,1,numerical_columns)
# 删除异常值
df = raw_df.drop(Outliers_IQR, axis = 0).reset_index(drop=True)
Total number of deleted outliers is: 16
3.5 创建虚拟变量
# 使用pd.get_dummies()函数对数据框df进行独热编码处理,并且将原始的列删除
# drop_first=True表示删除每个分类变量的第一个类别,以避免多重共线性问题
df = pd.get_dummies(df, drop_first=True)
3.6 训练测试分割
# 从DataFrame中删除'HeartDisease'列,得到特征矩阵X
X = df.drop('HeartDisease', axis=1)
# 从DataFrame中提取'HeartDisease'列,得到目标变量y
y = df['HeartDisease']
# 导入train_test_split函数用于划分训练集和测试集
from sklearn.model_selection import train_test_split
# 使用train_test_split函数划分数据集
# 参数X表示特征数据集,y表示目标数据集
# 参数stratify=y表示按照目标数据集y的类别比例进行划分,保证训练集和测试集中各类别样本的比例相同
# 参数test_size=0.3表示将数据集划分为训练集和测试集的比例为70%:30%
# 参数random_state=42表示设置随机种子,保证每次划分的结果相同
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.3, random_state=42)
3.7 特征缩放
# 导入StandardScaler类
from sklearn.preprocessing import StandardScaler
# 创建一个函数用于特征缩放
def Standard_Scaler(df, col_names):
# 从数据框中选择需要缩放的特征列
features = df[col_names]
# 创建一个StandardScaler对象,并使用特征列的值进行拟合
scaler = StandardScaler().fit(features.values)
# 使用拟合后的scaler对象对特征列进行缩放
features = scaler.transform(features.values)
# 将缩放后的特征列更新到原始数据框中
df[col_names] = features
# 返回更新后的数据框
return df
col_names = numerical_columns
# 将训练集数据进行标准化处理
X_train = Standard_Scaler(X_train, col_names)
# 将测试集数据进行标准化处理
X_test = Standard_Scaler(X_test, col_names)
4.模型选择
# 导入所需的库和模型
from sklearn.ensemble import VotingClassifier # 导入投票分类器
from sklearn.ensemble import RandomForestClassifier # 导入随机森林分类器
from sklearn.neighbors import KNeighborsClassifier # 导入K近邻分类器
from sklearn.svm import SVC # 导入支持向量机分类器
from sklearn.neural_network import MLPClassifier # 导入多层感知机分类器
from sklearn.ensemble import AdaBoostClassifier # 导入AdaBoost分类器
from sklearn.ensemble import GradientBoostingClassifier # 导入梯度提升分类器
from sklearn.ensemble import ExtraTreesClassifier # 导入极端随机树分类器
from sklearn.linear_model import LogisticRegression # 导入逻辑回归分类器
from xgboost import XGBClassifier # 导入XGBoost分类器
from catboost import CatBoostClassifier # 导入CatBoost分类器
# 导入所需的库
from sklearn.metrics import confusion_matrix, recall_score, precision_score, f1_score, accuracy_score
from sklearn.metrics import classification_report
# 将Neural Network分类器模型添加到estimator列表中,使用MLPClassifier作为分类器,设置最大迭代次数为10000
# 将LogisticRegression分类器模型添加到estimator列表中,使用LogisticRegression作为分类器,设置求解器为'lbfgs',多分类为'multinomial',最大迭代次数为200
# 将ExtraTreesClassifier分类器模型添加到estimator列表中,使用ExtraTreesClassifier作为分类器
# 将RandomForest分类器模型添加到estimator列表中,使用RandomForestClassifier作为分类器
# 将SVC分类器模型添加到estimator列表中,使用SVC作为分类器,设置gamma为'auto',启用概率估计
# 将AdaBoostClassifier分类器模型添加到estimator列表中,使用AdaBoostClassifier作为分类器
# 将GradientBoostingClassifier分类器模型添加到estimator列表中,使用GradientBoostingClassifier作为分类器
# 将XGB分类器模型添加到estimator列表中,使用XGBClassifier作为分类器
# 将CatBoost分类器模型添加到estimator列表中,使用CatBoostClassifier作为分类器,设置日志级别为'Silent'
estimator = []
estimator.append(('Neural Network', MLPClassifier(max_iter = 10000) ))
estimator.append(('LogisticRegression', LogisticRegression(solver ='lbfgs', multi_class ='multinomial', max_iter = 200)))
estimator.append(('ExtraTreesClassifier', ExtraTreesClassifier() ))
estimator.append(('RandomForest', RandomForestClassifier() ))
#estimator.append(('KNN', KNeighborsClassifier() ))
estimator.append(('SVC', SVC(gamma ='auto', probability = True)))
estimator.append(('AdaBoostClassifier', AdaBoostClassifier() ))
estimator.append(('GradientBoostingClassifier', GradientBoostingClassifier() ))
estimator.append(('XGB', XGBClassifier() ))
estimator.append(('CatBoost', CatBoostClassifier(logging_level='Silent') ))
5. 带有硬投票的投票分类器
# 创建一个 VotingClassifier 对象,使用 hard voting 策略
VC_hard = VotingClassifier(estimators = estimator, voting ='hard')
# 使用训练集数据进行模型训练
VC_hard.fit(X_train, y_train)
# 使用训练好的模型对测试集数据进行预测
y_pred = VC_hard.predict(X_test)
5.1 分类报告
# 输出分类报告
print(classification_report(y_test, y_pred))
precision recall f1-score support
0 0.90 0.87 0.88 122
1 0.90 0.92 0.91 150
accuracy 0.90 272
macro avg 0.90 0.89 0.90 272
weighted avg 0.90 0.90 0.90 272
5.2 混淆矩阵
# 计算混淆矩阵
cm = confusion_matrix(y_test, y_pred)
# 计算召回率
VC_hard_Recall = recall_score(y_test, y_pred)
# 计算精确率
VC_hard_Precision = precision_score(y_test, y_pred)
# 计算F1值
VC_hard_f1 = f1_score(y_test, y_pred)
# 计算准确率
VC_hard_accuracy = accuracy_score(y_test, y_pred)
# 打印混淆矩阵
print(cm)
[[106 16]
[ 12 138]]
5.3 K-Fold 交叉验证
交叉验证是一种重采样过程,用于评估机器学习模型在有限数据样本上的表现。该过程有一个称为k的单一参数,它指的是给定数据样本要被分成的组数。因此,该过程通常被称为k折交叉验证。
交叉验证的目的是测试机器学习模型预测新数据的能力。
# 导入statistics模块中的stdev函数
from statistics import stdev
# 使用cross_val_score函数对模型进行交叉验证,计算模型在每个折叠数据上的召回率得分
score = cross_val_score(VC_hard, X_train, y_train, cv=5, scoring='recall')
# 计算交叉验证召回率得分的平均值
VC_hard_cv_score = score.mean()
# 计算交叉验证召回率得分的标准差
VC_hard_cv_stdev = stdev(score)
# 打印交叉验证召回率得分
print('Cross Validation Recall scores are: {}'.format(score))
# 打印平均交叉验证召回率得分
print('Average Cross Validation Recall score: ', VC_hard_cv_score)
# 打印交叉验证召回率得分的标准差
print('Cross Validation Recall standard deviation: ', VC_hard_cv_stdev)
Cross Validation Recall scores are: [0.92857143 0.84285714 0.85714286 0.92753623 0.89855072]
Average Cross Validation Recall score: 0.8909316770186336
Cross Validation Recall standard deviation: 0.039583896359237175
# 创建一个包含VC_hard_Recall, VC_hard_Precision, VC_hard_f1, VC_hard_accuracy, VC_hard_cv_score, VC_hard_cv_stdev的元组ndf
ndf = [(VC_hard_Recall, VC_hard_Precision, VC_hard_f1, VC_hard_accuracy, VC_hard_cv_score, VC_hard_cv_stdev)]
# 使用pandas库的DataFrame函数将ndf转换为数据框VC_hard_score,并指定列名
VC_hard_score = pd.DataFrame(data = ndf, columns=['Recall','Precision','F1 Score', 'Accuracy', 'Avg CV Recall', 'Standard Deviation of CV Recall'])
# 在VC_hard_score数据框中插入一列名为'Voting Classifier',值为'Hard Voting'的列
VC_hard_score.insert(0, 'Voting Classifier', 'Hard Voting')
# 返回VC_hard_score数据框
| Voting Classifier | Recall | Precision | F1 Score | Accuracy | Avg CV Recall | Standard Deviation of CV Recall | |
|---|---|---|---|---|---|---|---|
| 0 | Hard Voting | 0.92 | 0.896104 | 0.907895 | 0.897059 | 0.890932 | 0.039584 |
6. 6. 使用软投票的投票分类器
# 创建一个VotingClassifier对象,使用soft voting策略
VC_soft = VotingClassifier(estimators = estimator, voting ='soft')
# 使用训练集X_train和y_train来训练VotingClassifier模型
VC_soft.fit(X_train, y_train)
# 使用训练好的模型对测试集X_test进行预测
y_pred = VC_soft.predict(X_test)
6.1分类报告
# 导入classification_report函数
from sklearn.metrics import classification_report
# 打印分类报告,比较预测结果和真实结果的差异
print(classification_report(y_test, y_pred))
precision recall f1-score support
0 0.90 0.89 0.90 122
1 0.91 0.92 0.92 150
accuracy 0.91 272
macro avg 0.91 0.91 0.91 272
weighted avg 0.91 0.91 0.91 272
6.2 混淆矩阵
# 计算混淆矩阵
cm = confusion_matrix(y_test, y_pred)
# 计算召回率
VC_soft_Recall = recall_score(y_test, y_pred)
# 计算精确率
VC_soft_Precision = precision_score(y_test, y_pred)
# 计算F1分数
VC_soft_f1 = f1_score(y_test, y_pred)
# 计算准确率
VC_soft_accuracy = accuracy_score(y_test, y_pred)
# 打印混淆矩阵
print(cm)
[[109 13]
[ 12 138]]
6.3 K-Fold交叉验证
# 使用交叉验证计算模型的召回率得分
# 参数说明:
# - VC_soft: 使用的分类器模型
# - X_train: 训练数据集的特征矩阵
# - y_train: 训练数据集的标签
# - cv=5: 交叉验证的折数,这里使用5折交叉验证
# - scoring='recall': 使用召回率作为评估指标
score2 = cross_val_score(VC_soft, X_train, y_train, cv=5, scoring='recall')
# 计算交叉验证的平均召回率分数
VC_soft_cv_score = score2.mean()
# 计算交叉验证召回率分数的标准差
VC_soft_cv_stdev = stdev(score2)
# 打印交叉验证的召回率分数
print('Cross Validation Recall scores are: {}'.format(score2))
# 打印平均交叉验证召回率分数
print('Average Cross Validation Recall score: ', VC_soft_cv_score)
# 打印交叉验证召回率分数的标准差
print('Cross Validation Recall standard deviation: ', VC_soft_cv_stdev)
Cross Validation Recall scores are: [0.91428571 0.84285714 0.82857143 0.89855072 0.89855072]
Average Cross Validation Recall score: 0.8765631469979297
Cross Validation Recall standard deviation: 0.0381745955328178
# 给数据框添加中文注释
# 创建一个包含评分指标的数据框ndf2
ndf2 = [(VC_soft_Recall, VC_soft_Precision, VC_soft_f1, VC_soft_accuracy, VC_soft_cv_score, VC_soft_cv_stdev)]
# 使用ndf2数据创建一个数据框VC_soft_score,并指定列名
VC_soft_score = pd.DataFrame(data = ndf2, columns=['Recall','Precision','F1 Score', 'Accuracy', 'Avg CV Recall', 'Standard Deviation of CV Recall'])
# 在VC_soft_score数据框中插入一列,列名为'Voting Classifier',值为'Soft Voting'
VC_soft_score.insert(0, 'Voting Classifier', 'Soft Voting')
# 返回VC_soft_score数据框
| Voting Classifier | Recall | Precision | F1 Score | Accuracy | Avg CV Recall | Standard Deviation of CV Recall | |
|---|---|---|---|---|---|---|---|
| 0 | Soft Voting | 0.92 | 0.913907 | 0.916944 | 0.908088 | 0.876563 | 0.038175 |
7. 结果比较
# 将VC_hard_score和VC_soft_score合并为一个DataFrame
predictions = pd.concat([VC_hard_score, VC_soft_score], ignore_index=True, sort=False)
# 按照'Avg CV Recall'列的值进行降序排序
predictions.sort_values(by=['Avg CV Recall'], ascending=False)
| Voting Classifier | Recall | Precision | F1 Score | Accuracy | Avg CV Recall | Standard Deviation of CV Recall | |
|---|---|---|---|---|---|---|---|
| 0 | Hard Voting | 0.92 | 0.896104 | 0.907895 | 0.897059 | 0.890932 | 0.039584 |
| 1 | Soft Voting | 0.92 | 0.913907 | 0.916944 | 0.908088 | 0.876563 | 0.038175 |
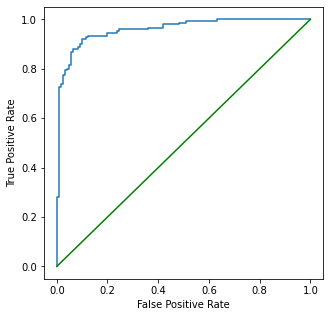
8. 使用软投票的投票分类器的AUC-ROC曲线
我使用软投票展示了一个投票分类器的AUC-ROC曲线,因为当voting='hard’时,predict_proba不可用。我使用软投票展示了一个投票分类器的AUC-ROC曲线,因为当voting='hard’时,predict_proba不可用。
# 导入roc_auc_score函数
from sklearn.metrics import roc_auc_score
# 使用roc_auc_score函数计算y_test和y_pred之间的ROC AUC得分
ROCAUCscore = roc_auc_score(y_test, y_pred)
# 打印带有ROC AUC得分的AUC-ROC曲线,使用了Voting Classifier和soft voting
print(f"AUC-ROC曲线(使用Voting Classifier和soft voting)的得分为:{ROCAUCscore:.4f}")
AUC-ROC Curve for Voting Classifier with soft voting: 0.9067
y_proba = VC_soft.predict_proba(X_test)
from sklearn.metrics import roc_curve
from sklearn.metrics import RocCurveDisplay
# 定义一个函数,用于绘制AUC-ROC曲线
def plot_auc_roc_curve(y_test, y_pred):
# 计算真正率(True Positive Rate)和假正率(False Positive Rate)
fpr, tpr, _ = roc_curve(y_test, y_pred)
# 创建一个ROC曲线的显示对象
roc_display = RocCurveDisplay(fpr=fpr, tpr=tpr).plot()
# 设置图像的大小为5x5
roc_display.figure_.set_size_inches(5,5)
# 绘制对角线,表示随机分类器的ROC曲线
plt.plot([0, 1], [0, 1], color = 'g')
# 使用sklearn方法绘制AUC-ROC曲线 - 好的绘图
plot_auc_roc_curve(y_test, y_proba[:, 1])
# 使用sklearn方法绘制AUC-ROC曲线 - 不好的绘图
#plot_sklearn_roc_curve(y_test, y_pred)
9. 使用软投票的投票分类器的精确率-召回率曲线
精确率-召回率曲线展示了在不同阈值下精确率和召回率之间的权衡关系。
# 导入需要的库
from sklearn.metrics import precision_recall_curve # 导入precision_recall_curve函数,用于计算精确率和召回率
from sklearn.metrics import PrecisionRecallDisplay # 导入PrecisionRecallDisplay类,用于显示精确率和召回率的曲线
# 使用PrecisionRecallDisplay类的from_estimator方法创建一个PrecisionRecallDisplay对象display
# 参数VC_soft表示使用的分类器模型
# 参数X_test表示测试集的特征数据
# 参数y_test表示测试集的标签数据
# 参数name表示显示曲线的名称
display = PrecisionRecallDisplay.from_estimator(VC_soft, X_test, y_test, name="Average precision")
# 设置显示图表的标题为"Voting Classifier with soft voting"
_ = display.ax_.set_title("Voting Classifier with soft voting")
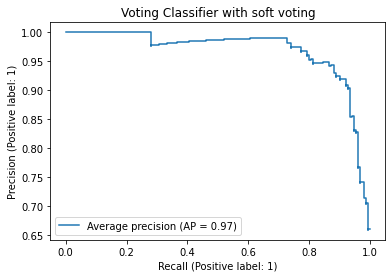
我们可以清楚地看到,为了获得更好的召回率,我们需要牺牲很多精确度。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!