DDPM之前向扩散
2024-01-09 17:01:11
一、理论
- 前向过程是一个逐渐加噪声的过程
- 噪声随时间变换,时间 t 越大,噪声越大
- 噪声服从正态分布
- 前向过程可以用条件概率
来描述?
?是在时间步 t 的数据状态
是在时间步 t?1 的数据状态
代表了在已知
的情况下,时间步 t 的数据状态
的概率分布
是一个高斯分布,
- 高斯分布
- 均值(Mean): 由
?给出
- 方差(Variance): 由
给出
- 均值(Mean): 由
二、可视化展示
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 假设的参数
beta_t = 0.1 # 假设的噪声方差
x_t_minus_1 = 0 # 假设在 t-1 时间步的 x 的值
mean = np.sqrt(1 - beta_t) * x_t_minus_1 # 高斯分布的均值
variance = beta_t # 高斯分布的方差
std_dev = np.sqrt(variance) # 标准差
# 创建 x 轴的数值
x = np.linspace(mean - 3*std_dev, mean + 3*std_dev, 100)
# 创建高斯分布的概率密度函数 (PDF)
pdf = norm.pdf(x, mean, std_dev)
# 绘制图像
plt.figure(figsize=(8, 4))
plt.plot(x, pdf, color='blue')
plt.title("Gaussian Distribution of $q(x_t | x_{t-1})$")
plt.xlabel("$x_t$")
plt.ylabel("Probability Density")
plt.grid(True)
plt.show()
?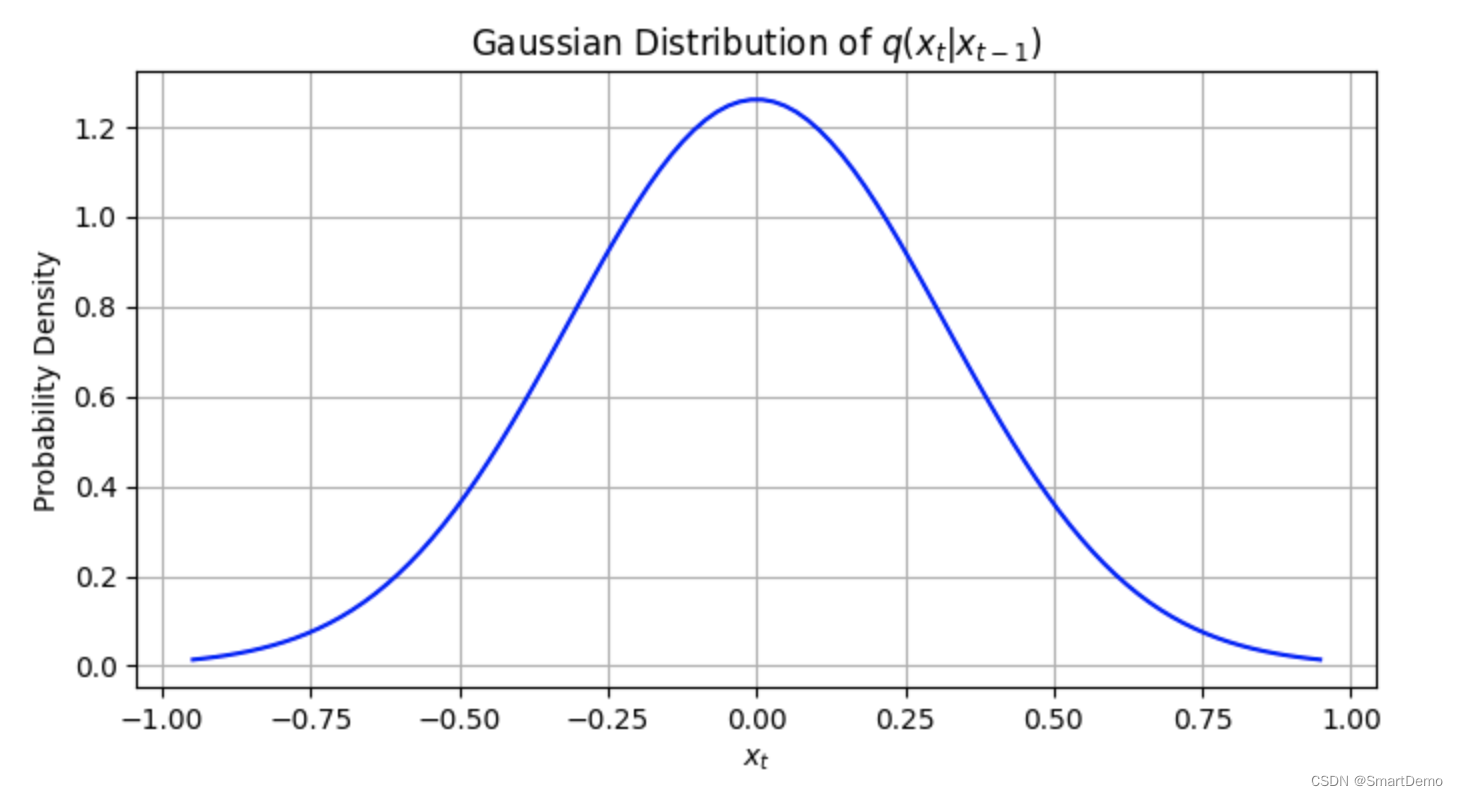
解释:
- 分布的均值将围绕
的缩放版本居中
- 这表示大多数数据点预期出现的平均值
- 这种缩放是通过
实现的
- 其中
是时间步
?的噪声方差
- 其中
- 曲线的宽度代表分布的方差,在本例中为
- 更大的
将导致更宽的曲线,表示由于更高的噪声水平而导致的数据更广泛的分布。
- 更大的
- 图形的x轴将表示
?的可能值,y轴将表示概率密度。
- 图形的标题将是“扩散步骤
”
- 表明它是在可视化扩散步骤中给定
的
的分布。
- 表明它是在可视化扩散步骤中给定
三、遗留问题?
至于均值和方差如何计算,这个涉及数学原理介绍,为方便鸟瞰式的理解,此处先不做展开。。
文章来源:https://blog.csdn.net/SmartDemo/article/details/135480737
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!