数据结构与算法要点总结（5）：树、二叉树、森林、堆、Huffman树

目录

1、树的基本术语

2、二叉树

常用性质：

?二叉树的二叉链表表示（最为常用）

二叉树的遍历：?

层序遍历

3、线索化二叉树

目的

练习题思路：

一道练习：

4、树与森林

仅介绍左子女右兄弟表示法

树的遍历：

森林与二叉树的转换

5、堆?

堆的建立：

下滑调整算法

?最小堆的插入

上浮调整

最小堆的删除

6、Huffman树

路径长度概念：

?完全二叉树的优势：

带权路径长度

?Huffman树

Huffman编码

---

1、树的基本术语

子女、双亲、兄弟、

度：结点的子女个数即为该结点的度；树中各个结点的度的最大值称为树的度。

结点的层次：规定根结点在第一层，其子女结点的层次等于它的层次加一。以下类推。

深度：结点的深度即为结点的层次；离根最远结点的层次即为树的深度。（从上往下标）

高度：规定叶结点的高度为1，其双亲结点的高度等于它的高度加一。 （从下往上标）

树的高度：等于根结点的高度，即根结点所有子女高度的最大值加一。

2、二叉树

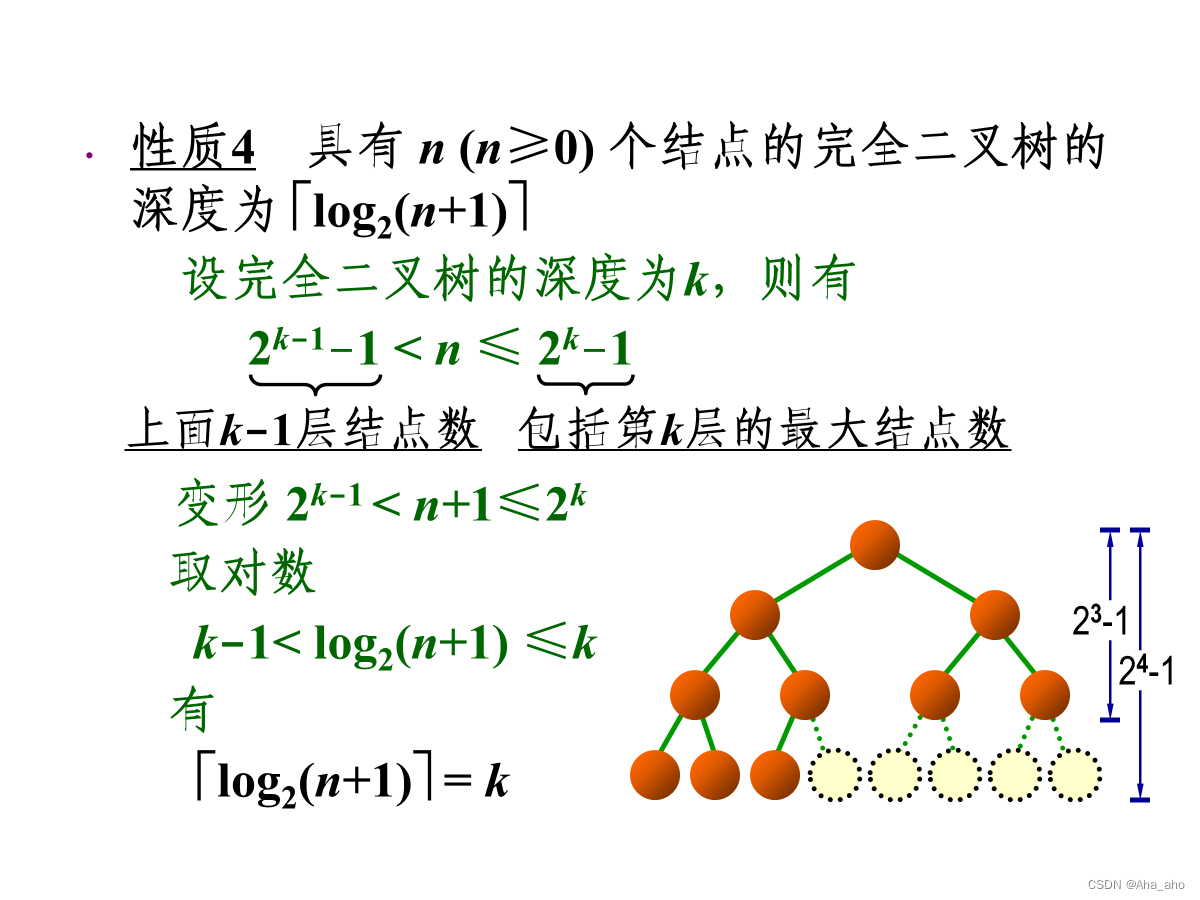
常用性质：

性质三中最重要的一点就是点数等于边数加一。?

注意：不同教材满二叉树和完全二叉树可能不同。

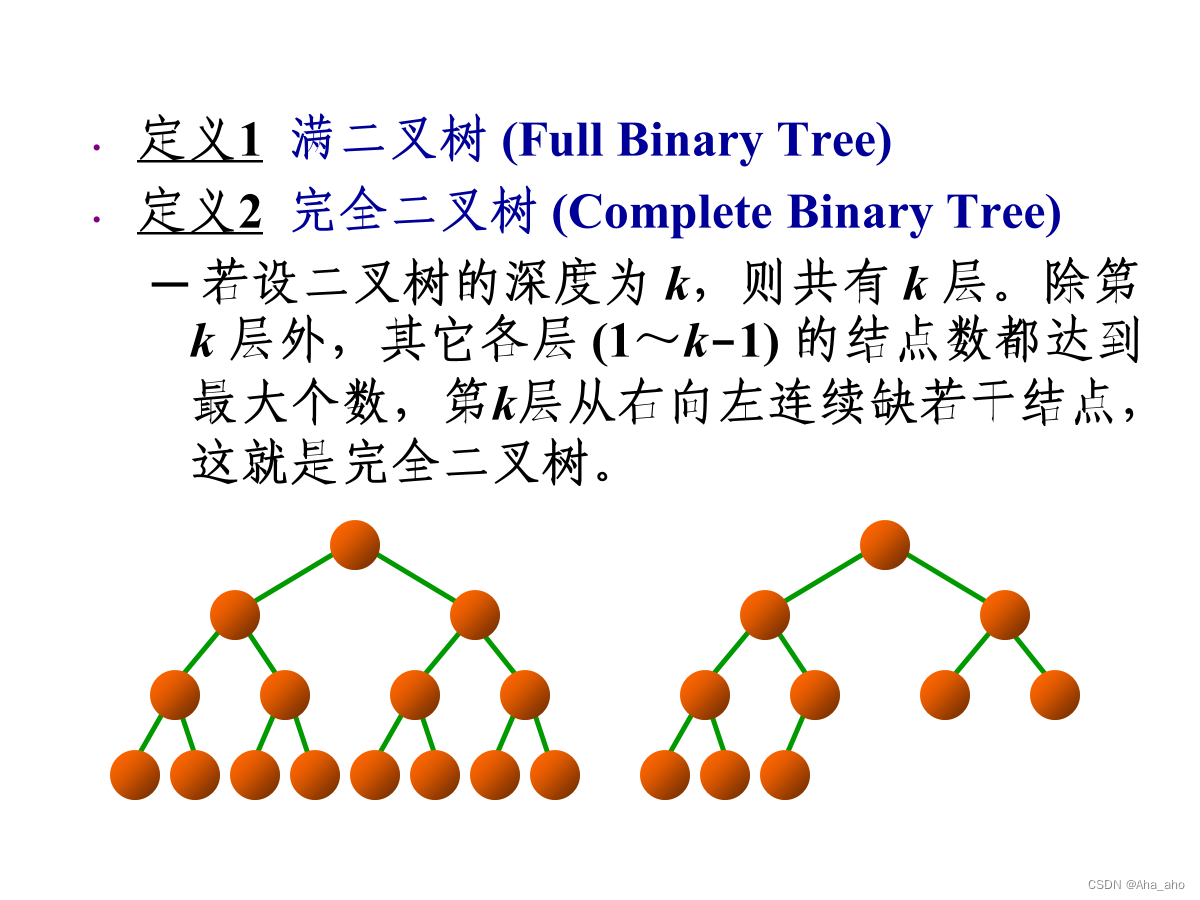
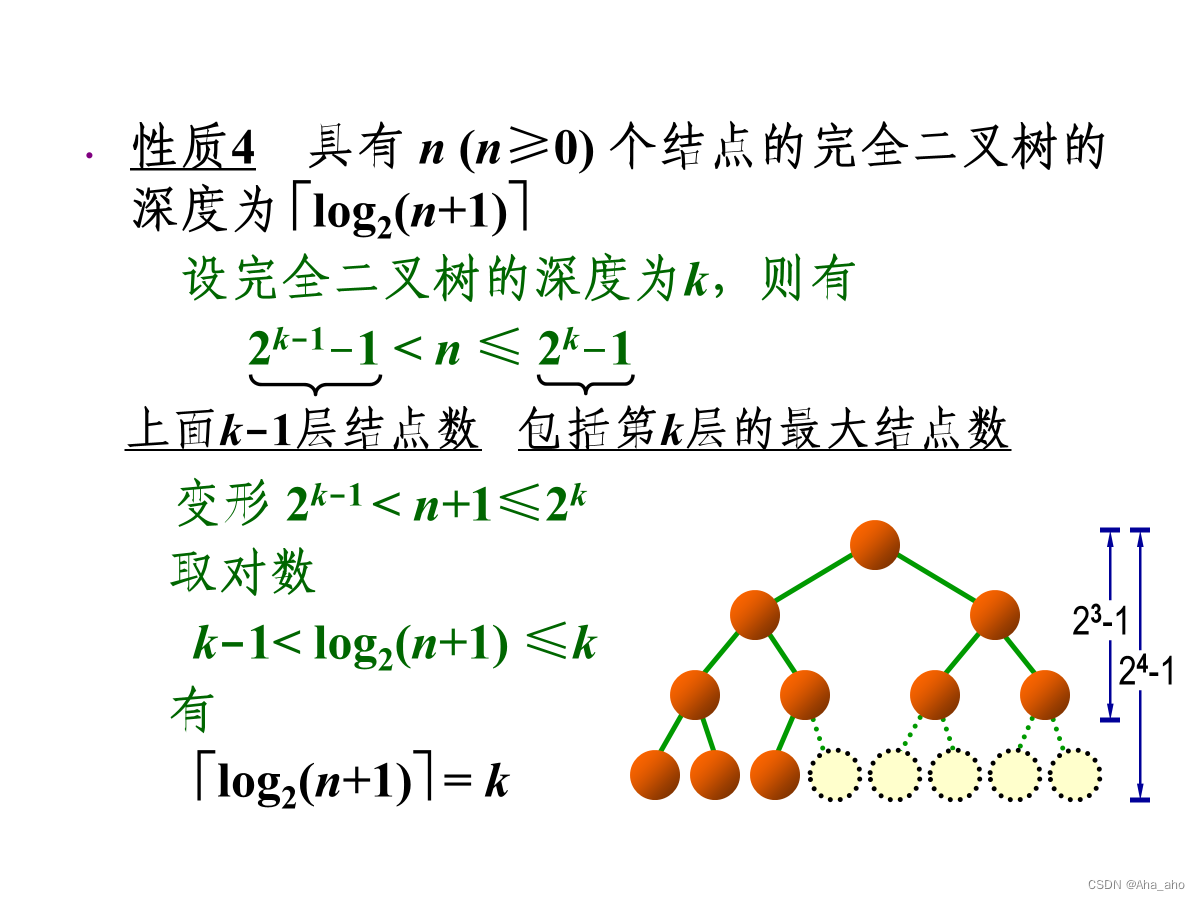
性质5：其实是堆

完全二叉树适合顺序表示。

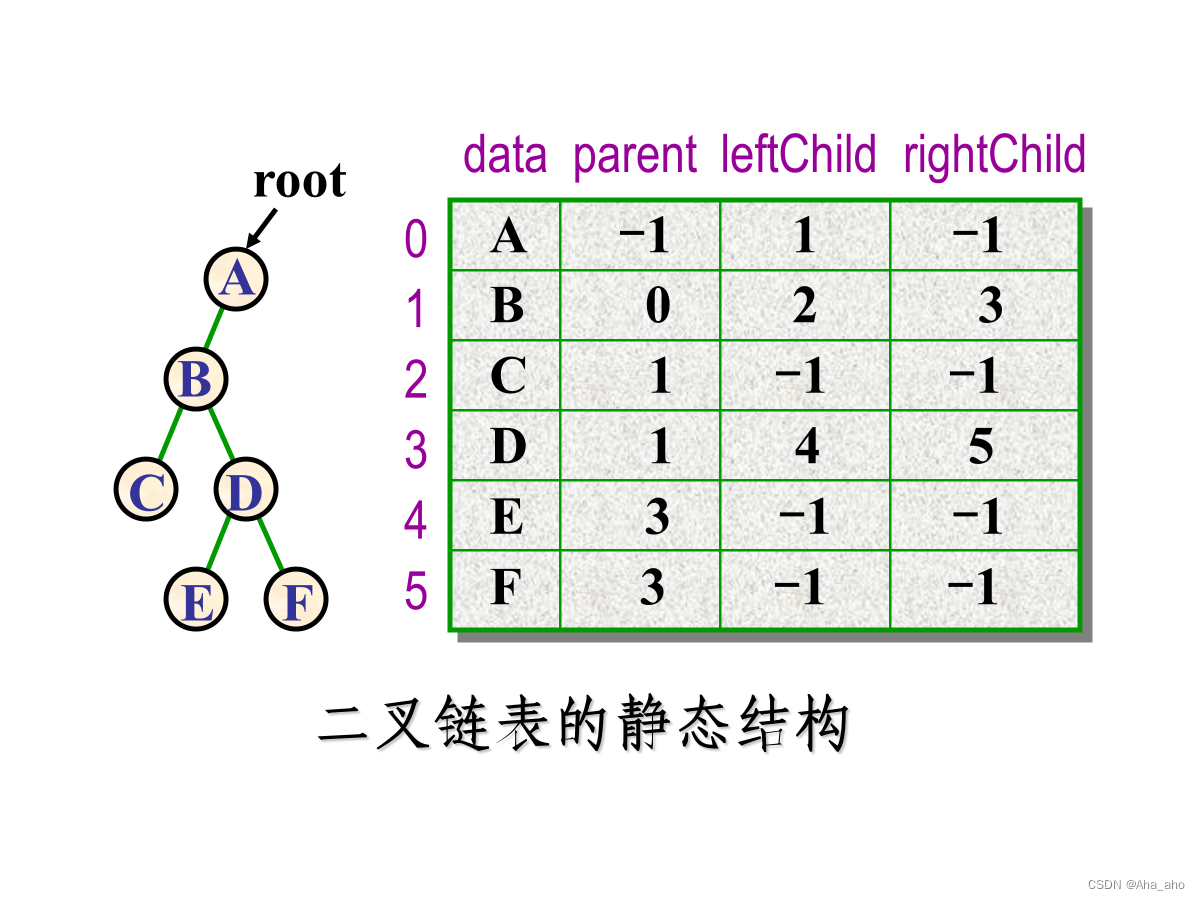
?二叉树的二叉链表表示（最为常用）

要会二叉链表的静态结构转换

二叉树的遍历：?

前序 ? VLR ? ?根左右
中序 ? LVR ? ?左根右
后序 ? LRV ? ?左右根

在树的学习中，递归的思想很重要！

前中后序的递归与非递归实现

非递归实现：依赖栈

层序遍历

非递归的，借助一个队列

3、线索化二叉树

目的

希望不必每次都通过遍历找出遍历的线性序列。只要事先做预处理，将某种遍历顺序下的前驱、后继关系记在树的存储结构中，以后就可以高效地找出某结点的前驱、后继。

示例：

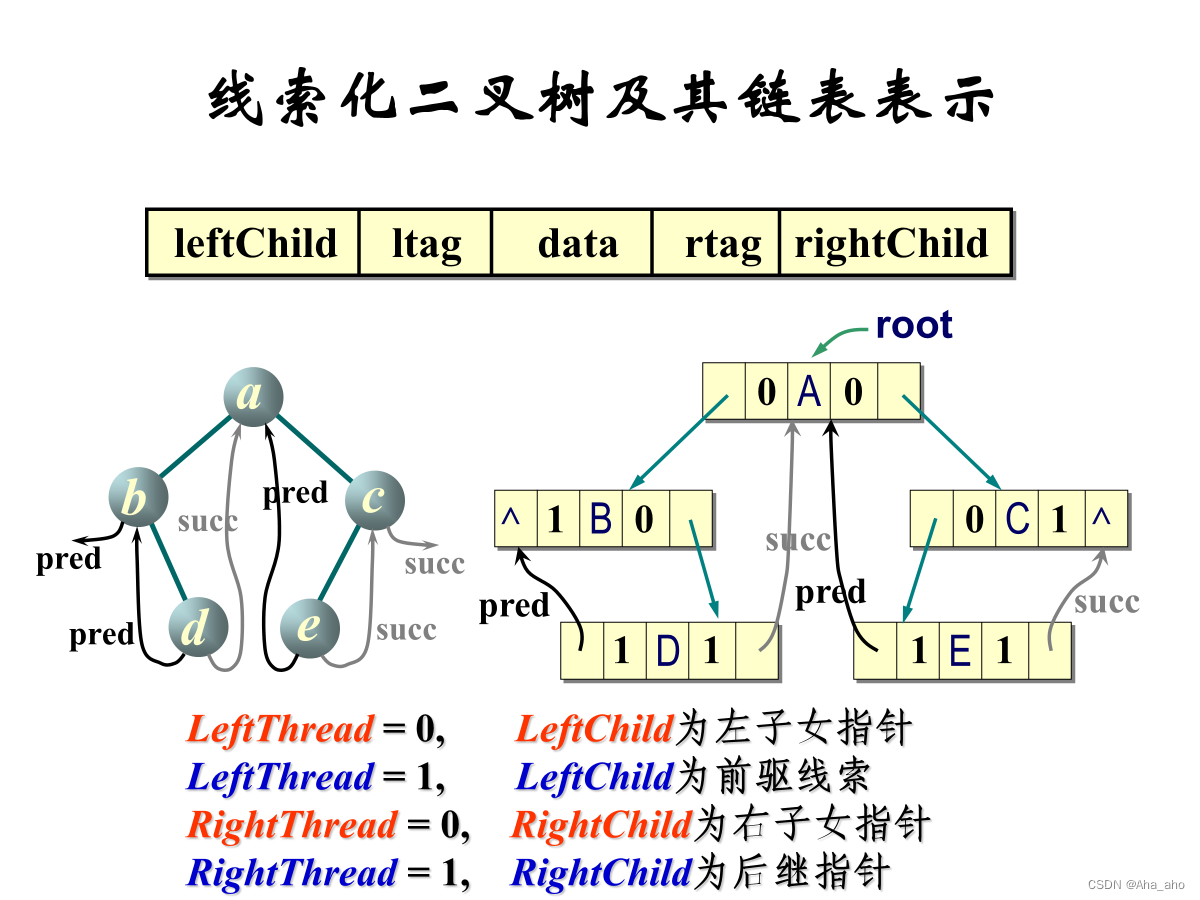
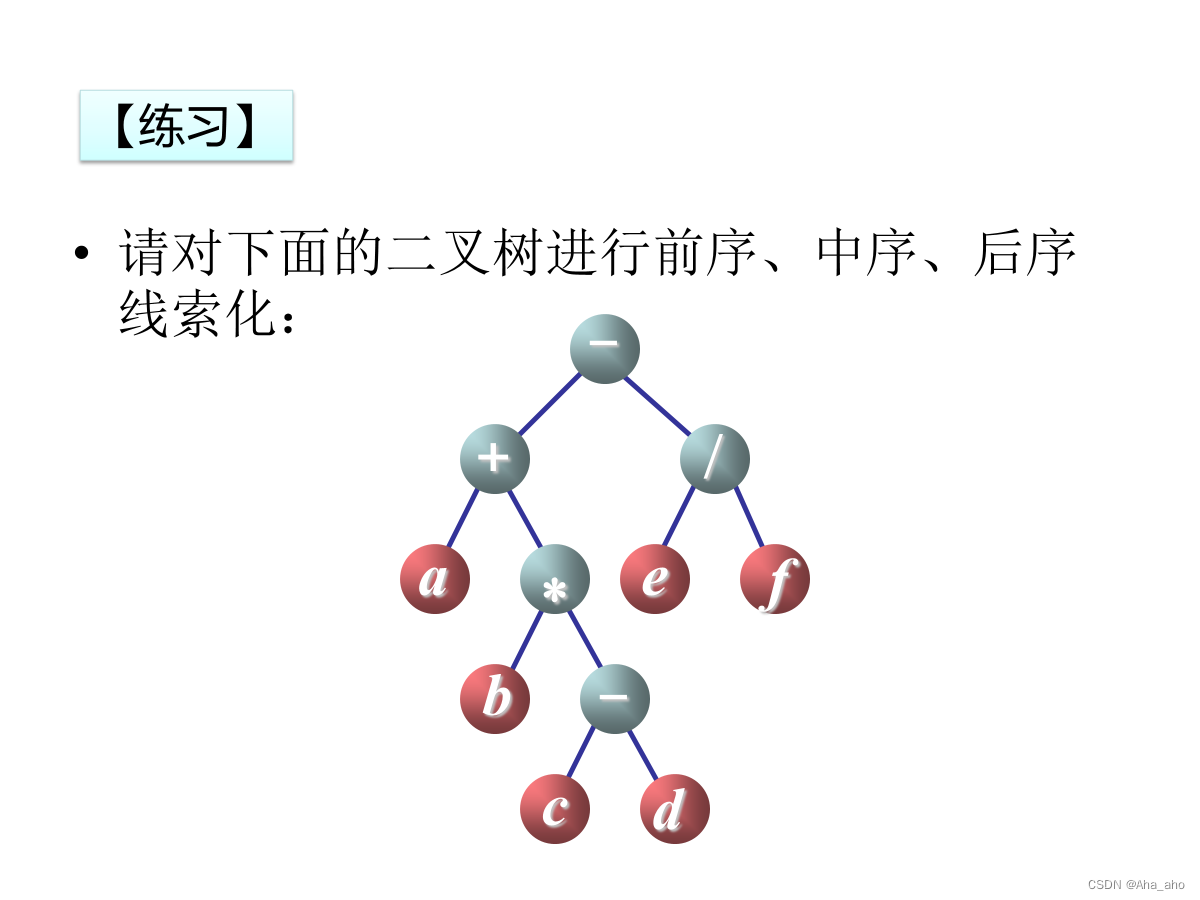
练习题思路：

先写出前序、中序、后序的正确序列，再线索化。

?

一道练习：

一棵左右子树均不空的二叉树在先序线索化后，其中空的链域的个数是： （??? ）。

A. 0??????????? B. 1??????? C. 2????????? D. 不确定

答案：B

解析：

左右子树都存在的情况下进行二叉树的线索化，依据一下原则：

先序线索化：根 左 右 NULL

中序线索化：NULL 左 根 右 NULL

后序线索化：NULL 左 右 根

如果这道练习中的二叉树只有右子树、没有左子树，则此题的空指针域数为2。

4、树与森林

仅介绍左子女右兄弟表示法

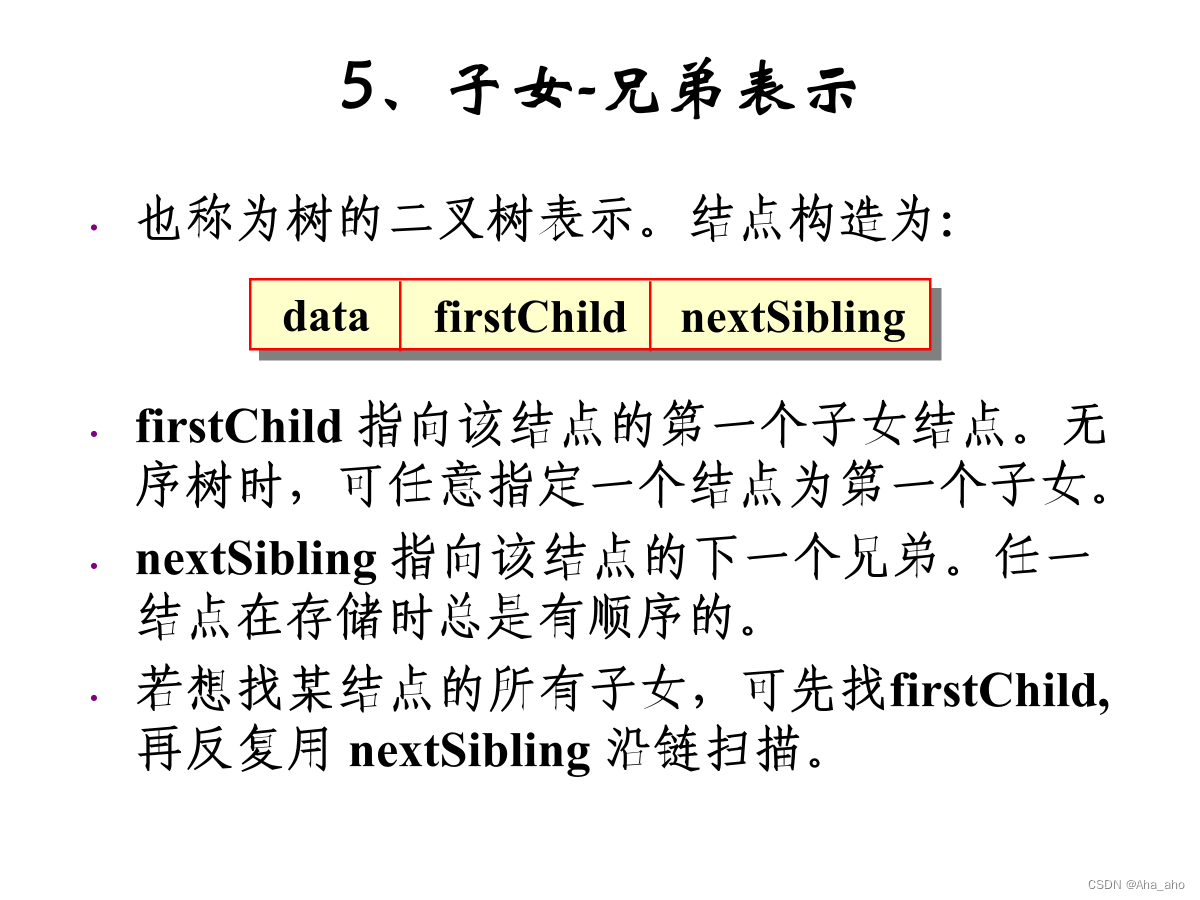
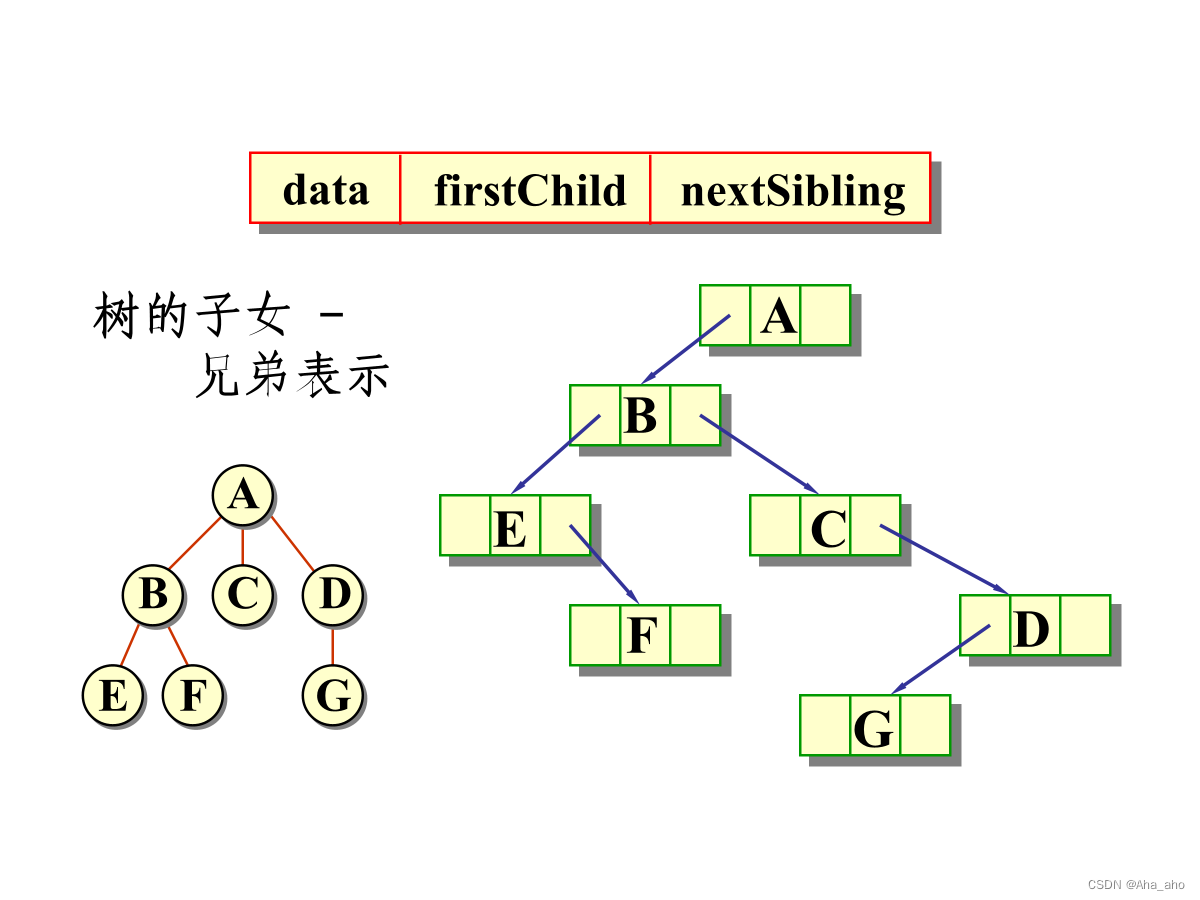
树的遍历：

先根：前序?

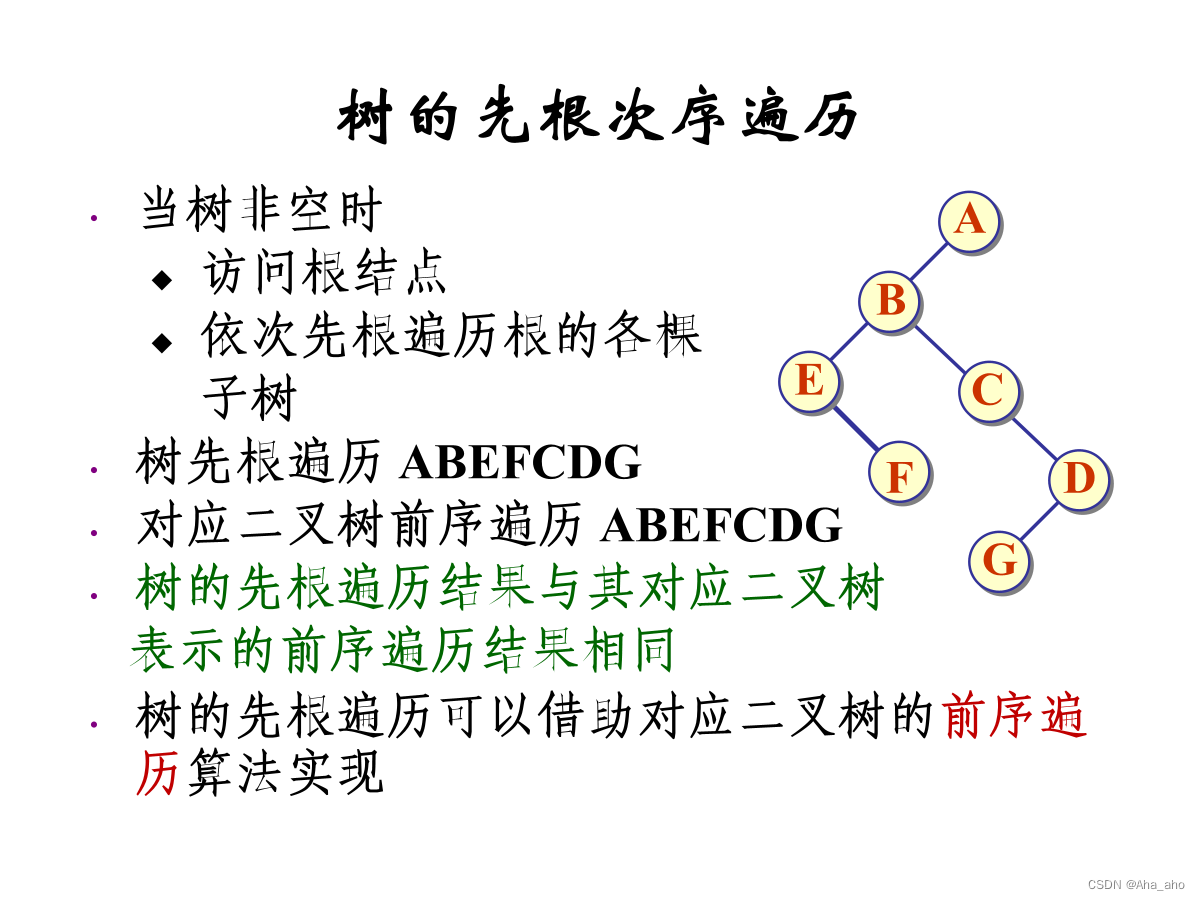
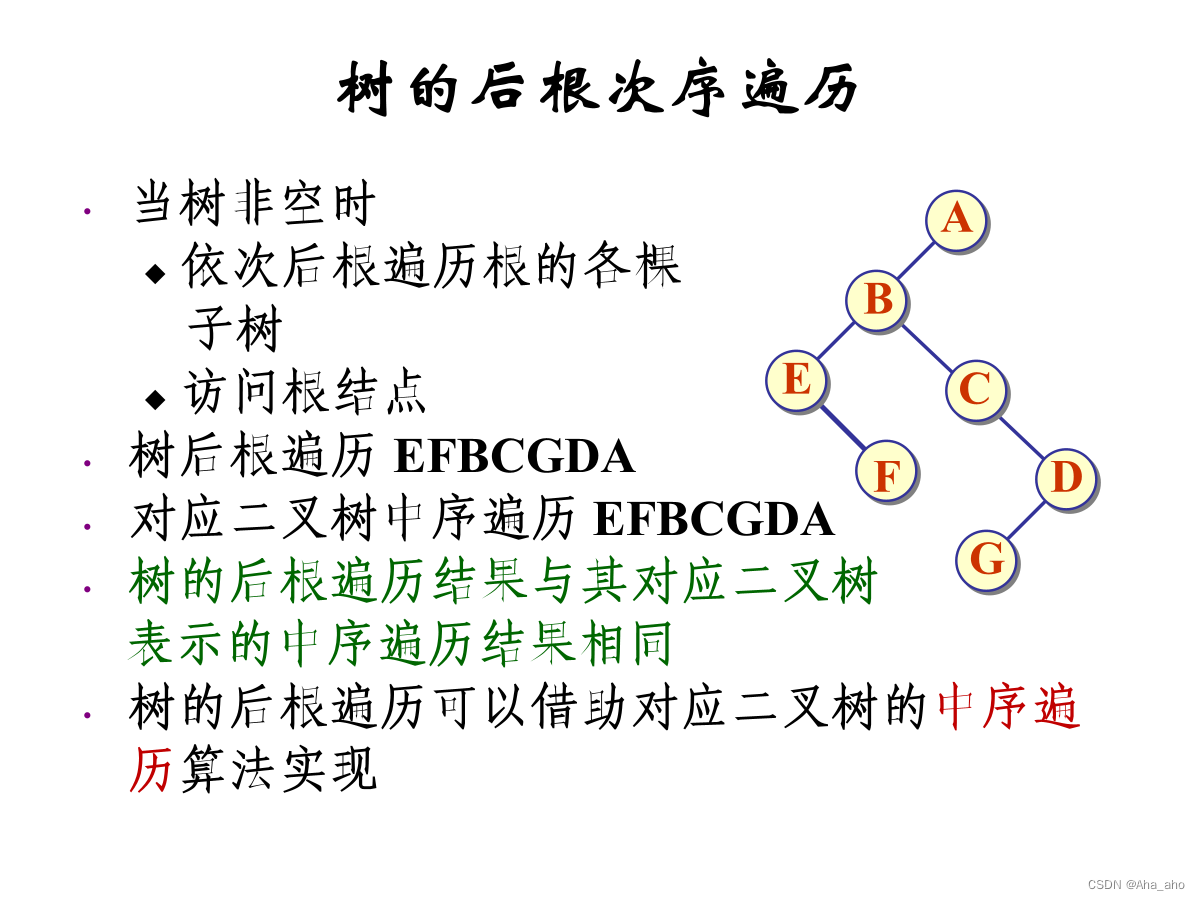
?后根：中序

广度优先：借助队列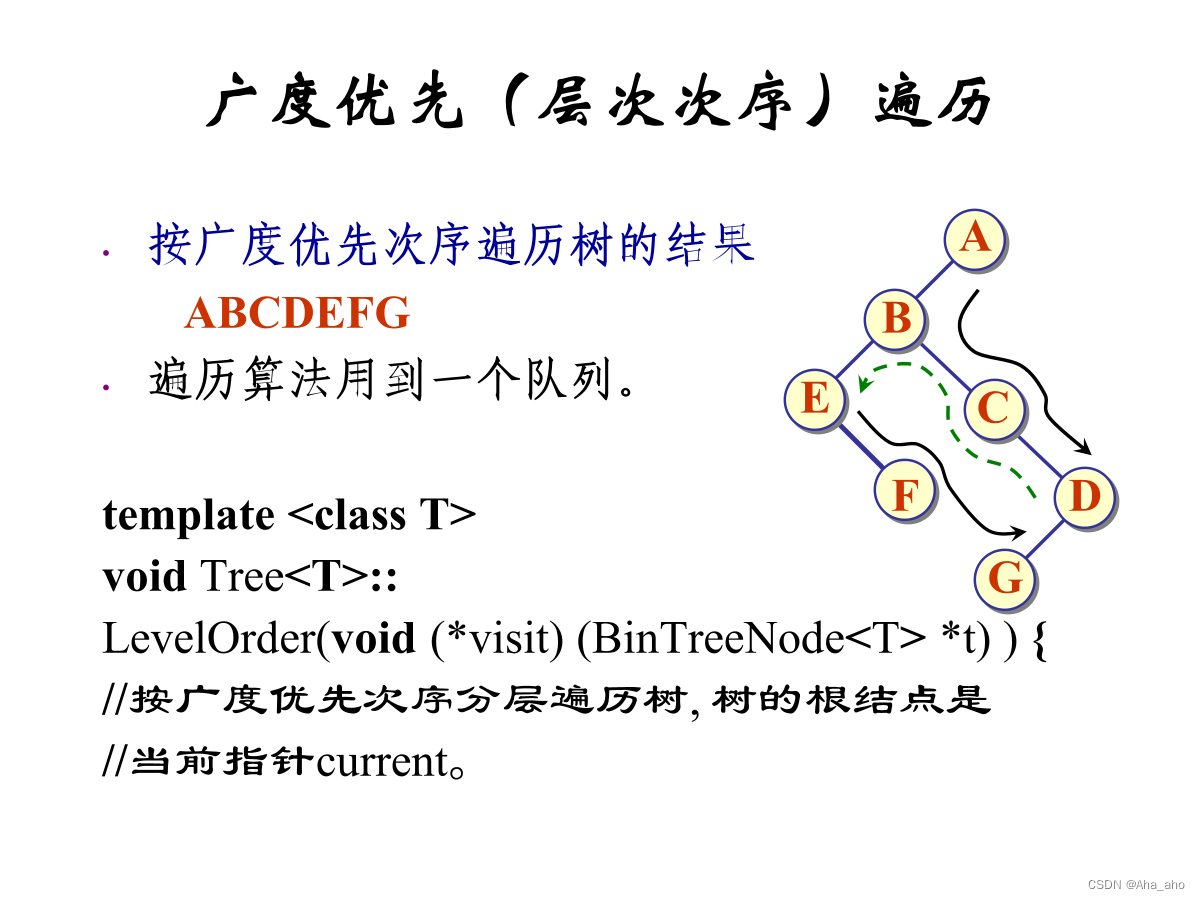

森林与二叉树的转换

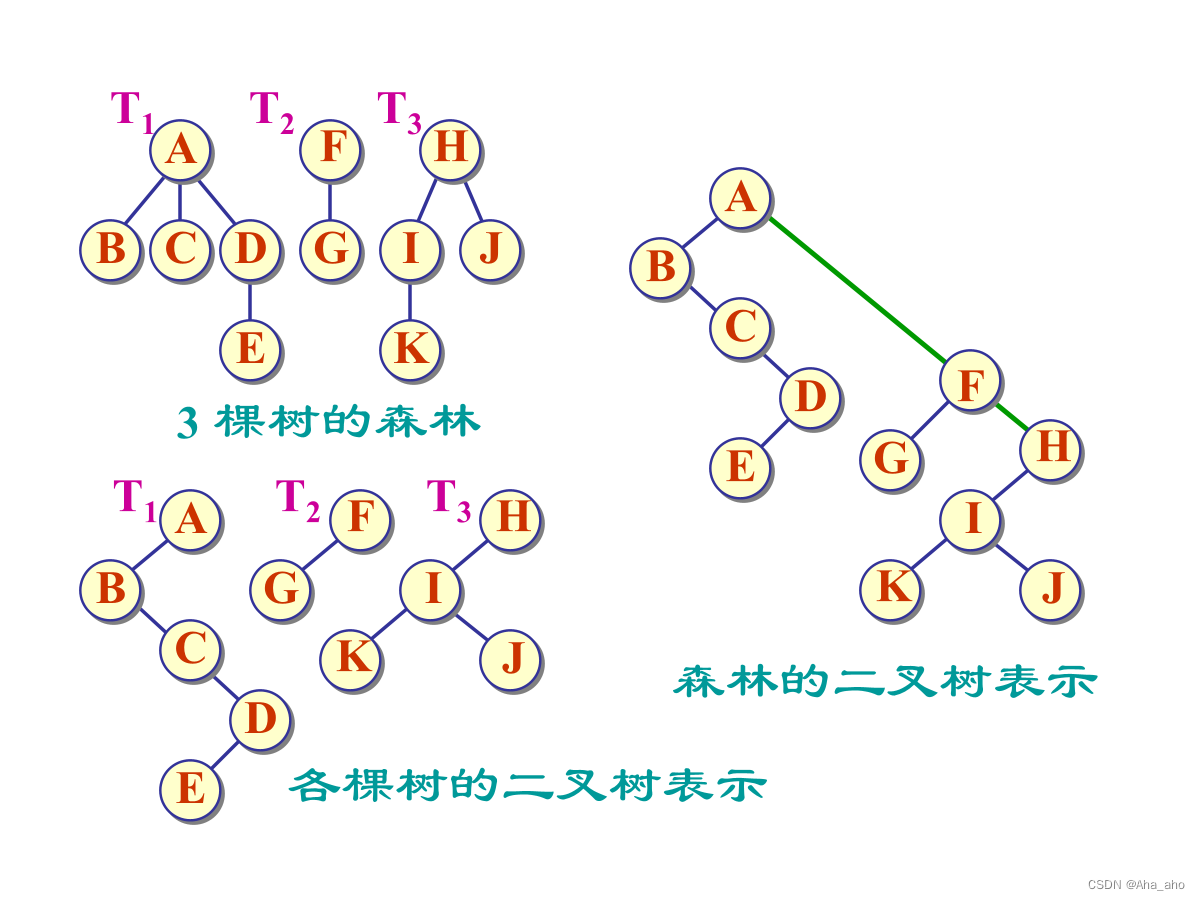
5、堆?

是优先级队列的一种实现方式。

堆的建立：

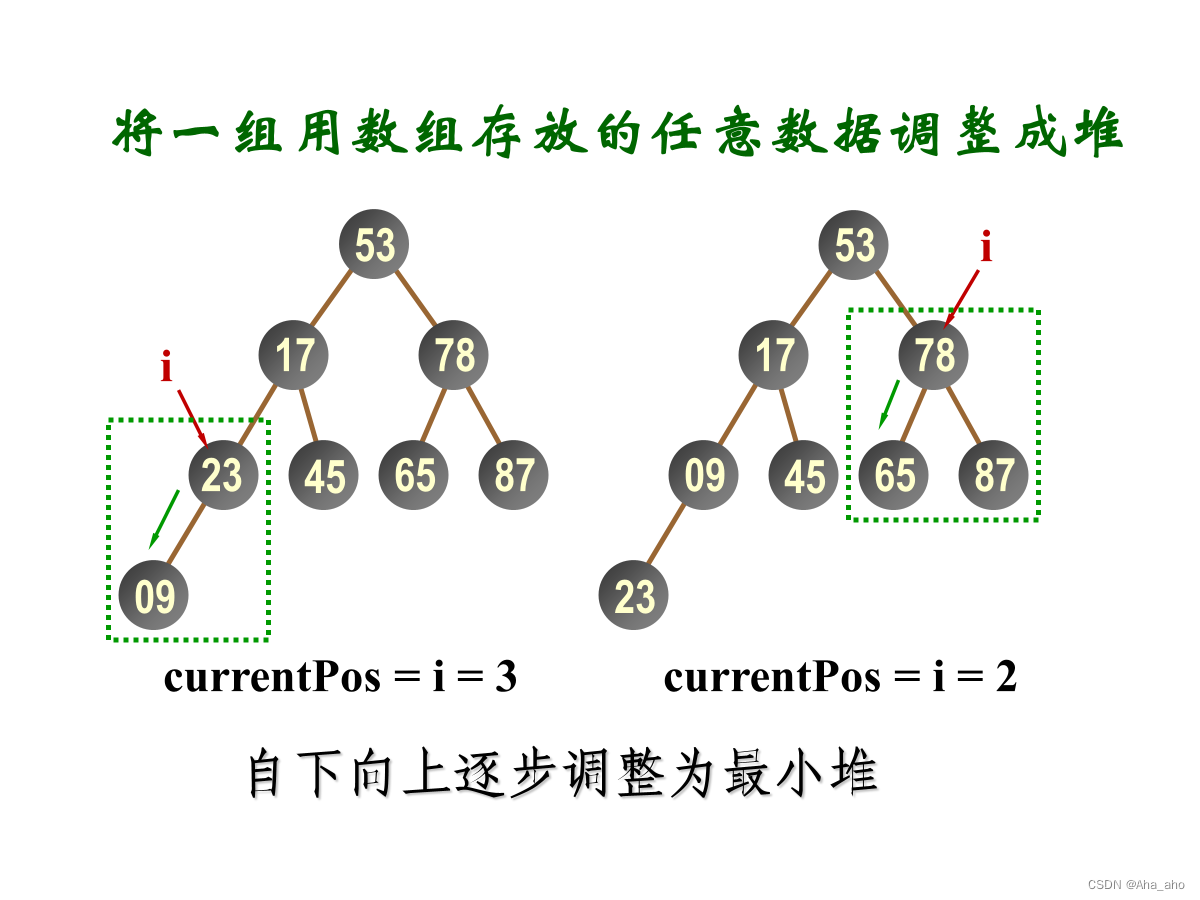
将一组用数组存放的任意数据调整成堆

template <class T, class E>
MinHeap<T>::MinHeap (E arr[], int n) {
     maxHeapSize = (DefaultSize < n) ? n : DefaultSize;
     heap = new E[maxHeapSize]; 
	 if (heap == NULL) {
        cerr << “堆存储分配失败！” << endl;  exit(1);
     }
     for (int i = 0; i < n; i++) heap[i] = arr[i];
     currentSize = n;	       //复制堆数组, 建立当前大小
	 int currentPos = (currentSize-2)/2;	
                              //找最初调整位置:最后分支结点
     while (currentPos >= 0) {	    //逐步向上扩大堆
           siftDown (currentPos, currentSize-1);
           	//局部自上向下下滑调整
           currentPos--;
     }					
};

从某个节点开始向下调整的前提条件是假定它的两棵子树都已成为堆。

因此，将一维数组存放的任意数据调整成堆的方法为自下向上逐步调整为最小堆；

需要记住找最初调整位置的公式：?int currentPos = (currentSize-2)/2;?

?

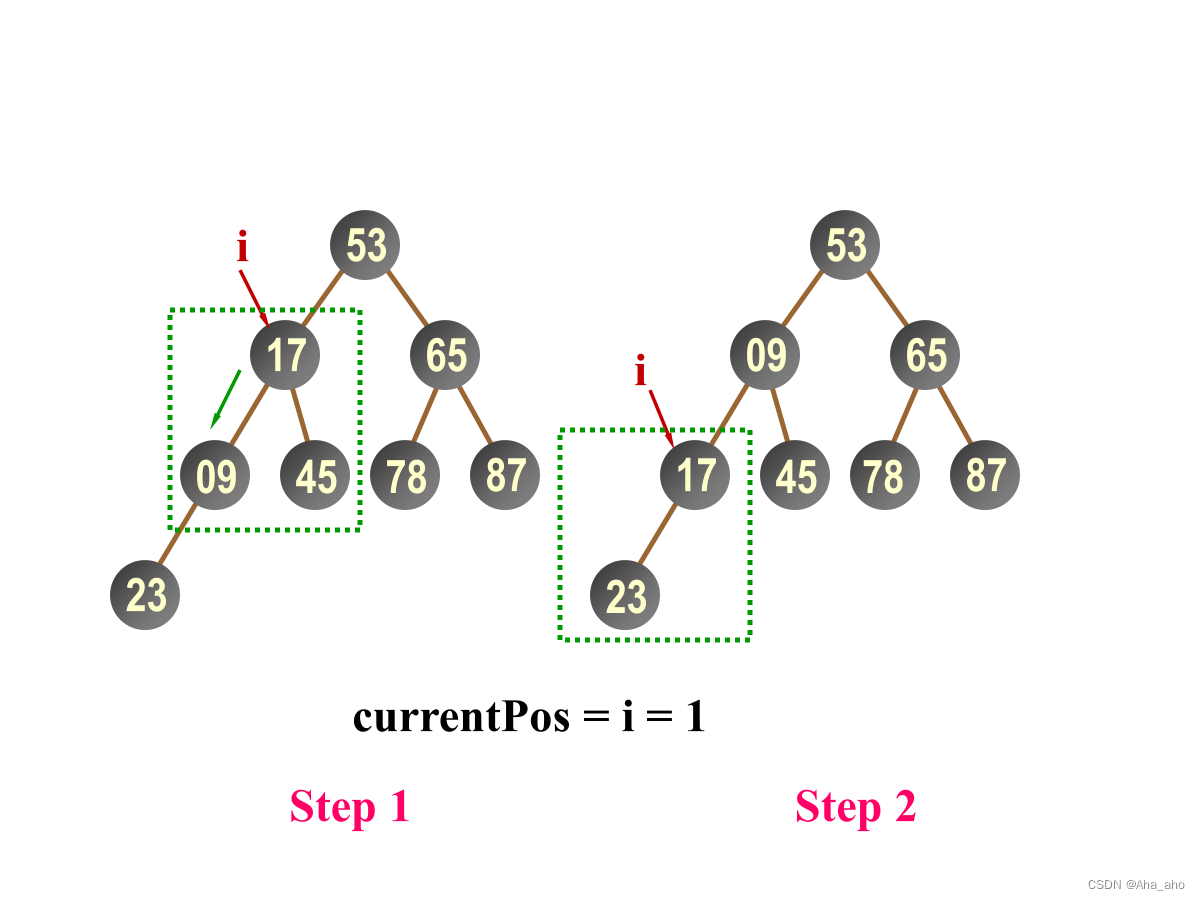
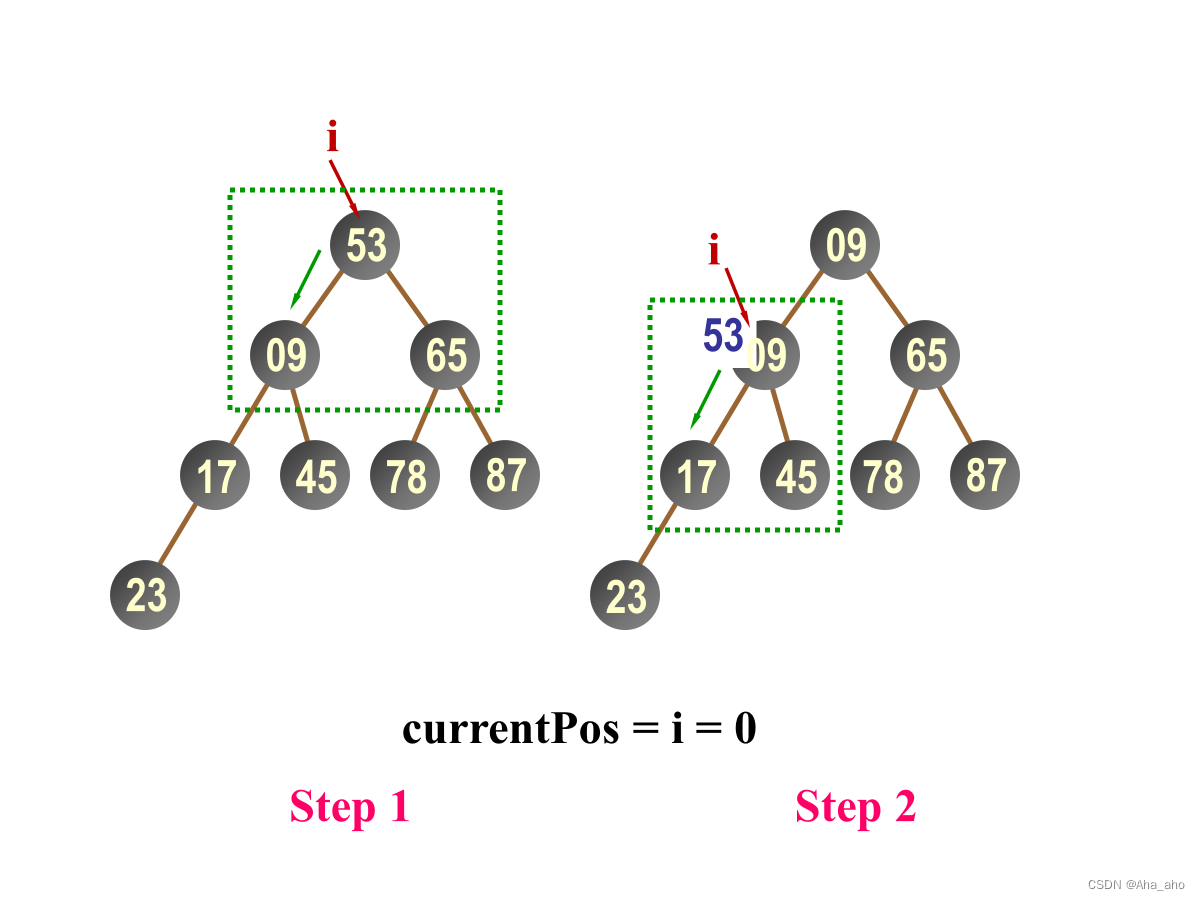
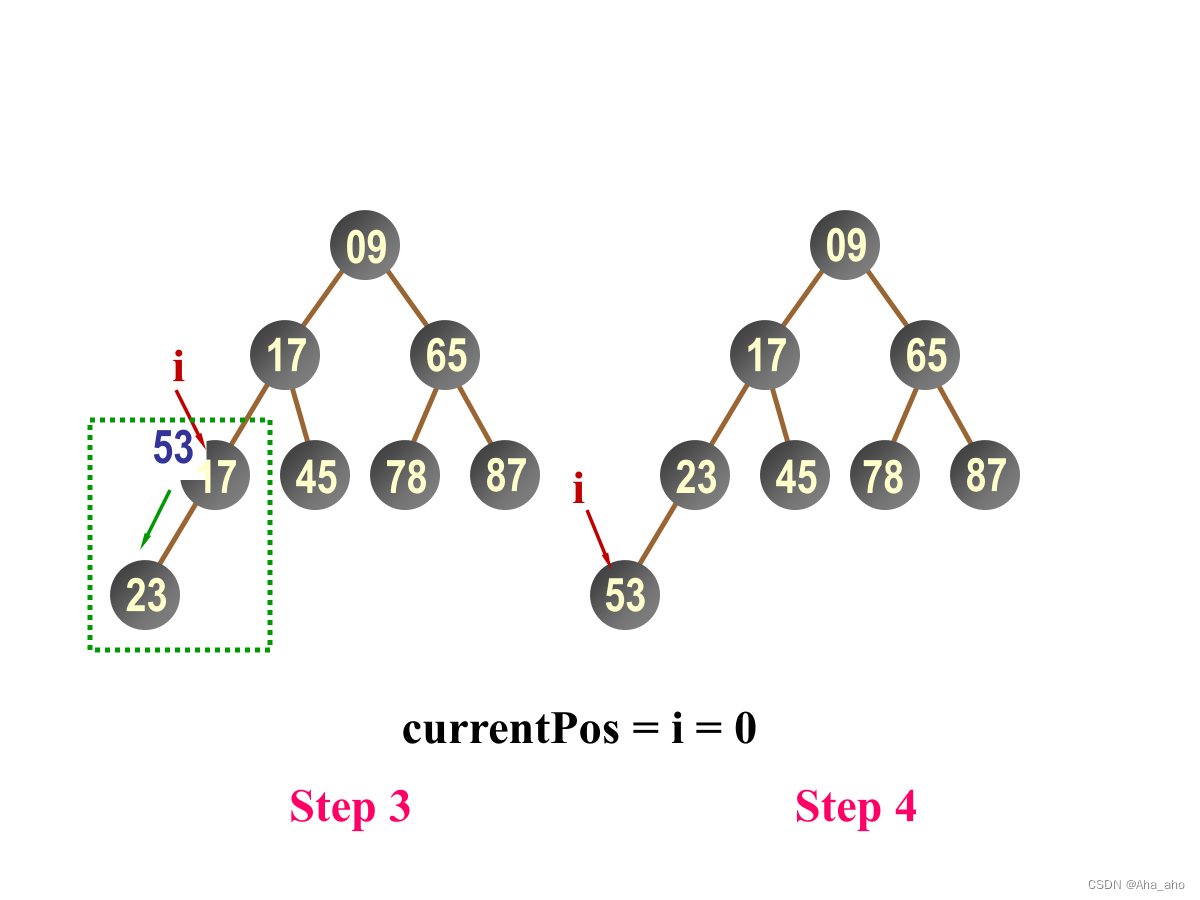
下滑调整算法

template <class T, class E>
void MinHeap<T>::siftDown (int start, int m ) {
//私有函数: 从结点start开始到m为止, 自上向下比较, 
//如果子女的值小于父结点的值,  则关键码小的上浮, 
//继续向下层比较, 将一个集合局部调整为最小堆。
	int i = start,   j = 2*i+1;  	//j是i的左子女位置
	E temp = heap[i]; 			
	while (j <= m) {			//检查是否到最后位置
	     if ( j < m && heap[j] > heap[j+1] ) j++;
				 	     //让j指向两子女中的小者
 		if ( temp <= heap[j] ) break;	//小则不做调整
		else { heap[i] = heap[j];  i = j; j = 2*j+1; }
				     	//否则小者上移, i, j下降
	 }
	 heap[i] = temp;	      	//回放temp中暂存的元素
};

?最小堆的插入

每次插入都加在堆的最后，再自下向上执行调整，使之重新形成堆，时间复杂性。

上浮调整

template <class T, class E>
void MinHeap<T>::siftUp (int start) {
//私有函数: 从结点start开始到结点0为止, 自下向上
//比较, 如果子女的值小于父结点的值, 则相互交换, 
//这样将集合重新调整为最小堆。关键码比较符<=
//在E中定义。
	 int j = start,  i = (j-1)/2;   E temp = heap[j];
	 while (j > 0) {		//沿父结点路径向上直达根
	      if (heap[i] <= temp) break;							//父结点值小, 不调整
		else { heap[j] = heap[i];  j = i;  i = (i-1)/2; }
					//父结点结点值大, 调整
	  }	
	heap[j] = temp;				//回送
};

最小堆的删除

?删除堆顶：用最后一个元素填补堆顶，再从堆顶siftdown调整。

6、Huffman树

路径长度概念：

两个结点之间的路径长度 PL 是连接两结点的路径上的分支数。
树的外部路径长度是各叶结点（外结点）到根结点的路径长度之和 EPL。
树的内部路径长度是各非叶结点（内结点）到根结点的路径长度之和 IPL。
树的路径长度 PL = EPL + IPL。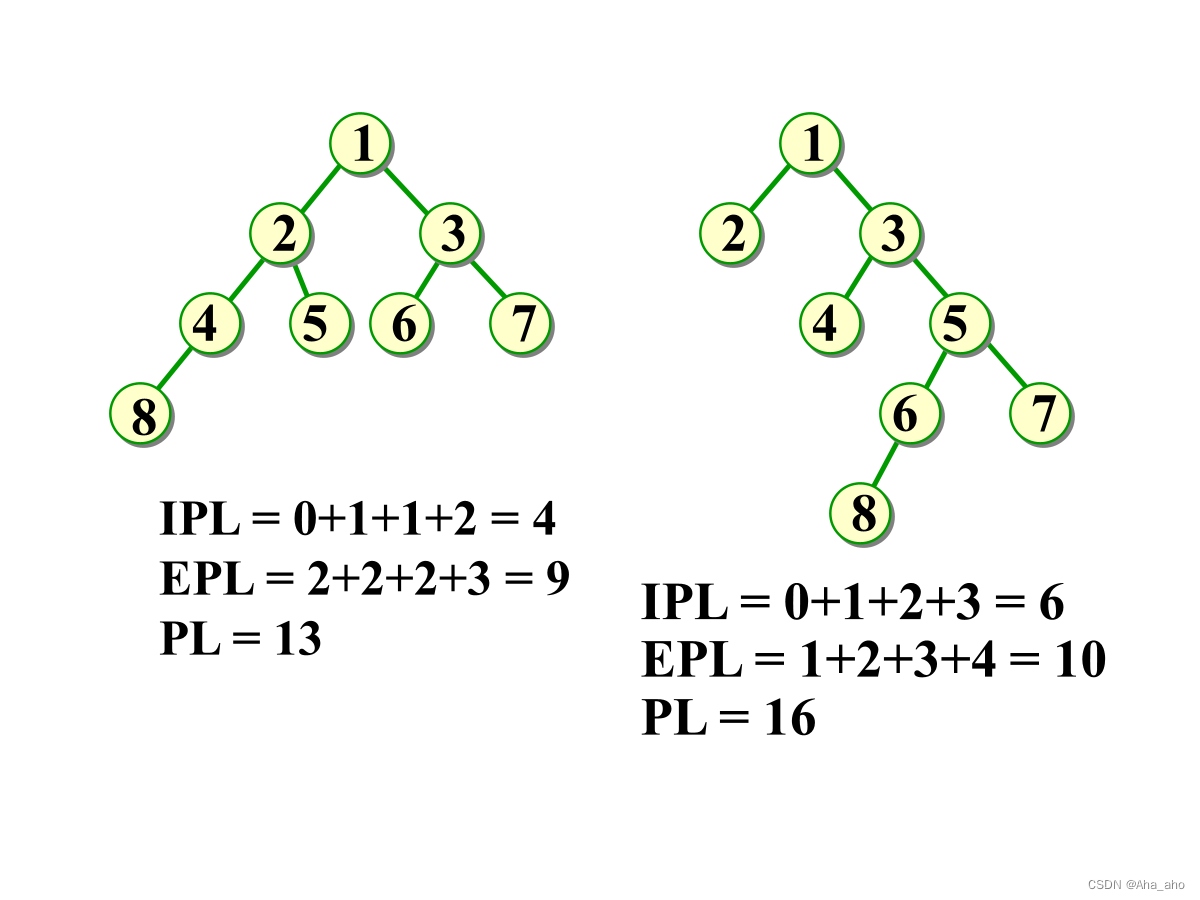

?完全二叉树的优势：

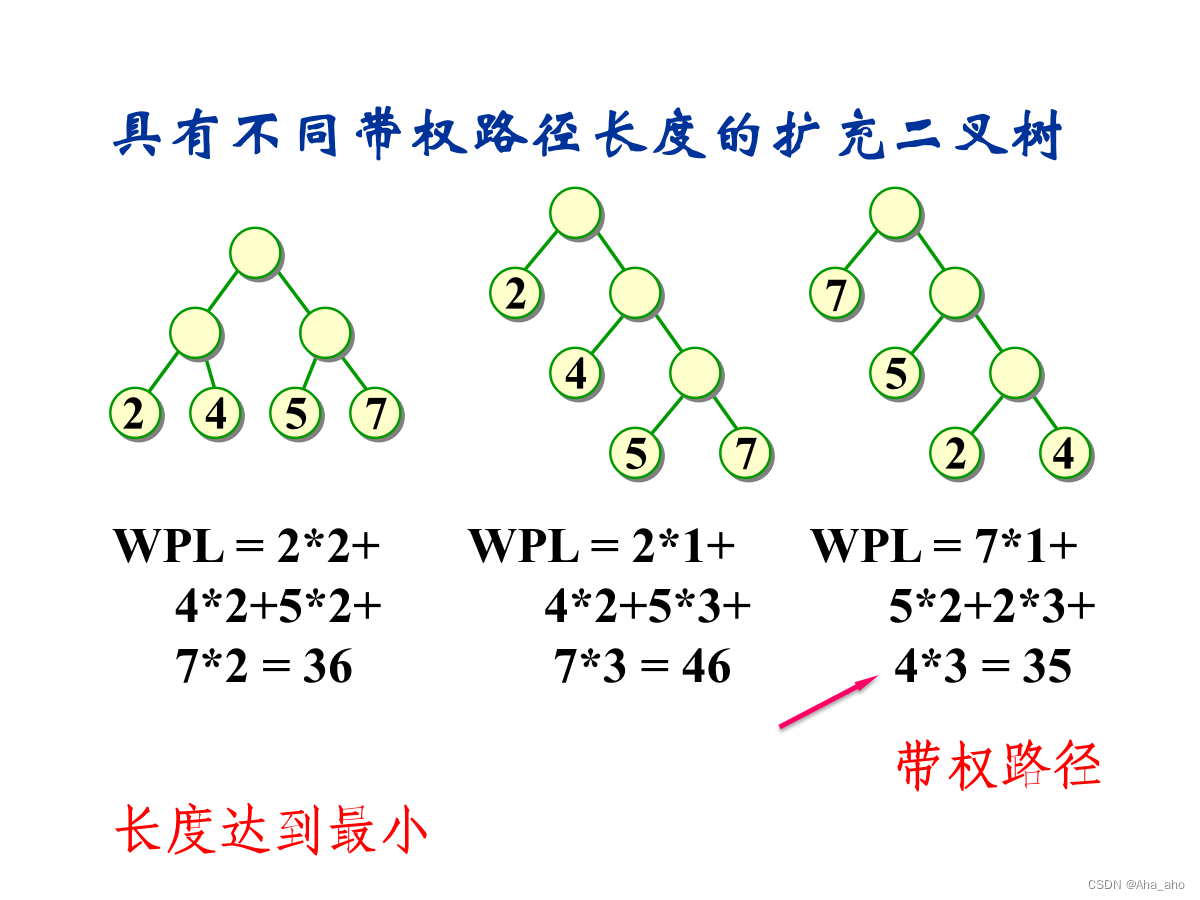
带权路径长度

?

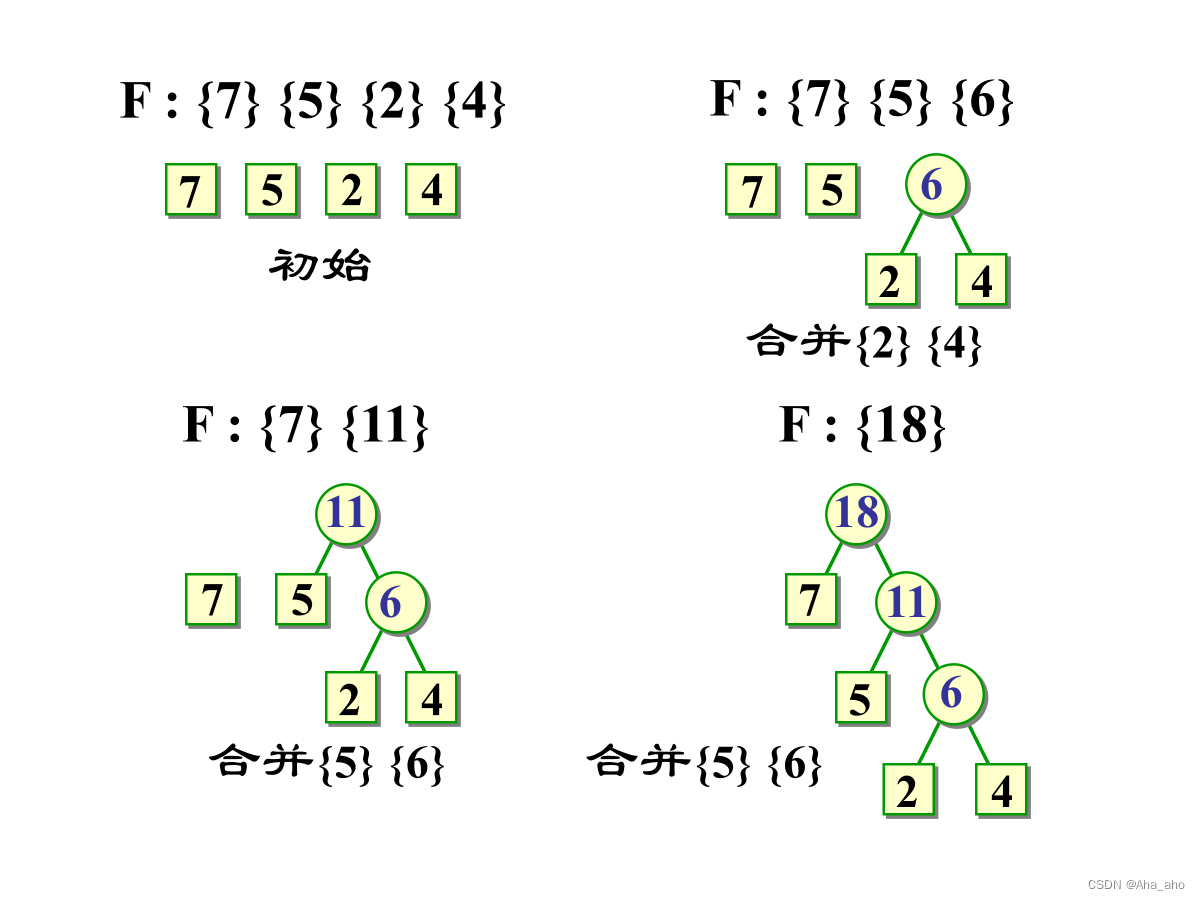
?Huffman树

带权路径长度达到最小的扩充二叉树即为Huffman树。

?

Huffman编码

?变长编码提高性能。

?