【强化学习-读书笔记】有限马尔可夫决策过程

参考 
Reinforcement Learning, Second Edition  
An Introduction 
By Richard S. Sutton and Andrew G. Barto

MDP 是强化学习问题在数学上的理想化形式，因为在这个框架下我们可以进行精确的理论说明

智能体与环境的交互

智能体与环境交互，会得到轨迹，根据轨迹长度$T$的情况，分为分幕式任务（$T<\infty$）和持续式任务（$T=\infty$）。轨迹的形式为：
$$S_0,A_0,R_1,S_1,A_1,R_2,S_2,A_2,...$$

---

回报（$G$ return）与奖励（$R$ reward）

$$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...$$
从$t+1$开始的原因：因为不存在$R_0$，但是存在$G_0$

---

状态价值函数$v_{\pi }(s)$ 与动作价值函数 $q_{\pi }(s,a)$

$$v_{\pi }(s)?\mathbb{E}[G_t|s]=\mathbb{E}[R_{t+1}+\gamma G_{t+1}|s]$$
$$q_{\pi }(s,a)?\mathbb{E}[G_t|s,a]=\mathbb{E}[R_{t+1}+\gamma G_{t+1}|s,a]$$
注意到$v,q$都定义成给定$\pi$这个分布的期望回报，因此都是理想存在的一个函数，而不是算法内部的。算法内部对他们两个函数的估计记作大写$V_{\pi }(S_t)$与$Q_{\pi }(S_t,A_t)$

---

策略函数 $\pi (a|s)$

策略是从状态到每个动作的选择概率之间的映射
$\pi (a|s)$ 中间的"|“只是提醒我们它为每个 s 都定义了一个在 a 上的概率分布

---

重要函数与公式

• 四参数动态函数
  $$p(s^{\prime },r|s,a)$$
  表示given $s$采取动作$a$，走到$s^{\prime }$并获得$r$的概率（对每一个不同的s,a组合，都有这样的一个函数）

• 状态转移概率
  $$p(s^{\prime }|s,a)=\sum _{r\in \mathcal{R}}p(s^{\prime },r|s,a)$$
• 状态-动作期望收益
  $$r(s,a)=\sum _{r\in \mathcal{R}}r\sum _{s^{\prime }\in \mathcal{S}}p(s^{\prime },r\mid s,a),$$
• 状态-动作-后继状态
  $$r(s,a,s^{\prime })=\sum _{r\in \mathcal{R}}r\frac{p(s^{\prime },r\mid s,a)}{p(s^{\prime }\mid s,a)}$$

• 用$\pi ,q$表示$v$
  $$v_{\pi }(s)?\sum _a\pi (a|s)q_{\pi }(s,a)$$
• 用$v$和四参数动态函数表示$q$
  $$q_{\pi }(s,a)=\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]$$

贝尔曼方程

• 状态价值函数的贝尔曼方程
  
• 动作价值函数的贝尔曼方程

看第二个等号，求和号里面第二项实际上就是$q_{\pi }$，因此
$$q_{\pi }(s,a)=\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]$$
$$=\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma \sum _{a^{\prime }}\pi (a^{\prime }|s^{\prime })q_{\pi }(s^{\prime },a^{\prime })]$$

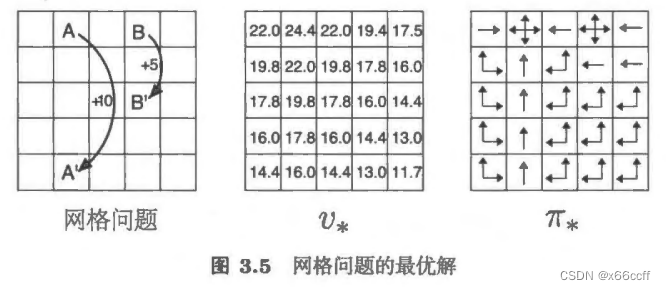
贝尔曼最优方程

$$v_{?}(s)=\underset{a}{\max }{q}_{?}(s,a)$$