123. 买卖股票的最佳时机 III

---

前言

在本文章中，我们将要详细介绍一下Leetcod 买卖股票的最佳时机 III相关的内容，本题采用动态规划的思想进行解决。

一、题目分析

给一个数组，找出最大利润
但是有两个条件：
??🌟不能同时参与多笔交易，手上只能有一只股票
??🌟最多完成两笔交易

二、算法原理

1.状态表示

列出dp表，dp表中值的含义是什么
dp[i]:代表在第i天获得的最大利润
这个又可以细分为两种状况：
?😾f[i]:第i天，手上有股票，处于买入状态，此时的最大利润。
?😾g[i]:第i天，手上无股票，处于卖出状态，此时的最大利润。

题目中要求最多完成两笔交易：又可以细分
?😾f[i][j]:在第i天，手上有股票，进行了j次交易，此时的最大利润
?😾g[i][j]:在第i天，手上无股票，进行了j次交易，此时的最大利润

2.状态转移方程

dp[i]是什么，根据最近一步划分问题
多状态可以相互转化，画图

?😾.在i-1天处于f状态，过了一天啥也不干，
此时最大利润，就是前一天的最大利润
?😾.在i-1天处于g状态，过了一天啥也不干，此时最大利润，就是前一天的最大利润
?😾.在i-1天处于g状态，第二天买了新股票，处于f状态，需要减去p[i],买东西要花钱，我们算的是利润
?😾.在i-1天处于f状态，第二天卖出股票，处于g状态，买了就会有钱，但是这是在上一次交易到这一次交易获得的钱，需要用（j-1）次交易时的最大利润进行计算

f[i][j]=max(f[i-1][j],g[i-1[j]-p[i])
g[i][j]=max(g[i-1][j],f[i-1][j-1]+p[i])

3.初始化

g根据状态转移方程我们发现，我们需要初始化f第一行，g第一行和f的第一列。

我们能不能不对f第一列进行处理，只处理那两个呢？？
通过修改状态转移方程实现：
g[i][j]=max(g[i-1][j],f[i-1][j-1]+p[i])
?😾.当j>=1时，这个式子不会越界
?😾.当j= =0时，会产生越界，那我们单独处理j==0的情况不就行了。

if(j==0) g[i][j]=g[i-1][j]
else g[i][j]=max(g[i-1][j],f[i-1][j-1]+p[i])

f和g表第一行初始化为神魔呢??

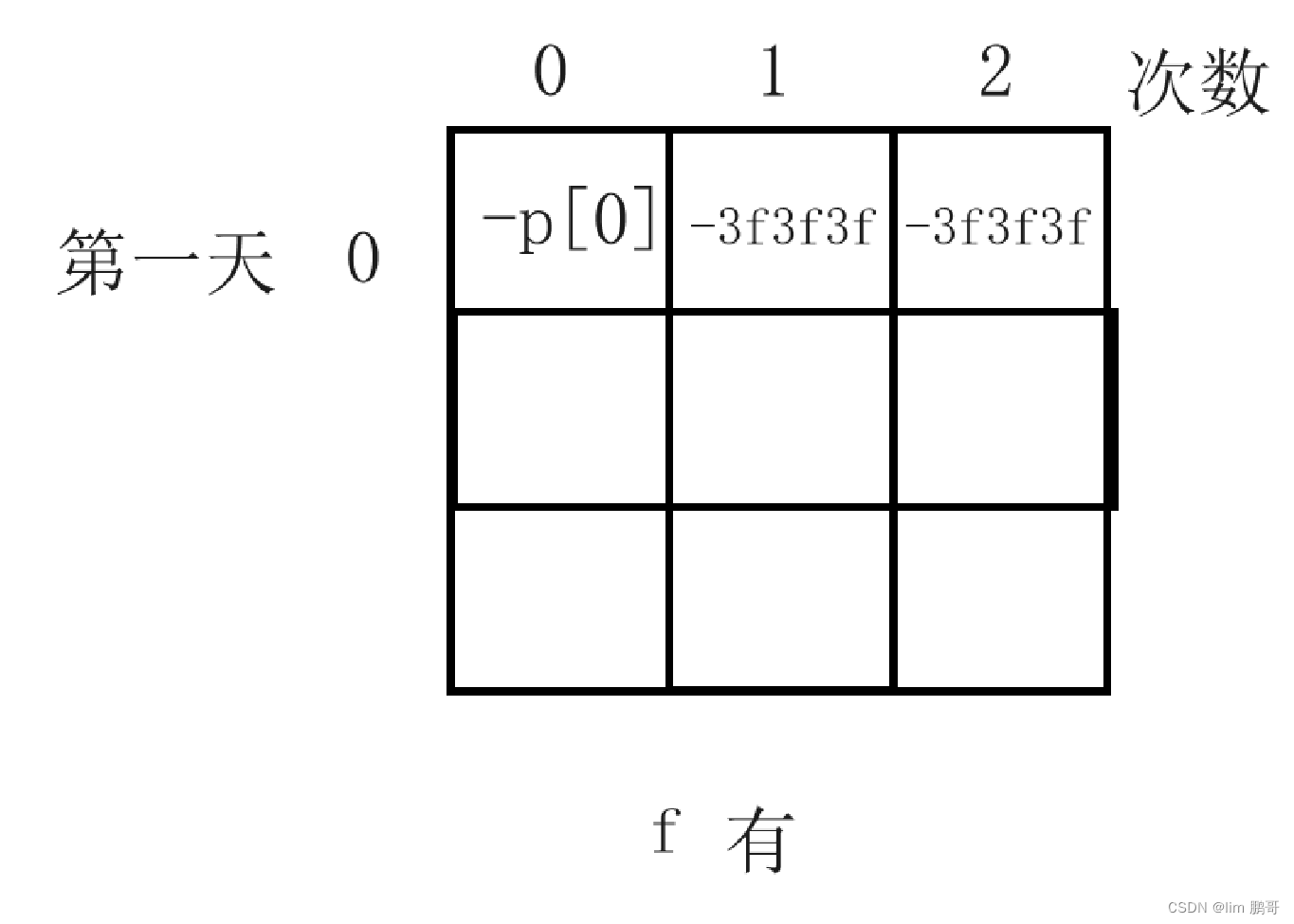
?😾.首先看一下f表
??🐯.f[0][0]:第一天有股票，那么肯定就购买了，就花钱了，所以f[0][0]=-p[0];
??🐯.第一行其他位置初始化为0可不可以呢？？
????如果为零，g[i][j]=max(g[i-1][j],f[i-1][j-1]+p[i])。如果g[0][1]大于f[0][0]+p[i]就会对这个式子就会产生影响，所以这里值不存在，我们在求的时候不要干扰max,那我们设置一个最小值（INT_MIN）不就行。
????如果是INT_MIN，对于这个表达式f[i][j]=max(f[i-1][j],g[i-1[j]-p[i])，最小值再减去一个值，就会发生越界。我们最好初始化为-0x3f3f3f3f(负整数的一半)。

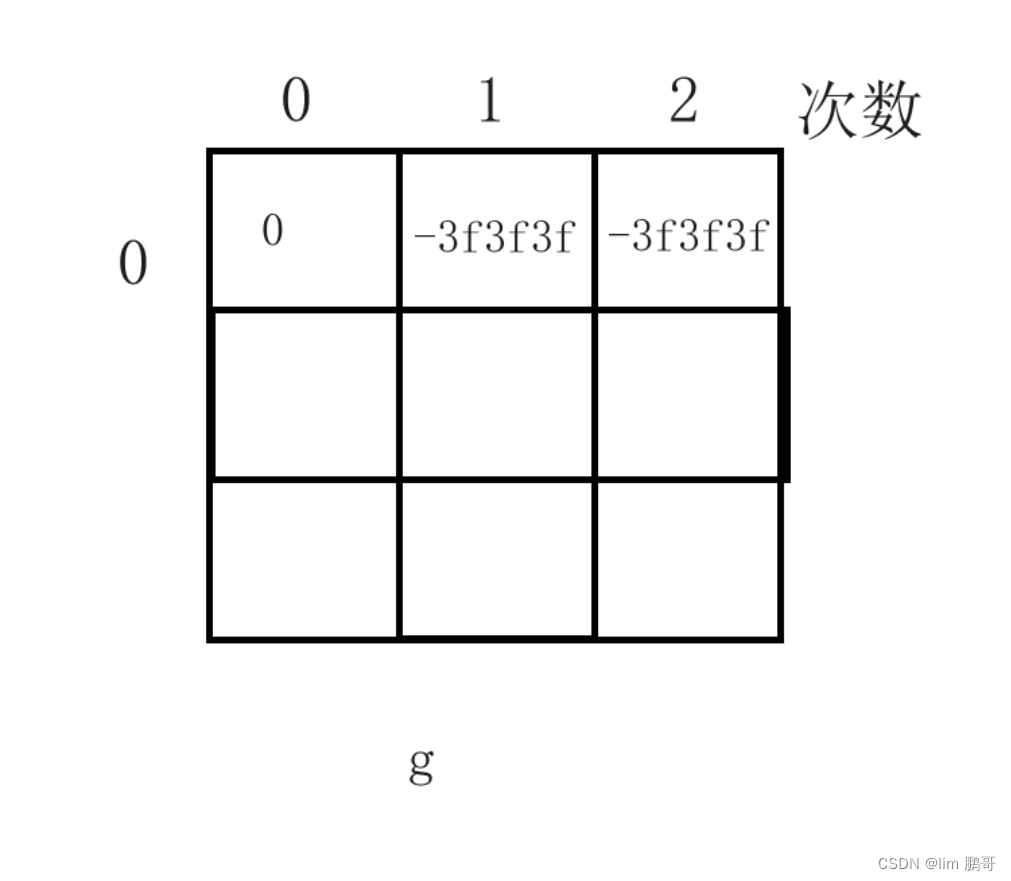
?😾.再看一下g表
??🐯.g[0][0]:第一天无股票，啥也没干，g[0][0]=0;
??🐯.对于其他位置，同上面f汾西方式一致，初始化为-3f3f3f3f

4.填表顺序

从上到下，从左往右，两个表一起填

5.返回值是什么

我们只知道处于g状态，手上没有股票时利润才最大
但是具体交易几次利润最大我们不清楚。
返回的最大值需要在最后一行进行查找。

三、代码实现

class Solution {
public:
    const int INT=0x3f3f3f3f;
    int maxProfit(vector<int>& p) 
    { 
        //建表
        int n=p.size();
        if(n==0)
        {
            return 0;
        }
        //创建+初始化
        vector<vector<int>> f(n,vector<int>(3,-INT));
        //怎莫写
        auto g=f;

        f[0][0]=0;
        g[0][0]=-p[0];
        //填表
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<3;j++)
            {
                g[i][j]=max(g[i-1][j],f[i-1][j]-p[i]);
                if(j==0)
                {
                    f[i][j]=f[i-1][j];
                }
                else
                {
                    f[i][j]=max(f[i-1][j],g[i-1][j-1]+p[i]);
                }
            }
        }
        //返回值
        int max=f[n-1][0];
        for(int j=1;j<3;j++)
        {
            if(f[n-1][j]>max)
            {
                max=f[n-1][j];
            }
        }
        return max;
    
    }
};

空间复杂度O（N）
时间复杂度O（N)

总结

以上就是我们对Leetcode中买卖股票的最佳时机 III详细介绍，希望对大家的学习有所帮助，仅供参考 如有错误请大佬指点我会尽快去改正 欢迎大家来评论~~