无约束优化问题求解(4):牛顿法后续
前言
Emm,由于上一篇笔记的字数超过了要求(这还是第一次- -),就把后续内容放到这篇笔记里面了,公式的标号仍然不变,上一篇笔记的连接在这:无约束优化问题求解(4):牛顿法
SR1, DFP, BFGS之间的关系
首先给出如下SMW公式:

考虑到 B k B_k Bk? 才是对Hessian矩阵的近似,如果我们能够知道每步对 Hessian矩阵的近似情况,那么将对收敛性分析有着很大的帮助.
SR1的有递推公式为
H
k
+
1
=
H
k
+
(
s
k
?
H
k
y
k
)
(
s
k
?
H
k
y
k
)
T
(
s
k
?
H
k
y
k
)
T
y
k
H_{k+1}=H_k+\frac{(s_k-H_ky_k)(s_k-H_ky_k)^T}{(s_k-H_ky_k)^Ty_k}
Hk+1?=Hk?+(sk??Hk?yk?)Tyk?(sk??Hk?yk?)(sk??Hk?yk?)T?两边取逆,使用SMW公式,可以得到SR1中,
B
k
B_k
Bk? 的迭代式
B
k
+
1
=
B
k
+
(
y
k
?
B
k
s
k
)
(
y
k
?
B
k
s
k
)
T
(
y
k
?
B
k
s
k
)
T
s
k
B_{k+1}=B_k+\frac{(y_k-B_ks_k)(y_k-B_ks_k)^T}{(y_k-B_ks_k)^Ts_k}
Bk+1?=Bk?+(yk??Bk?sk?)Tsk?(yk??Bk?sk?)(yk??Bk?sk?)T?可以发现,结果就是将
s
k
s_k
sk? 和
y
k
y_k
yk? 交换,把
B
k
B_k
Bk? 和
H
k
H_k
Hk? 交换。
因此,我们说SR1是自对偶的。
再看看DFP和BFGS迭代公式两边取逆后的结果:
D
F
P
:
H
k
+
1
=
H
k
+
s
k
s
k
T
s
k
T
y
k
?
H
k
y
k
y
k
T
H
k
y
k
T
H
k
y
k
B
k
+
1
=
B
k
+
(
1
+
s
k
T
B
k
s
k
s
k
T
y
k
)
y
k
y
k
T
s
k
T
y
k
?
(
y
k
s
k
T
B
k
+
B
k
s
k
y
k
T
s
k
T
y
k
)
B
F
G
S
:
H
k
+
1
=
H
k
+
(
1
+
y
k
T
H
k
y
k
s
k
T
y
k
)
s
k
s
k
T
s
k
T
y
k
?
(
s
k
y
k
T
H
k
+
H
k
y
k
s
k
T
s
k
T
y
k
)
B
k
+
1
=
B
k
+
y
k
y
k
T
y
k
T
s
k
?
B
k
s
k
s
k
T
B
k
s
k
T
B
k
s
k
\begin{aligned} \mathrm{DFP}:H_{k+1}& =H_k+\frac{s_ks_k^T}{s_k^Ty_k}-\frac{H_ky_ky_k^TH_k}{y_k^TH_ky_k} \\ B_{k+1}& =B_k+\left(1+\frac{s_k^TB_ks_k}{s_k^Ty_k}\right)\frac{y_ky_k^T}{s_k^Ty_k}-\left(\frac{y_ks_k^TB_k+B_ks_ky_k^T}{s_k^Ty_k}\right) \\ \mathrm{BFGS}:H_{k+1}& =H_k+\left(1+\frac{y_k^TH_ky_k}{s_k^Ty_k}\right)\frac{s_ks_k^T}{s_k^Ty_k}-\left(\frac{s_ky_k^TH_k+H_ky_ks_k^T}{s_k^Ty_k}\right) \\ B_{k+1}& =B_k+\frac{y_ky_k^T}{y_k^Ts_k}-\frac{B_ks_ks_k^TB_k}{s_k^TB_ks_k} \end{aligned}
DFP:Hk+1?Bk+1?BFGS:Hk+1?Bk+1??=Hk?+skT?yk?sk?skT???ykT?Hk?yk?Hk?yk?ykT?Hk??=Bk?+(1+skT?yk?skT?Bk?sk??)skT?yk?yk?ykT???(skT?yk?yk?skT?Bk?+Bk?sk?ykT??)=Hk?+(1+skT?yk?ykT?Hk?yk??)skT?yk?sk?skT???(skT?yk?sk?ykT?Hk?+Hk?yk?skT??)=Bk?+ykT?sk?yk?ykT???skT?Bk?sk?Bk?sk?skT?Bk???可以发现只要
s
k
?
y
k
,
B
k
?
H
k
s_{k}\leftrightarrow y_{k},B_{k}\leftrightarrow H_{k}
sk??yk?,Bk??Hk?,就可以在DFP和BFGS公式之间相互转换。因此,我们说DFP和BFGS互为对偶的。
设需要优化的目标函数如下:
min
?
f
(
x
)
=
∑
i
=
1
4
r
i
(
x
)
2
\min f(x)=\sum_{i=1}^4r_i(x)^2
minf(x)=i=1∑4?ri?(x)2其中
r
2
i
?
1
(
x
)
=
10
(
x
2
i
?
x
2
i
?
1
2
)
,
r
2
i
(
x
)
=
1
?
x
2
i
?
1
r_{2i-1}(x)=10(x_{2i}-x_{2i-1}^2),r_{2i}(x)=1-x_{2i-1}
r2i?1?(x)=10(x2i??x2i?12?),r2i?(x)=1?x2i?1? ,
x
∈
R
4
x\in\mathbb{R}^4
x∈R4 ,
x
k
x_k
xk? 代表向量
x
x
x 的第
k
k
k 个维度上的元素。
我们可以看出上述的优化问题的最优点为 ( 1 , 1 , 1 , 1 ) T (1,1,1,1)^T (1,1,1,1)T(可能有读者想知道怎么看出来的,只需要对每个分量求导,并令每个分量的一阶偏导数 ? f ? x i = 0 \frac{\partial f}{\partial x_i}=0 ?xi??f?=0,求解出来的点便是可能的极值点) , 取迭代初值为 x 0 = ( 2 , 0 , 3 , 4 ) T x_0=(2,0,3,4)^T x0?=(2,0,3,4)T 。我们首先先实现上述的函数,我通过一个函数获取一个映射 f : f: f:
from scipy.optimize import fmin_powell, fmin_bfgs, fmin_cg, minimize, SR1
import numpy as np
import matplotlib.pyplot as plt
?
# 定义函数
def r(i, x):
if i % 2 == 1:
return 10 * (x[i] - x[i - 1] ** 2) # 因为ndarray数组的index是从0开始的, i多减一个
else:
return 1 - x[i - 2]
?
def f(m):
def result(x):
return sum([r(i, x) ** 2 for i in range(1, m + 1)])
return result # 返回函数值
为了观察拟牛顿法运行过程中迭代点的下降情况,我们需要计算损失的函数如下:
# 获取retall的每个点的值损失|f(x) - f(x^*)|
def getLosses(retall, target_point, func):
"""
:param retall: 存储迭代过程中每个迭代点的列表,列表的每个元素时一个ndarray对象
:param target_point: 最优点,是ndarray对象
:param func: 优化函数的映射f
:return: 返回一个列表,代表retall中每个点到最优点的欧氏距离
"""
losses = []
for point in retall:# 对于每一个迭代点的列表做循环
losses.append(np.abs(func(target_point) - func(point))) #绝对值做损失
return losses
scipy.optimize子库中的许多执行拟牛顿法的算子提供了call_back参数,该参数要求传入一个函数对象,在拟牛顿每步迭代完后,传入的call_back函数会被调用。由于使用SR1法的算子minimize无法返回迭代过程中的每一个迭代点(也就是retall),于是我们需要call_back函数来将迭代完的点传入外部的列表,从而获取SR1的retall。除此之外,我们可以使用call_back函数来指定迭代停止的条件。
我们编写一个返回函数对象的函数,它会根据我们传入参数的不同返回不同的call_back函数:
sr1_losses = [] # 存储SR1的retall的列表
func = f(4) # 获取需要优化的函数
?
# 通过callback方法来添加迭代的停止条件
def getCallback(func, target_point, ftol, retall):
"""
:param func: 优化目标的函数
:param target_point: 目标收敛点
:param ftol: 收敛条件:|f(x) - f(x^*)| < ftol时,迭代停止
:param retall: 是否存储迭代信息
:param extern_retall: 如果retall为True, 填入一个列表,迭代信息会存在这个列表中
:return: call_back函数对象
"""
# 定义result函数
def result(xk, state=None):
if retall:
global func, sr1_losses # 对于SR1而言,需要声明全局变量来返回call_back对象
loss = np.abs(func(target_point) - func(xk))
if loss < ftol:
return True
else:
if retall: # 如果是SR1算法,则返回一个布尔值
sr1_losses.append(loss)
return False
return result # 如果不是SR1算法,则返回一个call_back对象
为了方便可视化,我们将数据可视化的逻辑封装到一个函数中:
# 绘制下降曲线
def plotDownCurve(dpi, losses, labels, xlabel=None, ylabel=None, title=None, grid=True):
plt.figure(dpi=dpi)
for loss, label in zip(losses, labels):
plt.plot(loss, label=label)
plt.xlabel(xlabel, fontsize=12)
plt.ylabel(ylabel, fontsize=12)
plt.title(title, fontsize=18)
plt.yscale("log")
plt.grid(grid)
plt.legend()
接着我们定义一下迭代初值、最优点和终止条件的阈值
?
\epsilon
? (
∣
f
(
x
k
+
1
)
?
f
(
x
k
)
∣
<
?
|f(x_{k+1})-f(x_k)|<\epsilon
∣f(xk+1?)?f(xk?)∣<? 时,迭代停止) 并获取三个拟牛顿法需要的 call_back函数。
x_0 = np.array([2,0,3,4]) # 迭代初值
target_point = np.array([1,1,1,1], dtype="float32") # 最优点
FTOL = 1e-8 # 终止阈值
?
sr1_callback = getCallback(func, target_point, ftol=FTOL, retall=True)
dfp_callback = getCallback(func, target_point, ftol=FTOL, retall=False)
bfgs_callback = getCallback(func, target_point, ftol=FTOL, retall=False)
下面使用minimum,fmin_powell,fmin_bfgs来实现三种拟牛顿法的迭代,并把DFP和BFGS的retall存入列表中。
# retall 是迭代点列,minimum是最终迭代点
minimum = minimize(fun=f(4), x0=x_0, # 通过minimize函数执行SR1,根据内嵌的callback填充loss,并返回OptimizerResult对象
method="trust-constr",
hess=SR1(),
callback=sr1_callback)
?
dfp_minimum, dfp_retall = fmin_powell(func=func, x0=x_0,
retall=True,
disp=False,
callback=dfp_callback)
dfp_losses = getLosses(dfp_retall, target_point, func=func)
?
bfgs_minimum, bfgs_retall = fmin_bfgs(f=func, x0=x_0,
retall=True,
disp=False,
callback=bfgs_callback)
bfgs_losses = getLosses(bfgs_retall, target_point, func=func)
我们可以调整plt画布的分辨率,设置一下各个轴的名称,然后将它可视化出来:
plotDownCurve(dpi=150,
losses=[sr1_losses, dfp_losses, bfgs_losses],
labels=["SR1", "DFP", "BFGS"],
xlabel="#iter",
ylabel="value of $|f(x) - f(x^*)|$",
title="losses curve of SR1, DFP and BFGS")
plt.show()
运行结果:
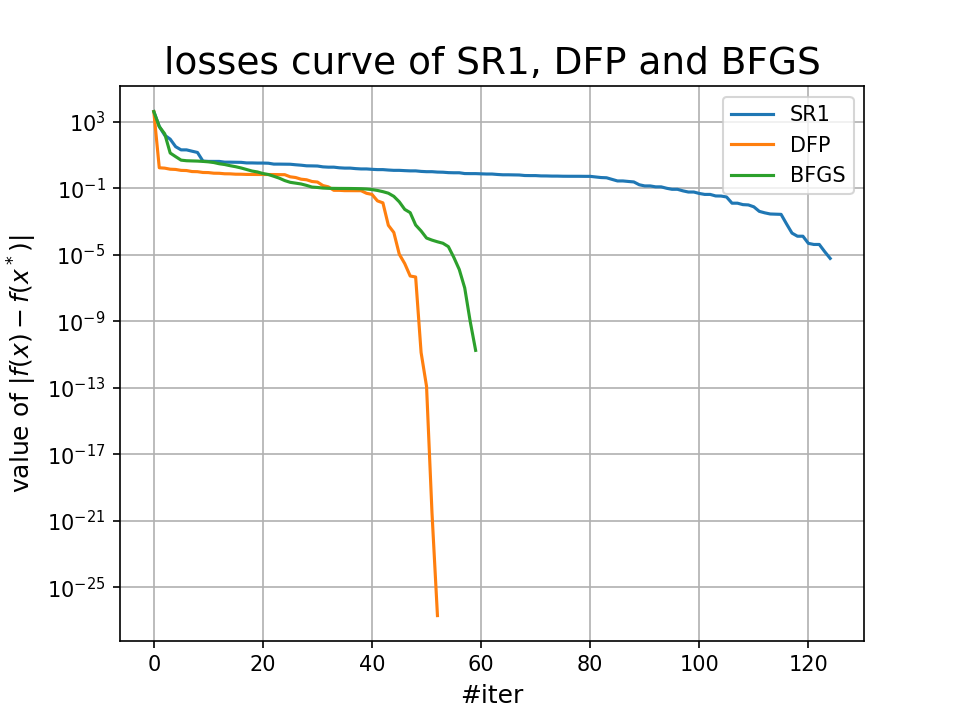
我们还可以查看三种方法得到的最优点和它们具体的迭代次数:
print(f"SR1\t最终迭代点:{minimum.x.tolist()}, 共经历{minimum.cg_niter}次迭代")
print(f"DFP\t最终迭代点:{dfp_minimum}, 共经历{len(dfp_losses)}次迭代")
print(f"BFGS\t最终迭代点:{bfgs_minimum}, 共经历{len(bfgs_losses)}次迭代")
运行结果:
SR1 最终迭代点:[1.0000311207482149, 1.0000594706577797, 0.999965823924486, 0.999928146607472], 共经历418次迭代
DFP 最终迭代点:[1. 1. 1. 1.], 共经历53次迭代
BFGS 最终迭代点:[0.99999614 0.99999229 0.99999844 0.99999693], 共经历60次迭代
BB方法
在拟 Newton 法中,我们寻找对称矩阵 B k + 1 B_{k+1} Bk+1? 使得 B k + 1 s k = y k . B_{k+1}s_k=y_k. Bk+1?sk?=yk?. Barzilai 和 Borwein 提出:取 B k + 1 = α ? 1 I B_{k+1}=\alpha^{-1}I Bk+1?=α?1I.然而,这样的选取一般不能满足 B k + 1 s k = y k B_{k+1}s_k=y_k Bk+1?sk?=yk?.因此,BB 方法将该等式条件改为
α k + 1 : = argmin ? α > 0 ∥ α ? 1 s k ? y k ∥ 2 . \alpha_{k+1}:=\underset{\alpha>0}{\operatorname*{argmin}}\|\alpha^{-1}s_k-y_k\|_2. αk+1?:=α>0argmin?∥α?1sk??yk?∥2?.解之得 α k + 1 = s k T s k / ( s k T y k ) \alpha_{k+1}=s_k^Ts_k/(s_k^Ty_k) αk+1?=skT?sk?/(skT?yk?).类似于拟 Newton 法使用 d k + 1 = ? B k + 1 ? 1 ? f ( x k + 1 ) d_{k+1}=-B_{k+1}^{-1}\nabla f(x_{k+1}) dk+1?=?Bk+1?1??f(xk+1?) 为搜索方向,BB 算法采用
d k + 1 : = ( α k + 1 ? 1 I ) ? 1 ? f ( x k + 1 ) = α k + 1 ? f ( x k + 1 ) . d_{k+1}:=(\alpha_{k+1}^{-1}I)^{-1}\nabla f(x_{k+1})=\alpha_{k+1}\nabla f(x_{k+1}). dk+1?:=(αk+1?1?I)?1?f(xk+1?)=αk+1??f(xk+1?).
所以,BB 算法的搜索方向仍是负梯度方向. 由于上面已经考虑了步长,所以 BB 算法不再搜索步长. 这样我们得到如下的迭代公式 x k + 1 = x k ? α k ? f ( x k ) , α k = s k ? 1 T s k ? 1 s k ? 1 T y k ? 1 x_{k+1}=x_k-\alpha_k\nabla f(x_k),\quad\alpha_k=\frac{s_{k-1}^Ts_{k-1}}{s_{k-1}^Ty_{k-1}} xk+1?=xk??αk??f(xk?),αk?=sk?1T?yk?1?sk?1T?sk?1??类似地,我们将条件 H k + 1 y k = s k H_{k+1}y_k=s_k Hk+1?yk?=sk? 替换成
α k + 1 : = a r g m i n α > 0 ∥ α y k ? s k ∥ 2 . \alpha_{k+1}:=\mathop{\mathrm{argmin}}_{\alpha>0}\|\alpha y_k-s_k\|_2. αk+1?:=argminα>0?∥αyk??sk?∥2?.
解之得 α k + 1 = s k T y k / ( y k T y k ) \alpha_{k+1}=s_k^Ty_k/(y_k^Ty_k) αk+1?=skT?yk?/(ykT?yk?). 从而得到如下迭代公式
x
k
+
1
=
x
k
?
α
k
?
f
(
x
k
)
,
α
k
=
s
k
?
1
T
y
k
?
1
y
k
?
1
T
y
k
?
1
.
x_{k+1}=x_k-\alpha_k\nabla f(x_k),\quad\alpha_k=\frac{s_{k-1}^Ty_{k-1}}{y_{k-1}^Ty_{k-1}}.
xk+1?=xk??αk??f(xk?),αk?=yk?1T?yk?1?sk?1T?yk?1??.公式
x
k
+
1
=
x
k
?
α
k
?
f
(
x
k
)
,
α
k
=
s
k
?
1
T
s
k
?
1
s
k
?
1
T
y
k
?
1
x_{k+1}=x_k-\alpha_k\nabla f(x_k),\quad\alpha_k=\frac{s_{k-1}^Ts_{k-1}}{s_{k-1}^Ty_{k-1}}
xk+1?=xk??αk??f(xk?),αk?=sk?1T?yk?1?sk?1T?sk?1?? 和
x
k
+
1
=
x
k
?
α
k
?
f
(
x
k
)
,
α
k
=
s
k
?
1
T
y
k
?
1
y
k
?
1
T
y
k
?
1
x_{k+1}=x_k-\alpha_k\nabla f(x_k),\quad\alpha_k=\frac{s_{k-1}^Ty_{k-1}}{y_{k-1}^Ty_{k-1}}
xk+1?=xk??αk??f(xk?),αk?=yk?1T?yk?1?sk?1T?yk?1?? 分别称为 BB1 公式和 BB2 公式,为区别起见,分别将它们对应的步长
α
k
\alpha_k
αk? 记为
α
k
B
B
1
\alpha_k^\mathrm{BB1}
αkBB1? 和
α
k
B
B
2
\alpha_k^\mathrm{BB2}
αkBB2?,即
α
k
B
B
1
=
s
k
?
1
T
s
k
?
1
s
k
?
1
T
y
k
?
1
,
α
k
B
B
2
=
s
k
?
1
T
y
k
?
1
y
k
?
1
T
y
k
?
1
.
\alpha_{k}^{\mathrm{BB}1}=\frac{s_{k-1}^{T}s_{k-1}}{s_{k-1}^{T}y_{k-1}},\quad\alpha_{k}^{\mathrm{BB}2}=\frac{s_{k-1}^{T}y_{k-1}}{y_{k-1}^{T}y_{k-1}}.
αkBB1?=sk?1T?yk?1?sk?1T?sk?1??,αkBB2?=yk?1T?yk?1?sk?1T?yk?1??.特别若目标函数为
f
(
x
)
=
1
2
x
T
A
x
+
b
T
x
f(x)=\frac12x^TAx+b^Tx
f(x)=21?xTAx+bTx, 其中
A
A
A 为对称正定矩阵,
b
∈
R
n
b\in\mathbb{R}^n
b∈Rn, 计算可得
s
k
?
1
=
?
α
k
?
1
?
f
(
x
k
?
1
)
,
y
k
?
1
=
A
s
k
?
1
=
?
α
k
?
1
A
?
f
(
x
k
?
1
)
s_{k-1}=-\alpha_{k-1}\nabla f(x_{k-1}),\quad y_{k-1}=As_{k-1}=-\alpha_{k-1}A\nabla f(x_{k-1})
sk?1?=?αk?1??f(xk?1?),yk?1?=Ask?1?=?αk?1?A?f(xk?1?)从而
α
k
BB
1
=
?
f
(
x
k
?
1
)
T
?
f
(
x
k
?
1
)
?
f
(
x
k
?
1
)
T
A
?
f
(
x
k
?
1
)
,
α
k
BB
2
=
?
f
(
x
k
?
1
)
T
A
?
f
(
x
k
?
1
)
?
f
(
x
k
?
1
)
T
A
2
?
f
(
x
k
?
1
)
,
\alpha_{k}^{\text{BB}1}=\frac{\nabla f(x_{k-1})^T\nabla f(x_{k-1})}{\nabla f(x_{k-1})^TA\nabla f(x_{k-1})},\quad\alpha_{k}^{\text{BB}2}=\frac{\nabla f(x_{k-1})^TA\nabla f(x_{k-1})}{\nabla f(x_{k-1})^TA^2\nabla f(x_{k-1})},
αkBB1?=?f(xk?1?)TA?f(xk?1?)?f(xk?1?)T?f(xk?1?)?,αkBB2?=?f(xk?1?)TA2?f(xk?1?)?f(xk?1?)TA?f(xk?1?)?,易见,此时有
α
k
B
B
1
=
α
k
S
D
,
?
α
k
B
B
2
=
α
k
M
D
\alpha_k^\mathrm{BB1}=\alpha_k^\mathrm{SD},\:\alpha_k^\mathrm{BB2}=\alpha_k^\mathrm{MD}
αkBB1?=αkSD?,αkBB2?=αkMD?, 其中,
α
k
S
D
\alpha_k^\mathrm{SD}
αkSD? 表示最速下降法之精确搜索的步长
α
k
M
D
\alpha_k^\mathrm{MD}
αkMD? 称为最小梯度法的步长,因为它满足
α
k
M
D
=
argmin
?
α
>
0
∥
?
f
(
x
k
?
α
?
f
(
x
k
)
)
∥
2
=
?
f
(
x
k
)
T
A
?
f
(
x
k
)
?
f
(
x
k
)
T
A
2
?
f
(
x
k
)
.
\alpha_k^{\mathrm{MD}}=\underset{\alpha>0}{\operatorname*{argmin}}\|\nabla f(x_k-\alpha\nabla f(x_k))\|_2=\frac{\nabla f(x_k)^TA\nabla f(x_k)}{\nabla f(x_k)^TA^2\nabla f(x_k)}.
αkMD?=α>0argmin?∥?f(xk??α?f(xk?))∥2?=?f(xk?)TA2?f(xk?)?f(xk?)TA?f(xk?)?.
上面这些证明我就贴在这水个字数,我是看不懂的- -
Reference
本笔记的代码部分来源于下篇文章:
最优化方法复习笔记(四)拟牛顿法与SR1,DFP,BFGS三种拟牛顿算法的推导与代码实现
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!