6.【自动驾驶与机器人中的SLAM技术】鲁邦核函数的含义和应用

1. 给ICP和NDT配准添加柯西核函数

鲁邦核函数的意义：

在实际优化过程中，很可能会出现误匹配的项，这些误匹配的项被算法当做要降低的误差对待，由于误匹配的“误差”会很大，降低它能够明显使总的误差降低，但是显然这些项不应该被当做误差项对待，因为他会抹平其它正确边的影响，使得优化算法专注于调整一个错误的值。鲁邦核函数正好可以解决这个问题。核函数保证每条边的误差不会大的没边而掩盖其它的边。具体的方式就是，把原先误差的二范数度量替换成一个增长没那么快的函数，同时保证自己的光滑性质。

$下面是柯西核函数在最小二乘问题上的应用$: 此处可以看一下这篇博文，里面讲了非线性最小二乘问题以及核函数。


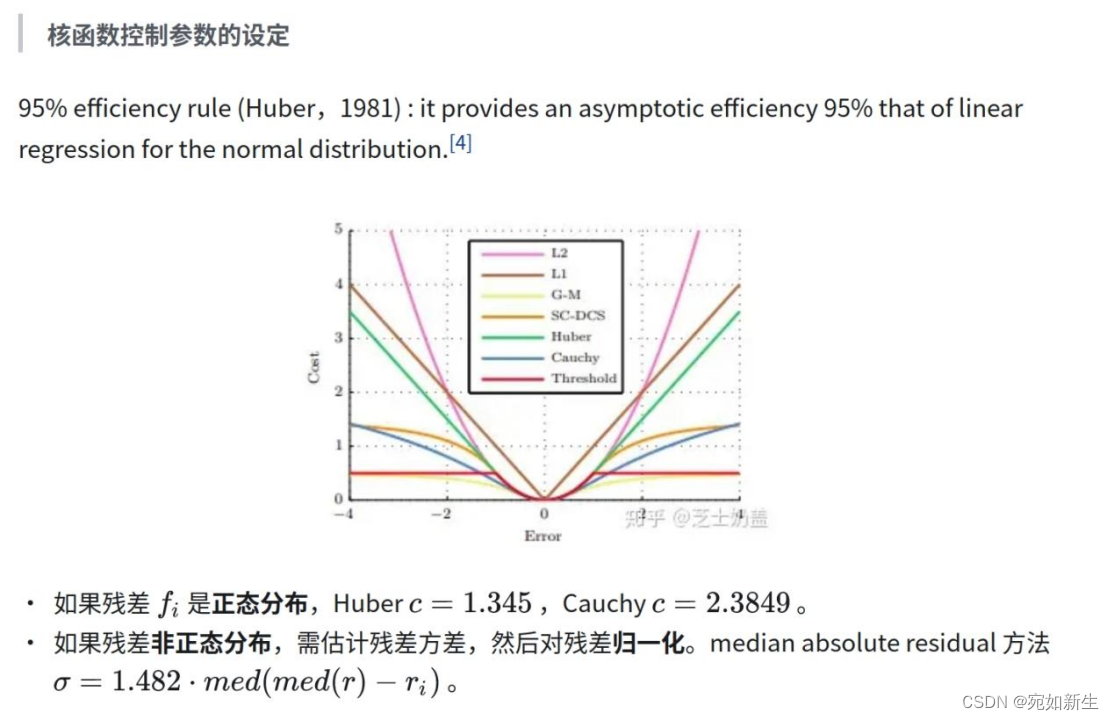
g2o中柯西函数的实现：

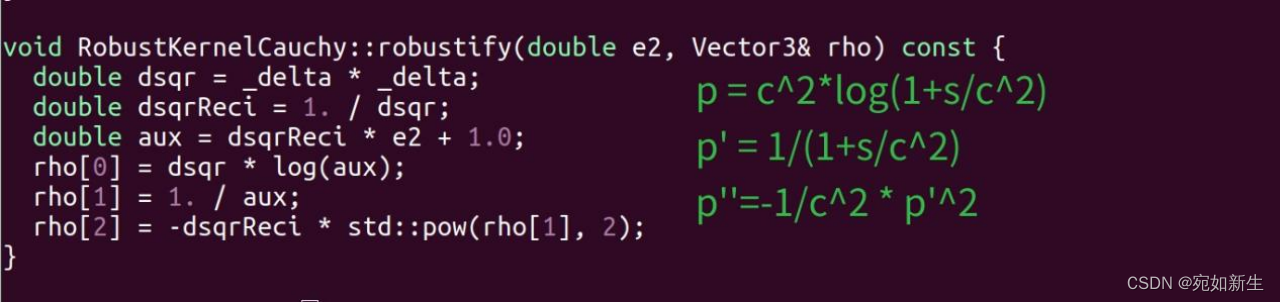
可以去看看g2o是如何使用核函数进行优化的源码，通过看g2o源码对核函数的实现可以粗略总结出，要做的工作分两部分，
1.实现柯西核函数（控制阈值c选择, 残差在正态分布情况下选择2.3849，非正态分布下没有一定值，这里直接设置为1.0）；
2. 根据上面的公式推导拼正规方程。

1.1 代码实现

point2point:

auto H_and_err = std::accumulate(
            index.begin(), index.end(), std::pair<Mat6d, Vec6d>(Mat6d::Zero(), Vec6d::Zero()),
            [&jacobians, &errors, &effect_pts, &total_res, &effective_num](const std::pair<Mat6d, Vec6d>& pre,
                                                                           int idx) -> std::pair<Mat6d, Vec6d> {
                if (!effect_pts[idx]) {
                    return pre;
                } else {
                    double e2 = errors[idx].dot(errors[idx]);
                    total_res += e2;
                    effective_num++;

                    // Cauchy 鲁棒核函数
                    double delta =  1.0;                    // 控制阈值设置为1.0
                    double delta2 = delta * delta;
                    double delta2_inv = 1.0 / delta2;
                    double aux = delta2_inv * e2 + 1.0;

                    Vec3d rho;
                    rho[0] = delta2  * log(aux);            // Cauchy核函数
                    rho[1] = 1.0 / aux;                     // Cauchy核函数的一阶导数
                    rho[2] = -delta2_inv * pow(rho[1],2);   // Cauchy核函数的二阶导数

                    Mat3d weighted_infos = rho[1] * Mat3d::Identity() + 2 * rho[2] * errors[idx] * errors[idx].transpose();

                    return std::pair<Mat6d, Vec6d>(pre.first + jacobians[idx].transpose() * weighted_infos * jacobians[idx],
                                                   pre.second - rho[1] * jacobians[idx].transpose() * errors[idx]);
                }
            });

几种配准方法代码大同小异这里只贴出point2point的吧。其他ICP类型和NDT可以遵照point2point实现。以下是四种配准方法加了柯西核函数之后的表现。

2. 将第1部分的robust loss引入IncNDTLO和LooselyLIO，给出实现和运行效果

这里在看LooselyLIO代码时，发现其调用的方法就是IncNDTLO，而IncNDTLO在AddCloud中的配准方法就是IncNdt3d。只需要修改src/ch7/ndt_inc.cc文件中的AlignNdt()函数即可。修改和第一题中的代码一致。
运行效果：（加核函数前后表现差异不大）

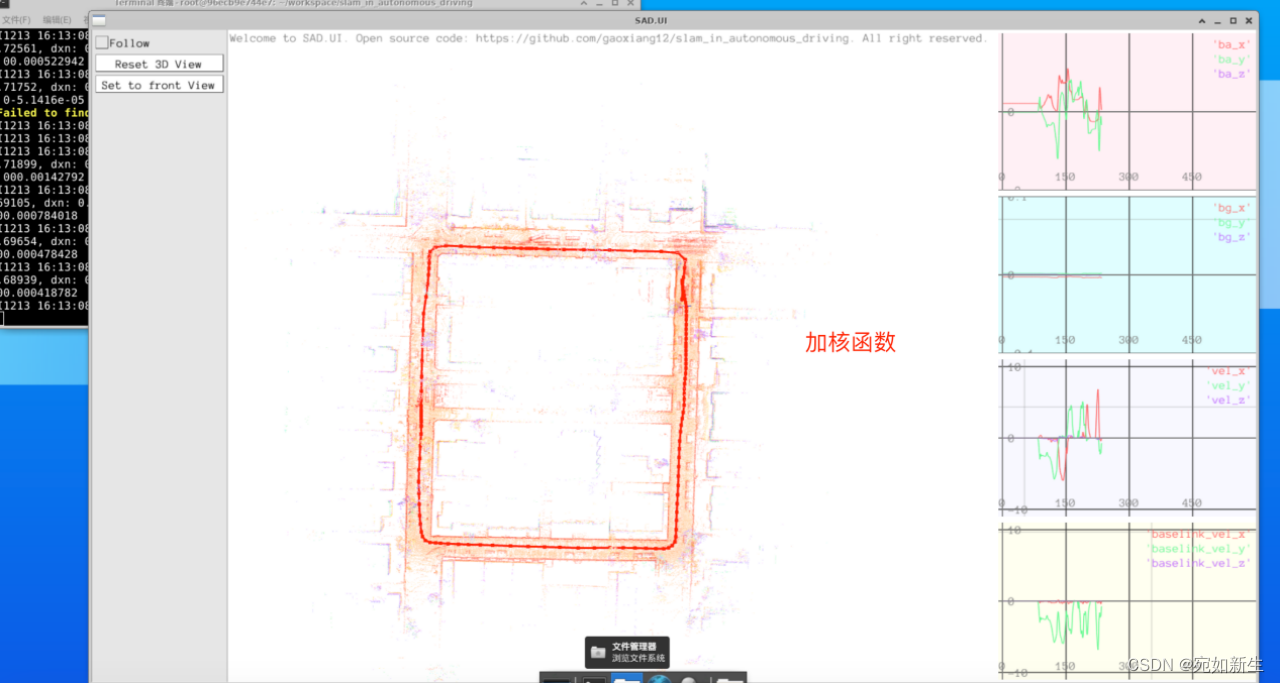
3. 从概率层面解释NDT残差和协方差矩阵的关系，说明为什么NDT协方差矩阵可以用于最小二乘

4. 为LOAM like LO设计一个地面点云提取流程，并单独为这些点使用点面ICP

论文参考：Fast segmentation of 3D point clouds: A paradigm on LiDAR data for autonomous vehicle applications
地面提取思路：一帧3D点云包含的点数众多，我们要提取地面，可以只选出接近地面的一些点拿来拟合平面，可以降低大量计算。

论文中的LPR算法流程如下：（种子点可以理解为近地点，不过种子点的提取要求雷达与地面大体垂直，不然无法按照论文中思路提取出种子点，因为近地点提取原理就是对激光点云排序，选Z值小的点，如果激光雷达正对着地面，此方法失效。–当然大多数雷达不会这么做。）

4.1 代码实现

void FeatureExtraction::ExtractGroundPlane(CloudPtr point_input_xyz, CloudPtr pc_ground)
{
    int lpr_max_iters = 100; // lpr算法 最大迭代次数
    double lpr_least_gpoints_rate = 0.3; // 用于计算近地点阈值的一个比率，按照整帧点云点数来确定点数计算近地点阈值，这个阈值用来提取种子点
    double lpr_fit_dist_thre = 0.05; // 到平面距离小于此阈值的点就属于平面点
    // find the lpr plane
    CloudPtr sort_cloud = point_input_xyz; 
    // 对点云按Z值排序
    std::sort(
        sort_cloud->points.begin(), sort_cloud->points.end(),
        [&](const PointType& p1, const PointType& p2) { return p1.z < p2.z; });

    // extract init ground seeds
    double lpr_avg_height = 0;
    size_t lpr_num = static_cast<size_t>(lpr_least_gpoints_rate *
                                         sort_cloud->points.size());
    for (size_t i = 0; i < lpr_num; i++) 
    {
        lpr_avg_height += sort_cloud->points[i].z;
    }
    lpr_avg_height /= lpr_num;

    CloudPtr pc_for_ground(new sad::PointCloudType);

    for (size_t i = 0; i < sort_cloud->points.size(); i++) 
    {
        if (sort_cloud->points[i].z <= lpr_avg_height) 
        {
            pc_for_ground->points.emplace_back(sort_cloud->points[i]);
        } else 
        {
            break;
        }
    }

    // ransac fitting iteratively
    PlaneParam plane(Eigen::Vector3d::Zero(), 0);
    PlaneParam last_pp(Eigen::Vector3d::Zero(), 0);
    
    for (int iter_cnt = 0; iter_cnt < lpr_max_iters; iter_cnt++) 
    {
        // fitting plane
        {
            // calculate the mean and cov
            std::vector<Eigen::Vector3d> points;
            Eigen::Vector3d mean(0.0, 0.0, 0.0);
            for (size_t j = 0; j < pc_for_ground->points.size(); j++) 
            {
                PointType point = pc_for_ground->points[j];
                Eigen::Vector3d temp(point.x, point.y, point.z);
                mean += temp;
                points.emplace_back(temp);
            }
            mean = mean / pc_for_ground->points.size();
            Eigen::Matrix3d cov = Eigen::Matrix3d::Zero();
            for (size_t j = 0; j < points.size(); j++) 
            {
                Eigen::Vector3d temp = points[j] - mean;
                cov = cov + temp * temp.transpose();
            }
            // svd
            Eigen::JacobiSVD<Eigen::MatrixXd> svd(
                cov, Eigen::DecompositionOptions::ComputeFullU);
            plane.normal = (svd.matrixU().col(2));
            plane.intercept = -(plane.normal.transpose() * mean)(0, 0);
        }

        pc_ground->points.clear();
        for (size_t j = 0; j < pc_for_ground->points.size(); j++) 
        {
            PointType point = pc_for_ground->points[j];
            double point_to_plane_dis = std::fabs(plane.normal(0) * point.x + plane.normal(1) * point.y +
                plane.normal(2) * point.z + plane.intercept);

            if (point_to_plane_dis <= lpr_fit_dist_thre) 
            {
                pc_ground->points.emplace_back(point);
            } 
        }
        // convergence check
        Eigen::Vector3d dlt_norm = plane.normal - last_pp.normal;
        double dlt_intcpt = plane.intercept - last_pp.intercept;
        if (dlt_norm.norm() < 0.001 && dlt_intcpt < 0.01 && iter_cnt > lpr_max_iters / 2)
        {
            LOG(INFO) << "ExtractGroundPlane success!!!";
            break;
        }
        last_pp = plane;
    }
    return;
}

$地面提取效果：$

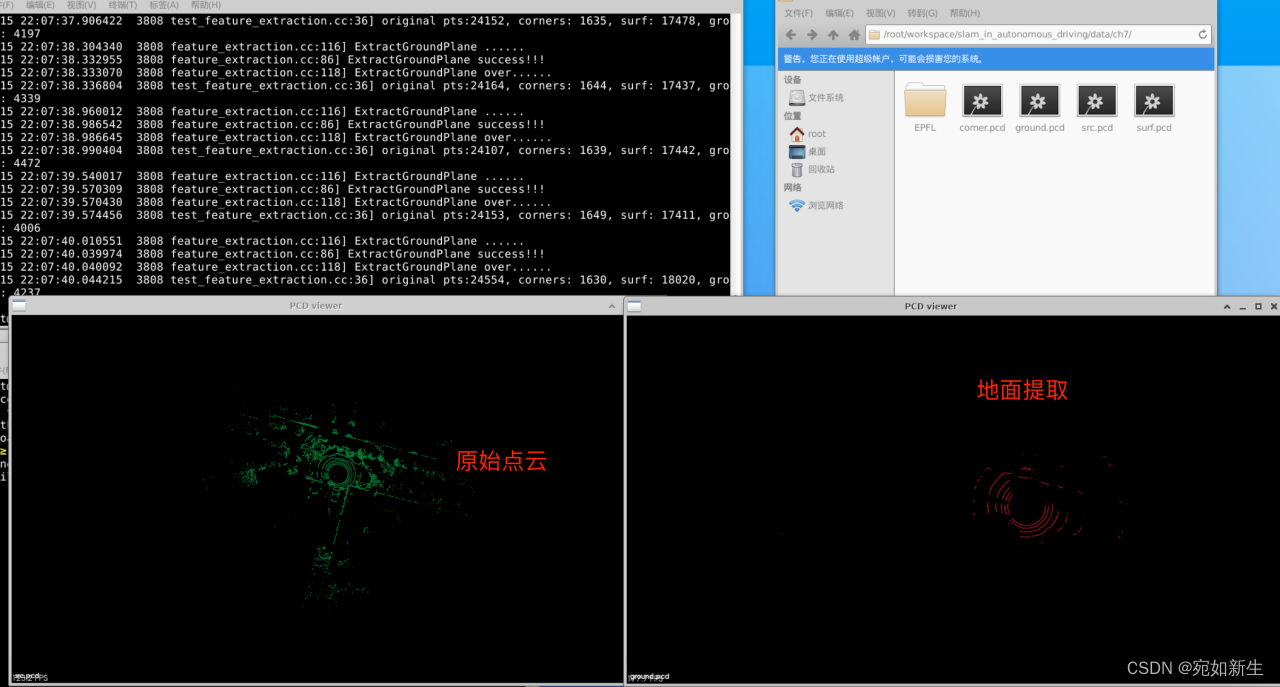
4.2 对地面点进行ICP

相关变量声明：


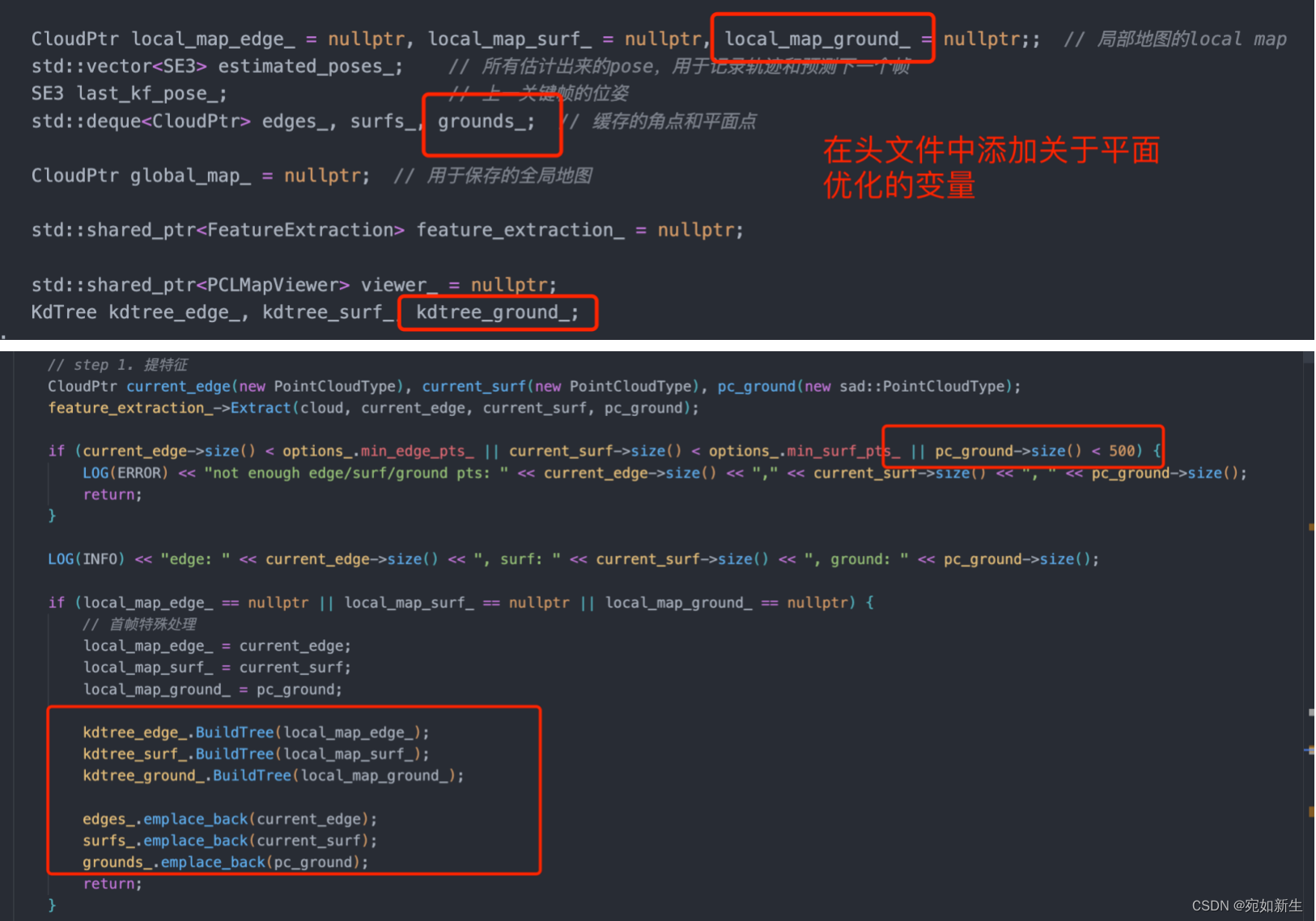
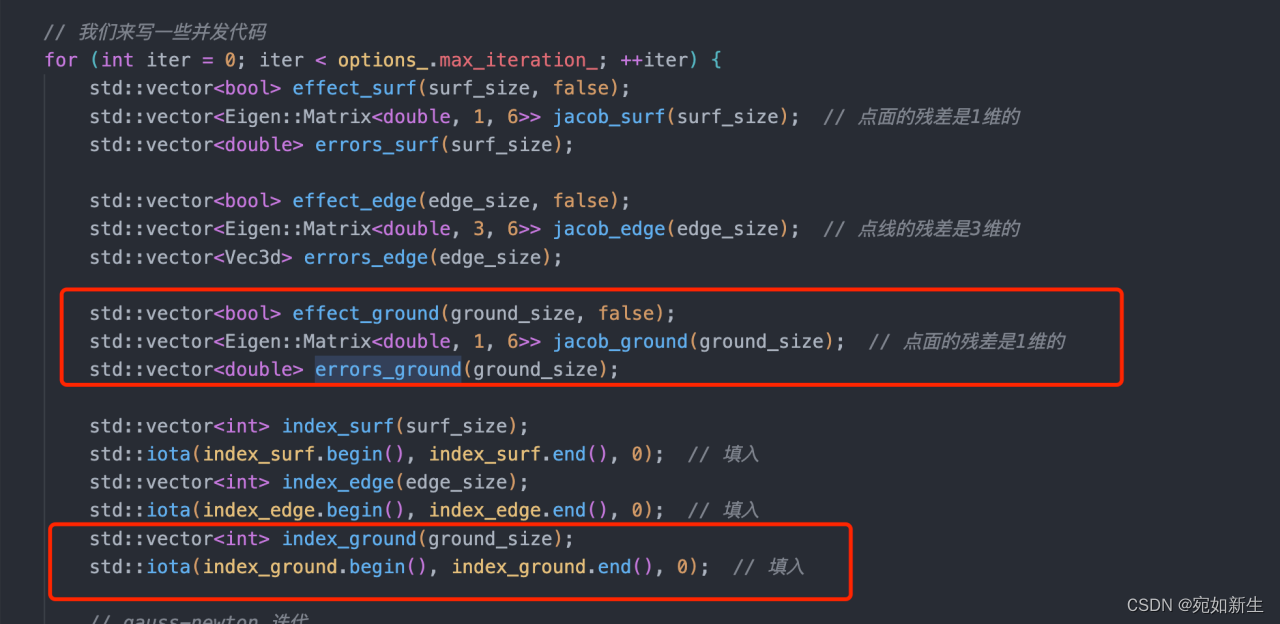
核心代码实现：

if (options_.use_ground_points_) 
        {
            std::for_each(std::execution::par_unseq, index_ground.begin(), index_ground.end(), [&](int idx) 
            {
                Vec3d q = ToVec3d(ground->points[idx]);
                Vec3d qs = pose * q;

                // 检查最近邻
                std::vector<int> nn_indices;

                kdtree_ground_.GetClosestPoint(ToPointType(qs), nn_indices, 5);
                effect_ground[idx] = false;

                if (nn_indices.size() == 5) 
                {
                    std::vector<Vec3d> nn_eigen;
                    for (auto& n : nn_indices) 
                        nn_eigen.emplace_back(ToVec3d(local_map_ground_->points[n]));
                    // 点面残差
                    Vec4d n;
                    if (!math::FitPlane(nn_eigen, n)) 
                        return;

                    double dis = n.head<3>().dot(qs) + n[3];
                    if (fabs(dis) > options_.max_plane_distance_) 
                        return;

                    effect_ground[idx] = true;
                    
                    // build residual
                    Eigen::Matrix<double, 1, 6> J;
                    J.block<1, 3>(0, 0) = -n.head<3>().transpose() * pose.so3().matrix() * SO3::hat(q);
                    J.block<1, 3>(0, 3) = n.head<3>().transpose();

                    jacob_ground[idx] = J;
                    errors_ground[idx] = dis;
                }
            });
        }
        
        for (const auto& idx : index_ground) 
        {
             if (effect_ground[idx]) 
             {
                 H += jacob_ground[idx].transpose() * jacob_ground[idx];
                 err += -jacob_ground[idx].transpose() * errors_ground[idx];
                 effective_num++;
                 total_res += errors_ground[idx] * errors_ground[idx];
             }
         }

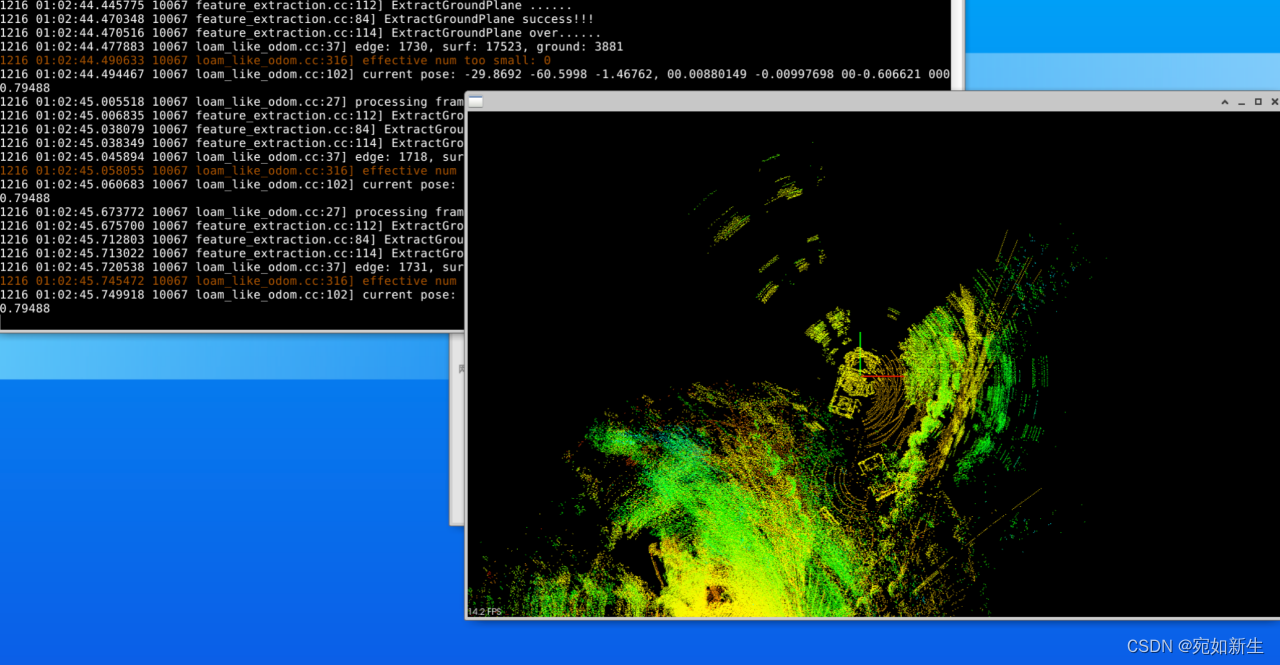
实现效果：
①仅使用提取的地面点来进行定位：（可以看到效果非常不好，地面提取算法可能还需要优化，也有可能本身只使用地面点来配准就效果很差，这个可以继续尝试优化。）

②使用角点和地面点一起定位：（明显角点的匹配很好的把地面匹配的结果矫正了，但是一开始部分还是不行。）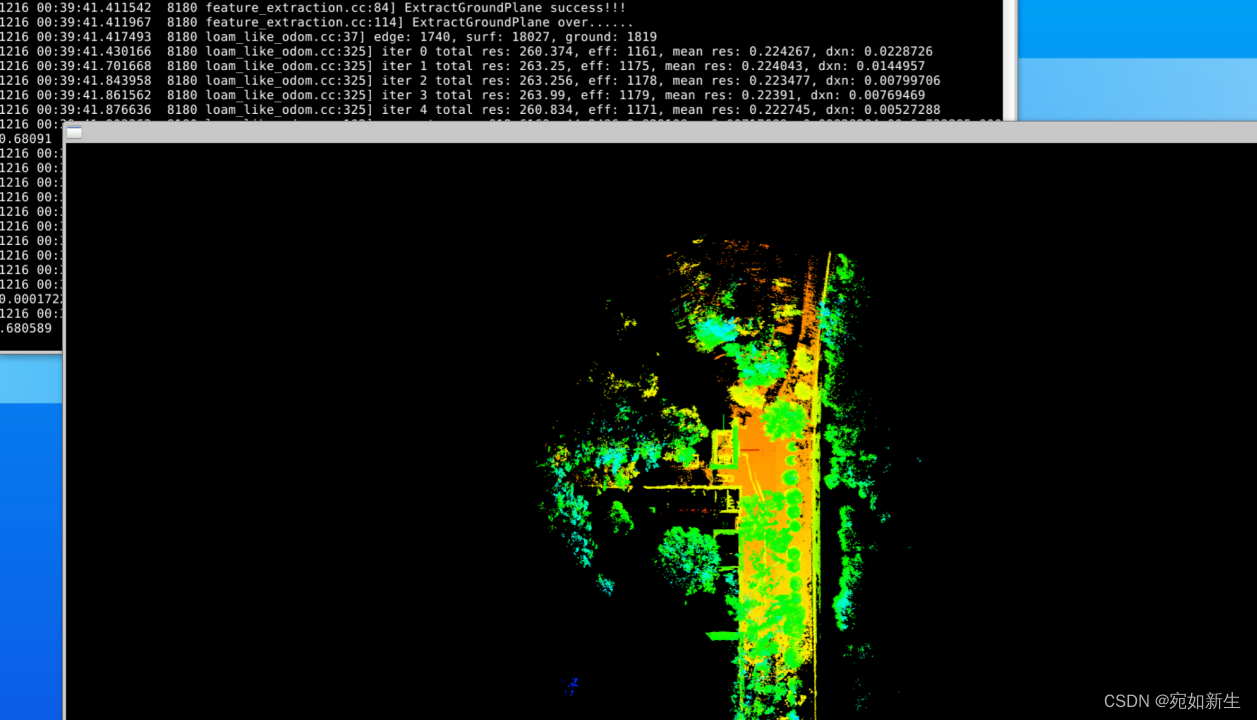

5. 也欢迎大家来我的微信公众号–过千帆，来读书，提高我们的认知。