【数据挖掘 | 关联规则】FP-grow算法详解(附详细代码、案例实战、学习资源)
!

🤵?♂? 个人主页: @AI_magician
📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。
👨?💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!🐱?🏍
🙋?♂?声明:本人目前大学就读于大二,研究兴趣方向人工智能&硬件(虽然硬件还没开始玩,但一直很感兴趣!希望大佬带带)

摘要: 本系列旨在普及那些深度学习路上必经的核心概念,文章内容都是博主用心学习收集所写,欢迎大家三联支持!本系列会一直更新,核心概念系列会一直更新!欢迎大家订阅
该文章收录专栏
[?— 《深入解析机器学习:从原理到应用的全面指南》 —?]
@toc
FP-Growth算法
Apriori算法需要多次扫描数据,I/O是很大的瓶颈。为了解决这个问题,FP-Growth(Frequent Pattern Growth)通过构建FP树(Frequent Pattern Tree)来避免生成候选项集,从而减少了搜索空间,提高了算法的效率。无论多少数据,只需要扫描两次数据集,因此提高了算法运行的效率。
FP Tree算法引入了一些数据结构来临时存储数据。这个数据结构包括三部分,如下图所示:

1. 项头表(线性结构):里面记录了所有的1项频繁集出现的次数,按照次数降序排列。比如上图中B在所有10组数据中出现了8次,因此排在第一位。
- FP Tree(树结构):它将我们的原始数据集映射到了内存中的一颗FP树。
- 节点链表:所有项头表里的1项频繁集都是一个节点链表的头,它依次指向FP树中该1项频繁集出现的位置。这样做主要是方便项头表和FP Tree之间的联系,以查找和更新。
算法步骤:
-
构建项头表(Header Table):遍历数据集,统计每个项的支持度,删除支持度低于阈值的项,最后按照支持度降序排序。构建一个项头表,每个项头表项包含项的名称、支持度计数和指向该项在FP树中第一个节点的指针。在实际操作中需要扫描两次数据,第一次用于统计项支持度操作,第二次扫描用于删除支持度低于阈值中事务的项。(其中之所排序是因为在FP树的建立时,可以尽可能的共用祖先节点)
-
构建FP树:遍历数据集,读取每一条事务依次构建FP树。对于每个事务中的项,从根节点开始,如果该项在当前节点的子节点中存在,则增加子节点的支持度计数;否则,创建一个新的子节点,并更新项头表中该项的链表。最后构建得到的树称为FP树。
-
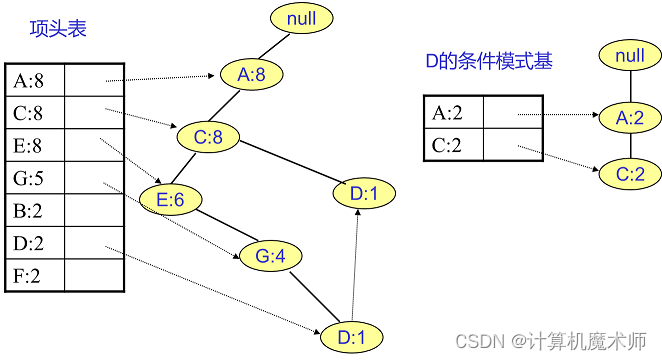
构建条件模式基:对于每个项头表中的项,从项头表链表的末尾开始,递归遍历该项的链表,生成以该项为后缀路径的条件模式基。每个条件模式基包含路径中除了当前项的其他项以及对应的支持度计数。
D的条件模式基如下图。将所有的祖先节点计数设置为叶子节点的计数,即变成{A:2, C:2,E:1 G:1,D:1, D:1},此时E节点和G节点由于在条件模式基里面的支持度低于阈值,被我们删除,最终在去除低支持度节点并不包括叶子节点后D的条件模式基为{A:2, C:2}。
-
递归挖掘FP树:对于每个项头表中的项,将它与条件模式基组合,形成新的频繁项集。如果条件模式基非空,则以条件模式基为输入递归调用FP树构建和挖掘过程。
在上一步得到条件模式基后,结合得到 D的频繁2项集为{A:2,D:2}, {C:2,D:2}。递归合并二项集,得到频繁三项集为{A:2,C:2,D:2}。D对应的最大的频繁项集为频繁3项集。
FP Tree算法改进了Apriori算法的I/O瓶颈,巧妙的利用了树结构,参考BIRCH聚类,BIRCH聚类也是巧妙的利用了树结构来提高算法运行速度。利用内存数据结构以空间换时间是常用的提高算法运行时间瓶颈的办法。
在实践中,FP Tree算法是可以用于生产环境的关联算法,而Apriori算法则做为先驱,起着关联算法指明灯的作用。除了FP Tree,像GSP,CBA之类的算法都是Apriori派系的。
经典案例和代码实现:
以下是一个使用Python的mlxtend库实现FP-Growth算法的示例代码:
from mlxtend.frequent_patterns import fpgrowth
from mlxtend.preprocessing import TransactionEncoder
import pandas as pd
# 创建示例数据集
dataset = [['Milk', 'Eggs', 'Bread'],
['Milk', 'Butter'],
['Cheese', 'Bread', 'Butter'],
['Milk', 'Eggs', 'Bread', 'Butter'],
['Cheese', 'Bread', 'Butter']]
# 使用TransactionEncoder将数据集转换为布尔矩阵
te = TransactionEncoder()
te_ary = te.fit(dataset).transform(dataset)
df = pd.DataFrame(te_ary, columns=te.columns_)
# 使用fpgrowth函数查找频繁项集
frequent_itemsets = fpgrowth(df, min_support=0.2, use_colnames=True)
print(frequent_itemsets)
这里使用了mlxtend库中的fpgrowth函数来执行FP-Growth算法。首先,将事务数据集转换为布尔矩阵表示,然后调用fpgrowth函数来寻找指定最小支持度阈值的频繁项集。
另外,如果你想使用自己实现的FP-Growth算法,可以参考相关的开源实现和算法细节。以下是一些学习资源,可以帮助你更深入地了解FP-Growth算法:
- Han, J., Pei, J., & Yin, Y. (2000). Mining frequent patterns without candidate generation. In Proceedings of the 2000 ACM SIGMOD international conference on Management of data (pp. 1-12).
- Agrawal, R., Imieliński, T., & Swami, A. (1993). Mining association rules between sets of items in large databases. ACM SIGMOD Record, 22(2), 207-216.
- mlxtend documentation: https://rasbt.github.io/mlxtend/
- Python implementation of FP-Growth algorithm: https://github.com/evandempsey/fp-growth
参考文章:
https://www.cnblogs.com/pinard/p/6307064.html

🤞到这里,如果还有什么疑问🤞
🎩欢迎私信博主问题哦,博主会尽自己能力为你解答疑惑的!🎩
🥳如果对你有帮助,你的赞是对博主最大的支持!!🥳
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!