计算机组成与体系结构(6分)
内容概述

数据的表示
进制转换
R 进制转十进制使用按权展开法,其具体操作方式为:将 R 进制数的每一位数值用 Rk 形示,即幂的底数是 R ,指数为 k , k 与该位和小数点之间的距离有关。当该位位于小数点左边, k 值是该位和小数点之间数码的个数,而当该位位于小数点右边, k 值是负值,其绝对值是该位和小数点之间数码的个数加1
二进制转十进制
10100.01
=
1
×
2
4
+
1
×
2
2
+
1
×
2
?
2
10100.01=1\times2^4+1\times2^2+1\times2-^2
10100.01=1×24+1×22+1×2?2
七进制转十进制
604.01
=
4
×
7
0
+
6
×
7
2
+
1
×
7
?
2
604.01=4\times7^0+6\times7^2+1\times7-^2
604.01=4×70+6×72+1×7?2


数码
数据表示
| 数值1 | 数值-1 | 1-1 | |
|---|---|---|---|
| 原码 | 0000 0001 | 1000 0001 | 1000 0001 |
| 反码 | 0000 0001 | 1111 1110 | 1111 1111 |
| 补码 | 0000 0001 | 1111 1111 | 0000 0000 |
| 移码 | 1000 0001 | 0111 1111 | 0000 0000 |
定义
**原码:**原码就是符号位加上真值的绝对值,即用第一位表示符号,其余位表示值。
**反码:**正数的反码是其本身;负数的反码是在其原码的基础上,符号位不变,其余各个位取反。
**补码:**正数的补码就是其本身;负数的补码是在其原码的基础上,符号位不变,其余各位取反,最后+1。(也即在反码的基础上+1)
**移码:**移码在补码的基础上,符号位取反。
为了解决原码做减法的问题, 出现了反码。
于是补码的出现,解决了0的符号问题以及0的两个编码问题。
移码的出现就是为了解决数在数轴上表示的问题。
数据表示范围

因为补码的-0和0是同一数所以范围会少一个。
浮点数表示
N = M ? R e N=M*R^e N=M?Re
其中M称为尾数,e是指数,R为基数
计算机结构

CPU
运算器
-
累加寄存器(AC):专门存放算术或逻辑运算的一个操作数和运算结果的寄存器。能进行加,减,读出,移位,求补等操作。是运算器的主要部分。
-
程序状态寄存器(PSW):该部件用来存放两类信息,一类是体现当前指令执行结果的各种状态信息(条件码),如有无进位,有无溢出,结果正负,信息是否为零等;另一类是存放控制信息,如允许中断,跟踪标志等。
-
数据缓冲寄存器DR
-
状态条件寄存器PSW
控制器
-
程序计数器(PC):程序计数器中存放的是下一条指令的地址。由于多数情况下程序是顺序执行的,所以程序计数器设计成自动加一的装置。当出现转移指令时,就需重填程序计数器。
-
指令寄存器(IR):中央处理器正在执行的操作码表存放在这里,即当前正在执行的所有指令。
-
指令译码器:将操作码解码,告诉中央处理器该做什么。
-
时序部件
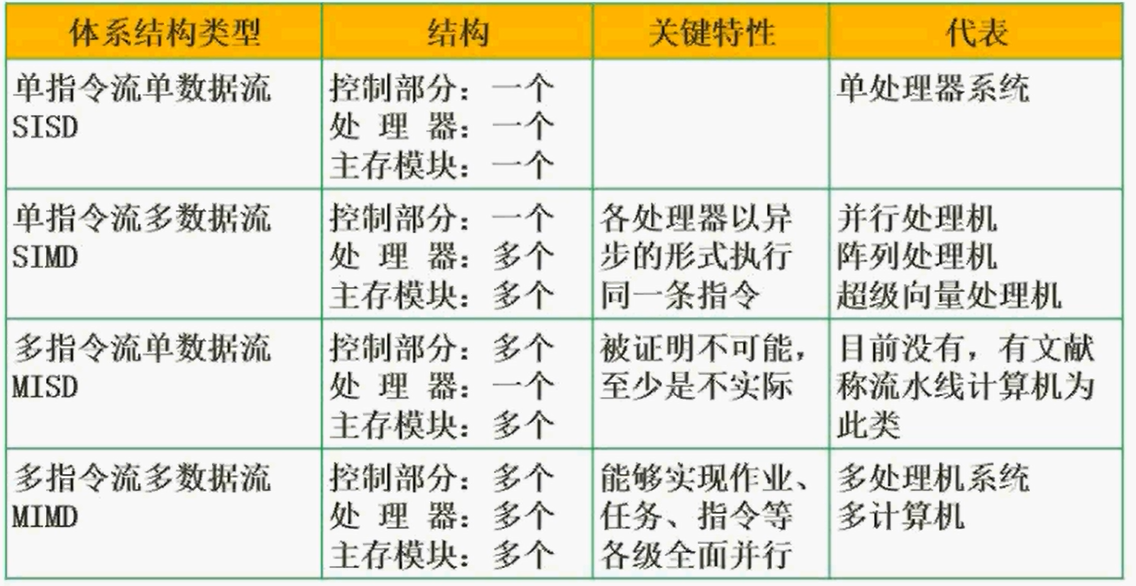
Flynn分类发
CISC与RISC
| 指令系统类型 | 指令 | 寻址方式 | 实现方式 | 其他 |
|---|---|---|---|---|
| CISC(复杂) | 数量多,使用频率差别大,可变长格式 | 支持多种 | 微程序控制技术 | 研制周期长 |
| RISC(精简) | 数量少,使用频率接近,定长格式,大部分为单周期指令,操作寄存器,只有Load/Store操作内存 | 支持方式少 | 增加了通用寄存器;硬布线逻辑控制为主;适合采用流水线 | 优化编译,有效支持高级语言 |
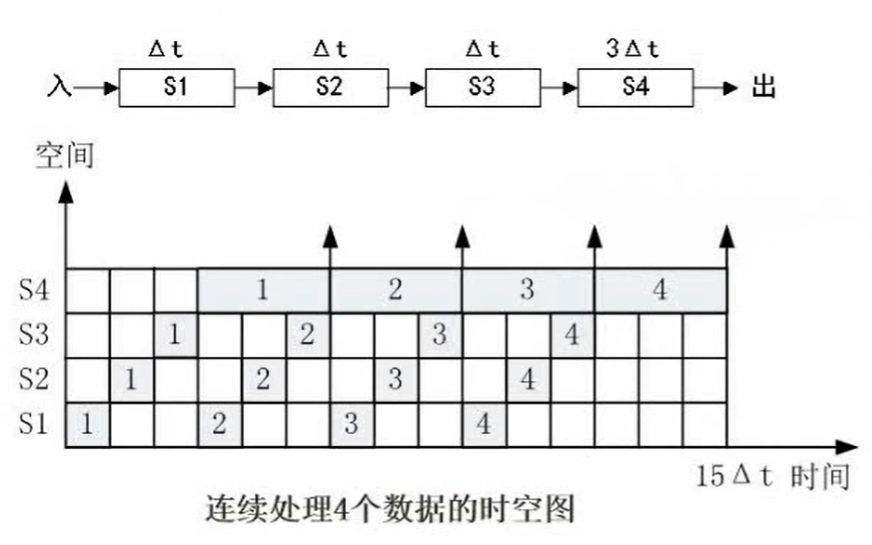
流水线技术
概念
流水线是指在程序执行时多条指令重叠进行操作的一种准并行处理实现技术。各种部件同时处理是针对不同指令而言的,它们可同时为多条指令的不同部分进行工作,以提高各部件的利用率和指令的平均执行速度。

周期和执行时间

考试时计算先按理论公式计算,如果理论公式没有答案就用实践公式计算
例:若指令流水线把一条指令分为取指、分折执行三部分,且三部分的时间分别是取指 2ns ,分折 2ns ,执行 lns 。那么,流水线周期是多少? 100 条指令全部执行完毕需要的时间是多少?
周期为2ns,100条指令全部执行完毕需要203ns。
吞吐率
流水线的吞吐率( Though Put rate TP)是指在单位时间内流水线所完成的任务数量或输出的结果数量。计算流水线吞吐率的最基本的公式如下:
T P = 指令条数 流水执行时间 TP= \frac{指令条数}{流水执行时间} TP=流水执行时间指令条数?
根据上面列子计算: 100 203 \frac{100}{203} 203100?
流水线最大吞吐率:
T P m a x = lim ? y → ∞ N ( k + n ? 1 ) × Δ t = l Δ t TP_{max}=\lim_{y \to \infty}\frac{N}{(k+n-1)\times\Delta t}=\frac{l}{\Delta t} TPmax?=y→∞lim?(k+n?1)×ΔtN?=Δtl?
根据上面列子计算: 1 2 \frac{1}{2} 21?
加速比
完成同样一批任务,不使用流水线所用的时间与使用流水线所用的时间之比称为流水线的加速比。计算流水线加速比的基本公式如下:
S = 不使用流水线执行时间 使用流水线执行时间 S= \frac{不使用流水线执行时间}{使用流水线执行时间} S=使用流水线执行时间不使用流水线执行时间?
根据上面列子计算: 500 203 \frac{500}{203} 203500?
效率
流水线的效率是指流水线的设备利用率。在时空图上,流水线的效率定义为 n 个任务占用的时空区与 k 个流水段总的时空区之比。就算流水线效率的公式为:
E = n 个任务占用的时空区 k 个流水段的总时空区 = T 0 k T k E=\frac{n个任务占用的时空区}{k个流水段的总时空区}=\frac{T_0}{kT_k} E=k个流水段的总时空区n个任务占用的时空区?=kTk?T0??
效率为: 24 60 \frac{24}{60} 6024?
每一个工作段时间相同工作效率最高
存储系统

Cache
Cache 的功能:提高 c 数据输入输出的速率,突破冯.诺依曼瓶颈,即 CPU 与存储系统间数据传送带宽限制。在计算机的存储系统体系中, cache 是访问速度最快的层次。使用 cache 改善系统性能的依据是程序的局部性原理。
如果以h代表对Cache的访问命中率,
t
1
t_1
t1?表示Cache的周期时间,
t
2
t_2
t2?表示主存储周期时间,以读操作为例,使用“Cache+主存储器”的系统的平均周期为
t
3
t_3
t3?,则:
t
3
=
h
×
t
1
+
(
1
?
h
)
×
t
2
t3=h\times t1+(1-h)\times t_2
t3=h×t1+(1?h)×t2?
其中,(1-h)又称为失效率(未命中率)。
主存
主存分为随机存起RAM和只读存储器ROM

主存编址题目计算

地址单元的计算公式为: ( 大地址 + 1 ) ? 小地址 单位 \frac{(大地址+1)-小地址}{单位} 单位(大地址+1)?小地址?,注意单位如果是K则除的是 2 10 2^{10} 210
本题的答案为:(1)B,(2)A
磁盘

计算题目
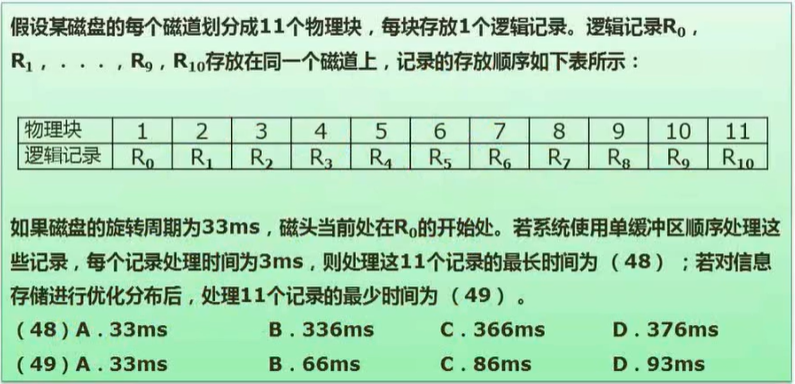
答案为:C,B
总线系统

可靠性
串联系统

并联系统

冗余模型
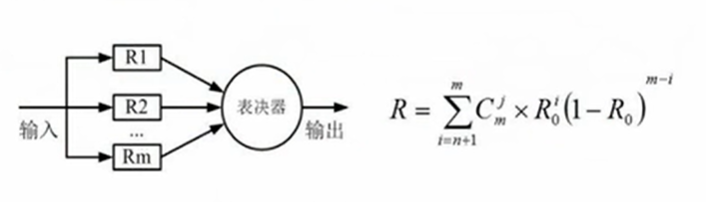
校验码
循环校验码CRC
循环冗余校验(Cyclic Redundancy Check, CRC)是一种根据网络数据包或计算机文件等数据产生简短固定位数校验码的一种信道编码技术,主要用来检测或校验数据传输或者保存后可能出现的错误。它是利用除法及余数的原理来作错误侦测的。
模二除法

模二除法性质
- 当最后余数的位数小于除数位数时,除法停止。
- 当被除数的位数小于除数位数时,则商数为0,被除数就是余数。
- 只要被除数或部分余数的位数与除数一样多,且最高位为1,不管其他位是什么数,皆可商1。
CRC编码的计算

- 通过多项式求出要除的值:11011。
- 给报文进行补位:多项式尾数减一个0,上面的题目中多项式是5位,我们要补4个0。
- 进行模二除法。
- 把补的0替换成计算出来地方余数,计算结果为:110010101010011。
海明校验码(难点)

求校验码位数
根据 m + k < = 2 k ? 1 m+k<=2^k-1 m+k<=2k?1公式确定检验码的位数,其中m原始信息码的位数,r校验码的位数。
① 此题中,信息码为 1011 ,共4位数,所以 k = 4
② 根据公式,将 k 值代入,解得符合表达式的值即为 r 的值,也就是校验码位数
此题中,可以算出 2^3 >= 4 + 3 + 1 ,所以 r = 3,校验码位数为3位
确认校验码位置
校验码的位置都是基于 2^n 来确定的,比如 2^0 = 1,2^1 = 2,2^2 = 4…
所以校验码的位置一般都是1、2、4、8…
① 海明码的长度 = 原始信息码 + 校验码
此题中,海明码长度 = 4 + 3 = 7位
② 建立一个从高位到低位的表格,表格列数即为海明码的长度
先填校验码,在本题中,校验码为3位,即占了1、2、4位,这里以r0、r1、r2来表示校验码
计算校验码
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 位数 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 信息位 | |||
| r 2 r_2 r2? | r 1 r_1 r1? | r 0 r_0 r0? | 校验位 | ||||
| I 4 I_4 I4? | I 3 I_3 I3? | I 2 I_2 I2? | r 2 r_2 r2? | I 1 I_1 I1? | r 1 r_1 r1? | r 0 r_0 r0? | 字母表示 |
I 4 I_4 I4?=7= 2 2 + 2 1 + 2 0 2^2+2^1+2^0 22+21+20
I 3 I_3 I3?=6= 2 2 + 2 1 2^2+2^1 22+21
I 2 I_2 I2?=5= 2 2 + 2 0 2^2+2^0 22+20
I 1 I_1 I1?=3= 2 1 + 2 0 2^1+2^0 21+20
校验位是根据相应的信息位进行异或运算得到的(如果信息吗是由校验码组成的,那么校验码就等于所有信息码的异或操作)
r 2 r_2 r2?= I 4 ? I 3 ? I 2 I_4\bigoplus I_3\bigoplus I_2 I4??I3??I2?= 1 ? 0 ? 1 1\bigoplus 0\bigoplus 1 1?0?1=0
r 1 r_1 r1?= I 4 ? I 3 ? I 1 I_4\bigoplus I_3\bigoplus I_1 I4??I3??I1?= 1 ? 0 ? 1 1\bigoplus 0\bigoplus 1 1?0?1=0
r 0 r_0 r0?= I 4 ? I 2 ? I 1 I_4\bigoplus I_2\bigoplus I_1 I4??I2??I1?= 1 ? 1 ? 1 1\bigoplus 1\bigoplus 1 1?1?1=1
海明码就是 1010101
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!