通配符匹配

给你一个输入字符串 (s) 和一个字符模式 (p) ，请你实现一个支持?'?'?和?'*'?匹配规则的通配符匹配：

• '?'?可以匹配任何单个字符。
• '*'?可以匹配任意字符序列（包括空字符序列）。

判定匹配成功的充要条件是：字符模式必须能够?完全匹配?输入字符串（而不是部分匹配）。

?题目分析：

?题目中给出'?'可以匹配任何单个字符，'*'可以匹配任何字符序列包括空字符。在里面*的不确定性最大，我们需要枚举所有的匹配情况。我们可以选择用动态规划来求解。

我们设一个bool类型的dp数组，初始值都是false。用dp[i][j]来表示s的前i个字符和p的前j个字符是否能匹配。。当(s[i]==s[j])的时候dp[i][j]=dp[i-1][j-1]。特殊情况下，p[j]为问号的时候，因为问号可以代表任何字符，所以dp[i][j]=dp[i-1][j-1]。当p[j]为星号的时候，它可以代表任意字符串，所以对s中任意字符都可以增加该字符使得原先匹配的两字符串在增加了s[i]的情况下再次匹配，或者是空串来得到s[i]和p[j-1]来匹配。得到公式

dp[i][j]=dp[i-1][j]或dp[i][j-1]。当其中有一个为true的时候为true。

总结公式得到：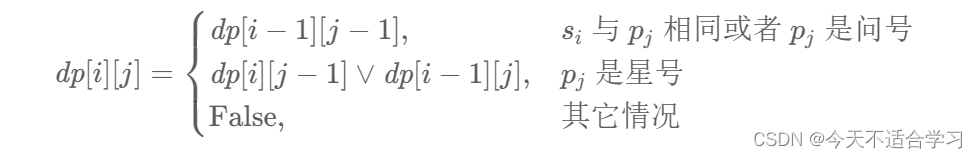

当i=0，j=0的时候两空字符串匹配dp[0][0]=true；?

当i=0的时候，也就是说s为空字符串，只有当p的前j个字符为星号的时候才可以表示空字符串，才能匹配，dp[0][j]=true；否则dp[0][j]=false。

当j=0，由于s没有办法表达空字符串，所以对于所有的dp[i][0]=false。

经过动态规划得到的dp[m][n]也就是说对于m长度的s和n长度的p可以匹配。

代码展现：

class Solution {
public:
    bool isMatch(string s, string p) {
        int m=s.size();
        int n=p.size();
        vector<vector<int>>dp(m+1,vector<int>(n+1));
        dp[0][0]=true;
        for(int i=1;i<=n;i++){
            if(p[i-1]=='*'){
                dp[0][i]=true;
            }
            else break;
        }
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(p[j-1]=='*')dp[i][j]=dp[i][j-1]|dp[i-1][j];
                else if(p[j-1]=='?'||s[i-1]==p[j-1])
                    dp[i][j]=dp[i-1][j-1];
            }
        }
        return dp[m][n];
    }
};

代码分析：

值得注意的是，dp从（1，1）开始遍历，而字符串从0开始，dp[i][j]对应的也就是s[i-1]和p[j-1]。

先用m，n表示s，p的长度。对dp状态方程赋值。

再根据公式对dp状态方程求解。

最后得到的dp[m][n]就是解。

复杂度：

时间复杂度：O(mn)

空间复杂度：O(mn)