Math-Ug-1a-Pasw-001-实数,幂,不等式
实数
实数:用于算术和测量的普通的数。
实 = real,existing in fact and not imaginary,实际存在的。
arithmetic,calculations involving adding and multiplying, etc. numbers,数加数,数乘数。
measure,to discover the exact size or amount of something,量尺寸或长度。
与复数相对(原书是这么说的,但我觉得确切来说,是和复数中的虚数单元相对)。
复 = complex,involving a lot of different but related parts,复数由实数和虚数单位构成,符合字面意义——不同的部分,但互相关联。
虚 = imaginary,不用解释了,和上面real词义中的not imaginary相对。
根据不同的特征,实数又分几种:
- 整数:一整个的数
integer = whole number
whole,complete or not divided
又分为正数,负数和0 - 有理数:可以表示成
p
q
\frac{p}{q}
qp? 这种分数形式的数,其中
p
,
q
p,q
p,q 都是整数。
rational:based on reason
有理数包含所有有限小数或无限循环小数。
recurring:repeating itself for ever
注意整数是有理数的一种。 - 剩下的就是无理数。不能像有理数那样表示成分数形式;它们表示成无限不循环小数。
represent:to show or describe something or someone
尽管有无数个有理数,但有比这个无数还更无数的无理数,所以无理数到处存在。
比如边长是单位长度的正方形对角线长 2 \sqrt{2} 2? 是无理数。 π , e \pi, e π,e 也都是无理数。
从无理数的无限不循环小数中留下一定位数,剩下的舍去,得到一个有限小数,这就是无理数的近似。 - 符号
∞
\infin
∞,表示无限,会频繁出现和用到,但不能在代数中作为一个普通数使用。诸如
∞ / ∞ = 1 ∞ ? ∞ = 0 \infin/\infin=1 \\ \infin-\infin=0 ∞/∞=1∞?∞=0
这样的式子都是不对的。
举个例子,我们从无限个整数中,取走无限个奇数,那剩下无限个偶数,无限减无限还是无限,不是0。
注:有限小数和无限小数中,有限无限是形容词,finite和infinite,指小数点后位数多少;
符号无限,是名词,infinity,larger than any other number and can never be given an exact value.
幂
数的幂具有
a
x
a^x
ax 的形式。幂
x
x
x 叫做指数或者指数。
这两个指数分别是exponent和index。
这里假定你知道当x是正数或负数时,分别使用什么规则。并且知道x是分数时,如何与平方根,立方根互相转换。
指数法则
已知
a
,
b
a, b
a,b是任意正实数;
x
,
y
x, y
x,y是任意实数,有
- a x a y = a x + y a^xa^y = a^{x+y} axay=ax+y
- a 0 = 1 a^0=1 a0=1
- a ? x = 1 a x a^{-x}=\frac{1}{a^x} a?x=ax1?
- ( a x ) y = a x y (a^x)^y=a^{xy} (ax)y=axy
-
a
x
b
x
=
(
a
b
)
x
(
1.1
)
a^xb^x=(ab)^x\quad(1.1)
axbx=(ab)x(1.1)
根式默认都是正根,若是负根,要加负号。
对于所有指数,
a
>
0
a>0
a>0是必要条件,因为负数没有实数平方根。
如果
a
a
a是负数,那么
a
x
a^x
ax有时是实数,仅当
x
=
p
/
q
x=p/q
x=p/q是最简形式,且
q
q
q是奇数。比如
(
?
8
)
1
3
=
?
2
(-8)^{\frac{1}{3}}=-2
(?8)31?=?2 因为
(
?
2
)
3
=
?
8
(-2)^3=-8
(?2)3=?8
最简形式 = lowest terms
不等式
说不等之前,先来说什么是相等。
首先相等要和方程区分开来。
语句
x
2
+
2
x
+
1
=
0
x^2+2x+1=0
x2+2x+1=0是方程:只有在特定条件下为真;换句话说,
x
x
x取特定的值,等号两边才相等。
方程 = equations
而
x
2
+
2
x
y
+
y
2
=
(
x
+
y
)
2
s
i
n
2
A
+
c
o
s
2
A
=
1
x^2+2xy+y^2=(x+y)^2\\sin^2A+cos^2A=1
x2+2xy+y2=(x+y)2sin2A+cos2A=1
这些叫做等式,因为对于所有
x
,
y
,
A
x,y,A
x,y,A值,等号两边都相等。
所以有时为了区分,我们用
≡
\equiv
≡表示等式。
任何包含
?
,
>
\leqslant, >
?,>的式子叫不等式。
代数类比语言,也拥有自己的‘短语’,就像上面列出的等式,叫做表达式。
通常情况,我们把带等号和不等号的式子都统称为方程。
画一条直线,在线上标一个点O——叫做原点,然后从O开始标定一个刻度。O点右侧正刻度,左侧负刻度。想象这个直线向两侧无限延伸。这叫做数轴。
indicate:to show,point
scale:a set of numbers, amounts, etc., used to measure or compare the level of something
每个实数都能在数轴上标出。我们用x表示一个普通的数。
不等式符号有各自的意义:
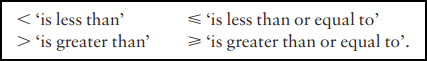
如果我们给两个数,那么在数轴上更靠右的数更大。
注意:
2
?
3
2\leqslant3
2?3也是成立的,因为只需要满足‘或’两种情况的其中一种即可。
数轴上的一小片,或一小段,叫做区间。
segment:one of the smaller groups or amounts that a larger group or amount can be divided into
interval:the space between two points,除此之外,a period between two events or times
区间两端叫做端点。
区间
2
?
x
?
3
2\leqslant x\leqslant3
2?x?3表示‘2和3之间,包括2和3的所有值x’。
区间
2
<
x
<
3
2<x<3
2<x<3表示‘2和3之间的所有值x,但不包括2和3’。
还有无限区间,有两种表示:
x
?
2
2
?
x
<
∞
x\geqslant 2\\ 2\leqslant x<\infin
x?22?x<∞
数的大小(尺寸)用
∣
x
∣
=
{
x
if?
x
?
0
?
x
if?
x
<
0
|x| = \begin{cases} x &\text{if } x\geqslant0 \\ -x &\text{if } x<0 \end{cases}
∣x∣={x?x?if?x?0if?x<0?
表示,叫做x的模数或绝对值。
modulus:the distance from zero of a number on a number line
我们可以用模数表示区间,比如,
∣
x
∣
<
2
|x|<2
∣x∣<2定义相同区间
?
2
<
x
<
2
-2<x<2
?2<x<2
自测题

# 在数轴上画出区间
NumberLinePlot[2<x<=4 &&Abs[x]<=3,x]
# 直接得出区间的重叠部分
Reduce[2<x<=4 &&Abs[x]<=3]
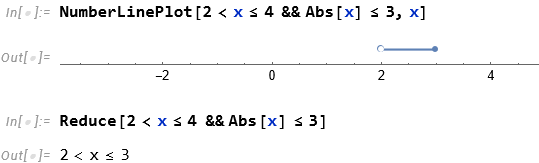
x可以取2,3之间的所有数,包括3不包括2。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!