Subgraph mining in a large graph: A review(2022 WIREs DMKD)
Subgraph mining in a large graph: A review ---- 《大图中的子图挖掘:回顾》
摘要
??大图通常用于对各种研究和应用领域中的复杂系统进行模拟和建模。由于其重要性,单个大图中的频繁子图挖掘(FSM)是一个至关重要的问题,最近它吸引了众多研究人员,并在研究和应用目的的各种任务中发挥了重要作用。FSM旨在找到大图中出现次数大于或等于给定频率阈值的所有子图。在最近的大多数应用中,底层图非常大,例如社交网络,因此基于单个大图的 FSM 算法得到了快速发展,但它们都具有 NP 难(非确定性多项式时间)复杂性和巨大的搜索空间,因此仍然需要大量的时间和内存来恢复和处理。在本文中,我们概述了 FSM 的问题、FSM 的重要阶段、FSM 的主要类别,并概述了许多现代应用算法。这包括许多实际应用,是未来许多研究的基本前提。
引言
??频繁模式(FP)挖掘是数据挖掘中最重要的任务之一。自从 1994 年 Apriori 算法被提出以来,许多高效挖掘 FP 的方法被开发出来,例如基于 FP-tree 的方法、Itemset-Tidset (IT)-基于树的方法、混合方法及其应用。频繁子图挖掘是数据挖掘(DM)最有趣的领域之一,并且是近年来吸引众多研究者的一个重要问题。FSM 在各种实际应用和任务中具有重要作用,例如决策支持系统、网络挖掘、地图模型分析信息检索系统、结构图聚类等等。在 DM 领域,闭项集挖掘已经发展了很长时间,并且一直是许多研究的焦点,但在图挖掘领域,封闭频繁子图挖掘是一个新问题几乎没有研究。由于图是非线性数据结构,它是一个具有挑战性和有趣的研究领域,可以用来组织、模拟、建模和解决许多现实世界的问题,因此它在科学和商业领域都变得更加流行。图分析是许多应用程序的前提,包括考虑社交网络的应用程序,生物信息学、化合物、恐怖主义网络等等。FSM 构成了图聚类、基于图的异常检测和图分类的基础。
??FSM算法的主要任务是在大图
G
G
G 中搜索一组频繁子图
S
S
S,现有方法大多统计
G
G
G 中
S
S
S 的同构个数,如果这个数字大于或等于频率阈值
τ
\tau
τ(由用户给定),则
S
S
S 是频繁子图。几乎所有流行的 FSM 方法的计算成本都很高,并且需要两个阶段:
1、生成阶段:挖掘过程生成所有可用的候选子图,其中大小为
k
k
k 的频繁子图将生成大小为
(
k
+
1
)
(k + 1)
(k+1) 的候选子图;
2、测试阶段:检查并统计每个候选子图的同构数,以确定该候选子图是否频繁。
??然而,子图同构处理是一个众所周知的 NP 完全问题,因此该阶段的计算成本非常高。有一些关于 FSM 问题的新调查文章,这些论文通常侧重于分析和比较当前算法的方法和性能。因此,我们并不试图找出或比较挖掘算法之间的差异,而是关注 FSM 当前的问题以及解决这些问题的先进算法。我们还在这篇综述中考虑了 FSM 的两个阶段、主要群体和 FSM 的实际应用,作为未来参考和研究的基础。此外,我们提供了大量示例来说明挖掘过程中的步骤,并参考了许多最近解决 FSM 问题的论文。
概念和定义
??举一个现实生活中的例子,一家销售公司收集其客户的数据,并希望找到经常出现的客户群体来微调其业务策略。图 1 中的图
G
G
G 演示并建模了所有客户的列表。每个客户由属于标记为 A、B、C 或 D 的组的节点表示,两个节点的每条边表示这两个客户的关系(标记为 x、y、z、t 或 w)。图 1 中的子图
S
S
S 是该公司频繁购买群体的一个样本。
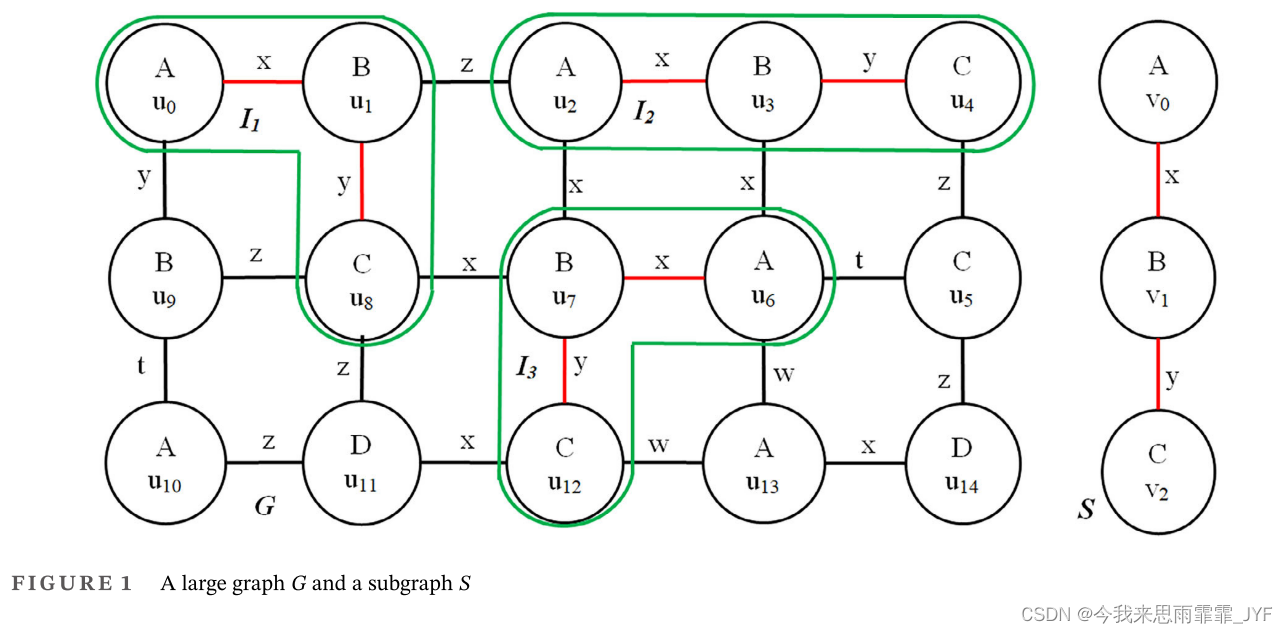
??找出所有频繁采购群体及其可能的实际采购次数,搜索结果有助于调整公司的经营策略。我们需要用一个大的图来模拟数据来解决这个问题,而客户组是子图。
定义1:图是一个三元组
G
=
(
V
,
E
,
L
)
G = (V, E, L)
G=(V,E,L),其中
V
V
V 是图
G
G
G 的所有节点的集合,
E
E
E 是图
G
G
G 的所有边的集合,
L
L
L 是为所有节点/边分配标签的函数。
定义2:图
S
=
(
V
S
,
E
S
,
L
S
)
S = ({V_S},{E_S},{L_S})
S=(VS?,ES?,LS?) 是大图
G
=
(
V
,
E
,
L
)
G = (V, E, L)
G=(V,E,L) 的子图,其中
V
S
?
V
{V_S} \subseteq V
VS??V,
E
S
?
E
{E_S} \subseteq E
ES??E,并且对于所有节点
v
∈
V
s
∪
E
s
v \in {V_s} \cup {E_s}
v∈Vs?∪Es? ,
L
s
(
v
)
=
L
(
v
)
{L_s}(v) = L(v)
Ls?(v)=L(v) 。
定义3:令
S
=
(
V
S
,
E
S
,
L
S
)
S = ({V_S},{E_S},{L_S})
S=(VS?,ES?,LS?) 为图
G
=
(
V
,
E
,
L
)
G = (V, E, L)
G=(V,E,L) 的子图。
S
S
S 到
G
G
G 的子图同构是单射函数
f
:
V
s
→
V
f:{V_s} \to V
f:Vs?→V。
示例 1: 在图 1 中,子图
S
S
S 具有表 1 中列出的三种不同的同构
I
1
,
I
2
,
I
3
{I_1},{I_2},{I_3}
I1?,I2?,I3?。

示例 2:在图 1 中,节点
v
0
{v_0}
v0?(子图
S
S
S)的域包括节点 {u0, u2, u6, u10, u13}(在大图
G
G
G 上)。
FSM 的两个阶段
??FSM 的目标是找到大图中出现次数大于或等于给定阈值
τ
\tau
τ 的所有子图。在图1中,我们知道
G
G
G 是单个大图,
S
S
S 是
G
G
G 中的样本子图。假设频率阈值
τ
=
2
\tau=2
τ=2,那么作为第一步的算法如GraMi、SuGraMi 和 WeGraMi 获取
G
G
G 中所有频繁边的列表,由 FE 列表表示,这些边具有满足阈值
τ
\tau
τ 的出现次数,因此:
E
F
=
{
A
x
?
B
,
B
y
?
C
,
C
z
?
D
}
EF = \{ A\mathop x\limits_ - B,B\mathop y\limits_ - C,C\mathop z\limits_ - D\}
EF={A?x?B,B?y?C,C?z?D}。
??通常,FSM 算法需要两个主要阶段:生成和测试,并使用方法在大图中搜索和统计候选者的同构。基于这两个阶段,算法侧重于减少冗余候选或方法,以降低测试阶段的成本。
生成阶段
??在此过程中,将通过添加新边来扩展频繁子图,以创建更大尺寸的候选子图。如Nguyen et al.(2020),在搜索树中,子图的支持总是小于或等于其父子图的支持。因此,在测试阶段只扩展频繁的子图生成候选子图,有助于在生成阶段减少大量不必要和冗余的候选子图。一些算法,如 SoGraMi 和 WeGraMi,使用向下闭包属性(DCP)对早期候选进行裁剪,减少了生成时间和处理那些不必要的候选所需的存储空间。
测试阶段
??所有生成的候选子图将被放入测试过程中,以确定它们是否频繁。当每个候选子图被确定为频繁时,流程将扩展这个子图以生成子候选子图,然后检查这些候选项是否频繁出现,然后生成过程递归地重复。如果候选子图不常见,流程将不会扩展它,因此测试阶段将不会实现。
??生成过程使用测试过程,因为将评估新的候选对象,以确定它们是否频繁出现。最近的算法搜索和计算子图同构的数目在一个大的图中。
在单个大型图上挖掘子图
??一般情况下,候选子图的出现频率是根据该子图在整个大图中出现的次数来确定的,大多数算法都使用该频率的DCP对搜索空间进行剪除。
??2014年,GraMi 算法提出了一种新的技术,可以快速有效地从单个大型图中挖掘频繁的子图,它只存储所有候选的模板,搜索同构,并在模板域中标记对应的值,而不是完全列出每个候选对象在大图上的所有表现(对应于它们的同构),因此该算法可以解决 FSM 问题。此外,GraMi 还进行了一些优化,以进一步提升其性能:(1)独特标签,下推剪枝、分解剪枝;(2)惰性搜索;(3)自同构。虽然GraMi克服了以往算法的缺点,但仍然存在一些主要的局限性:
非常长的执行时间:尽管GraMi可以克服以前许多增长-存储方法的局限性,但在该算法中求解同构仍然是一个 np 完全问题。该程序在两个阶段(生成和测试)都需要时间,其中生成的候选人数量非常多,每个待测试候选人的域也非常大,因此两个阶段所需的时间非常显著。
大内存需求:候选子图的数量巨大,系统需要存储和评估;对于大数据集,每个候选数据的存储域也很大,因此挖掘过程会消耗大量的存储空间。
FSM 的应用
??FSM经常被用来模拟或模拟各种领域中许多对象之间的复杂关系,如化学结构、计算机网络、社会网络、生物信息学、地图、计算机视觉和 web 分析。它在数据挖掘、知识表示和决策支持系统中发挥着重要作用。在本调查中,我们列出了一些FSM领域的优秀应用以及该应用的代表性算法。
??如今,企业或社交网络中的数据量越来越大,对于企业来说,从数据中收集、合成、表示和分析知识,以达到商业目的和分析人员(研究目的)的目的是非常重要的。表示知识的方法有很多,例如通过图表。图通常用于模拟或建模社交网络,其中顶点代表参与者,边描述参与者之间的关系。如今,社交网络越来越受到全球数十亿用户的欢迎。因此,社交媒体分析对于商业和研究目的变得必要。在线社交网络现在在互联网上发挥着重要作用。这些 SN 提出了一个具有挑战性的问题,并且包含大量数据。在SN中,FSM被广泛用于检测和识别网络中在线用户的频繁模式趋势,以分析和理解社会行为。其中,SN 中的频繁模式趋势被定义为数据集中特定频繁模式的时间戳出现(支持)值的序列。使用许多图来模拟和表示数据,然后使用图挖掘算法来分析和挖掘数据越来越普遍。2020 年,提出了一种新颖的 FSM 方法来发现和比较 SN 数据中存在的频繁模式趋势,称为排名频繁模式增长框架。此外,SN频繁模式趋势分析已经使用两个标准社交网络进行了评估,包括著名的MSNBC新闻网络和类Facebook网络数据集。
结论
??在本文中,我们回顾了最流行的 FSM 算法。近几十年来,这个问题得到了广泛的研究。我们概述了 FSM 的主题:(1)FSM 的两个主要阶段(生成阶段和测试阶段); (2) FSM的主要群体; (3) FSM的最新应用。在本文的主要部分中,我们提供了许多示例来详细说明 FSM 内部的步骤,并涵盖与所提到主题的每个部分直接相关的突出算法。本文对FSM的各个方面进行了总结,对相关算法和改进模型进行了分类,并列出了FSM的实际应用,作为今后研究和学习的基础。
??尽管FSM问题有很多算法和模型,但其复杂性仍然是NP-hard,并且对大图的处理仍然是一项成本极高的任务。与此同时,需要 FSM 的现实生活应用数量正在迅速增加,例如与社交网络、计算机网络、生物信息学、网络挖掘、化学结构、地图分析、计算机视觉和决策支持系统相关的应用。因此,FSM一直是一个有趣的问题,并且总是吸引着许多研究者。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!