7.8子集(LC78-M)

算法:
其实也是组合问题,还是用回溯。
与以前不同的是,如果把 子集问题、组合问题、分割问题都抽象为一棵树的话,那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!
其实子集也是一种组合问题,因为它的集合是无序的,子集{1,2} 和 子集{2,1}是一样的。
那么既然是无序,取过的元素不会重复取,写回溯算法的时候,for就要从startIndex开始,而不是从0开始!
什么时候for可以从0开始呢?
求排列问题的时候,就要从0开始,因为集合是有序的,{1, 2} 和{2, 1}是两个集合。
画树:
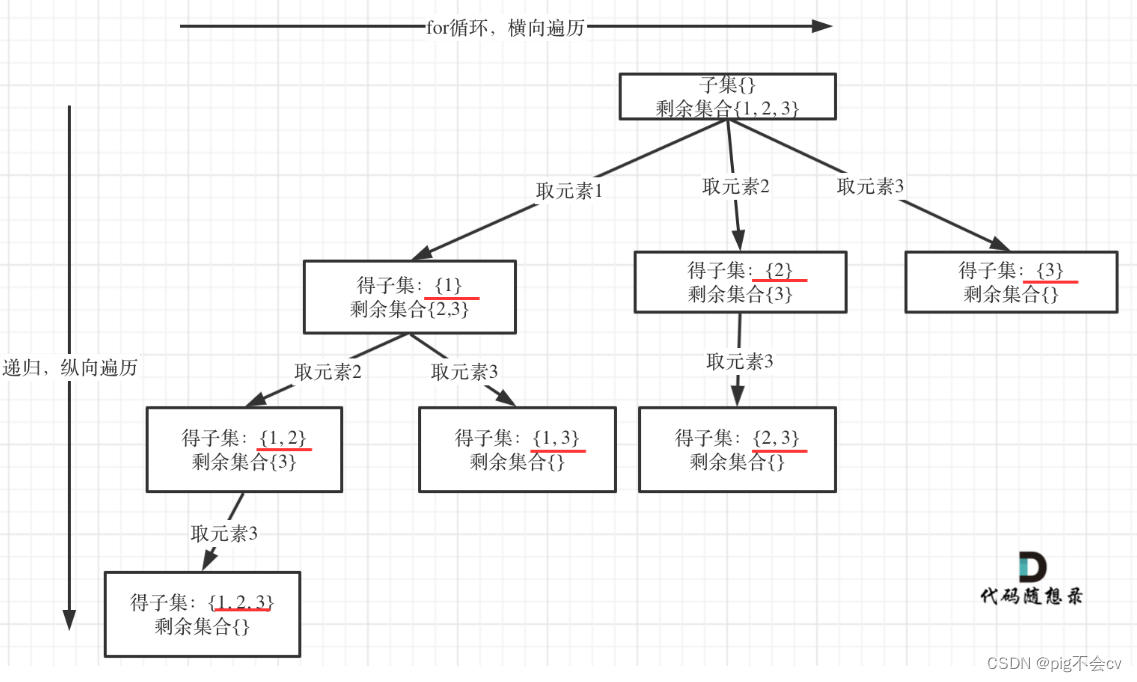
回溯三部曲:
1.确定返回值和参数
返回值:void
参数:int[] nums, int startindex
2.确定终止条件
剩余集合为空的时候,就是叶子节点。
什么时候剩余集合为空呢?
就是startindex已经大于数组的长度了,就终止了,因为没有元素可取了。
startindex >= nums.size()
3.单层递归逻辑
?求取子集问题,不需要任何剪枝!因为子集就是要遍历整棵树。
add 收集元素
递归
回溯,把刚刚收集的元素remove
调试过程:
class Solution {
//输出为二维数组,需要两个全局变量
List<List<Integer>> result = new LinkedList<>();
List<Integer> path = new LinkedList<>();
public List<List<Integer>> subsets(int[] nums) {
backtracking(nums,0);
return result;
}
void backtracking (int[] nums, int startindex) {
//每次递归时收集path
result.add(new LinkedList(path));
//确定终止条件,直接返回;
//这里不收集结果了,结果在单层递归时一个一个收集
if (startindex >= nums.size()) {
return;
}
//单层递归
for (int i = startindex; i < nums.size(); i++) {
path.add(nums[i]);
backtracking (nums, i+1);
path.removeLast();
}
}
}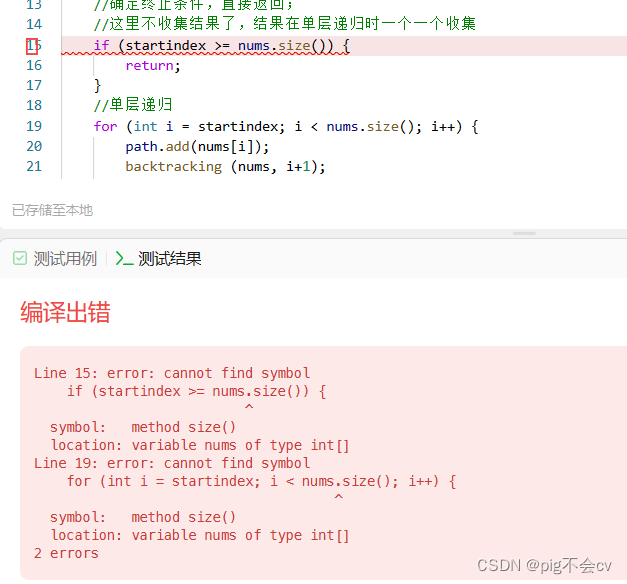
原因:
`nums.size()`?不是在 Java 中获取数组长度的有效语法。应该使用?`nums.length`。
java中,当处理字符串时,使用?`length()`?方法来获取其长度;而当处理数组时,使用?`length`?属性来获取其长度。
在 Java 中,针对字符串类型使用?`length()`?方法获取字符串的长度:因为字符串在 Java 中是作为对象处理的,因此使用方法(也就是要加个括号,length())来访问其属性或执行操作。字符串是 Java 中的内置类,因此它具有自己的方法和属性。
数组则是一种不同的数据结构。在 Java 中,数组是一种特殊的对象,但其长度是通过一个名为?`length`?的属性来获取,而不是一个方法。
正确代码:
class Solution {
//输出为二维数组,需要两个全局变量
List<List<Integer>> result = new LinkedList<>();
List<Integer> path = new LinkedList<>();
public List<List<Integer>> subsets(int[] nums) {
backtracking(nums,0);
return result;
}
void backtracking (int[] nums, int startindex) {
//每次递归时收集path
result.add(new LinkedList(path));
//确定终止条件,直接返回;
//这里不收集结果了,结果在单层递归时一个一个收集
if (startindex >= nums.length) {
return;
}
//单层递归
for (int i = startindex; i < nums.length; i++) {
path.add(nums[i]);
backtracking (nums, i+1);
path.removeLast();
}
}
}注意:
1.子集问题不用优化剪枝
2.子集问题的result收集位置位于递归函数的第一句话
3.子集问题、组合问题、分割问题,都是无序的,取过的元素不会重复取,写回溯算法的时候,for就要从startIndex开始,而不是从0开始!
时间空间复杂度:
时间复杂度: 
空间复杂度:
- O(n)。临时数组path的空间代价是?O(n),递归时栈空间的代价为?O(n)。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!