Linear Regression 线性回归

回顾

深度学习：

1. 数据集
2. 模型选择
3. 训练（KNN不需要）
4. 推理（预测）

线性回归

假设学生用x小时学习深度学习，能够得要y分数：

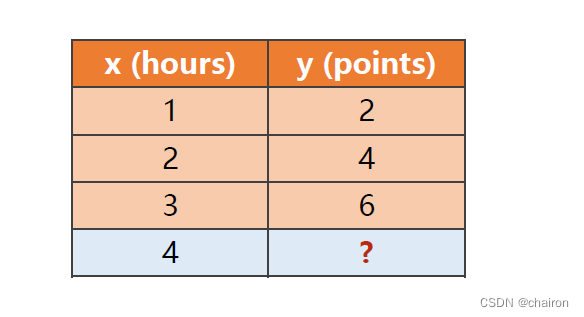
那么学习4小时，能够得到多少分？

用已知数据作为训练集：

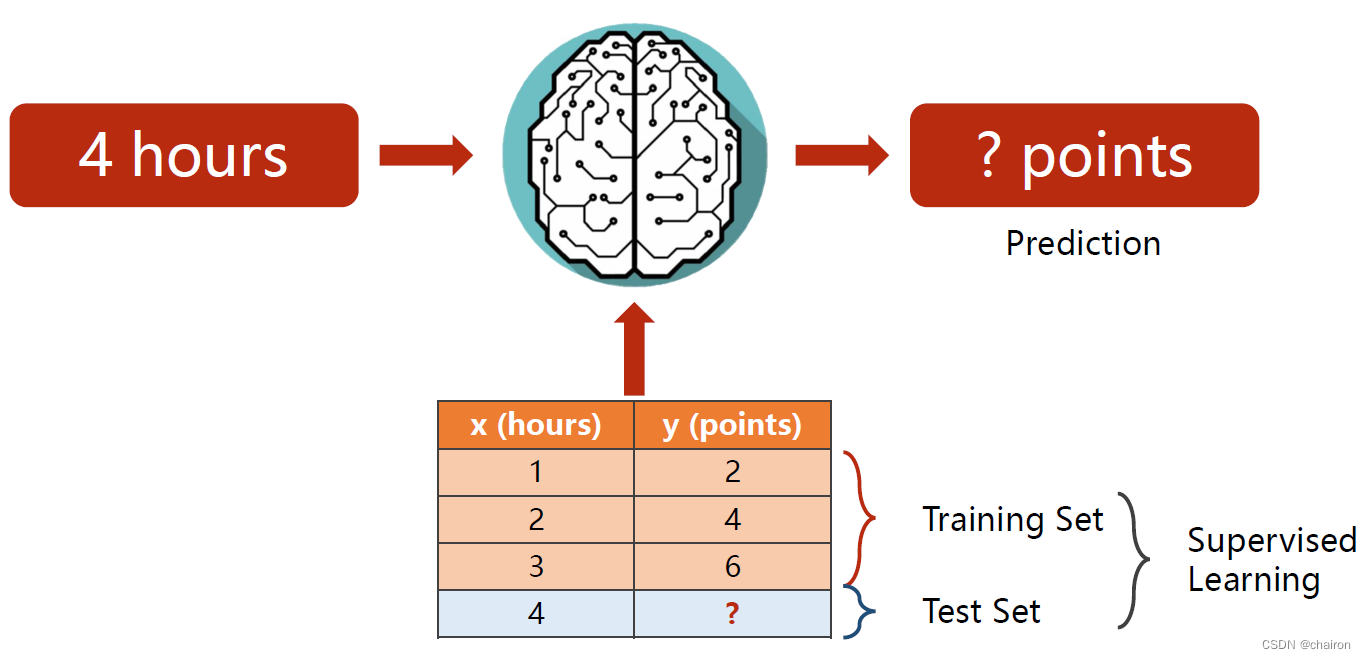
选取线性模型作为模型进行预测，线性模型是最简单的模型：𝑦=𝑥?𝜔+𝑏，我们需要求：𝜔、𝑏

在本次案例中，为了简化模型，使𝑦=𝑥?𝜔:

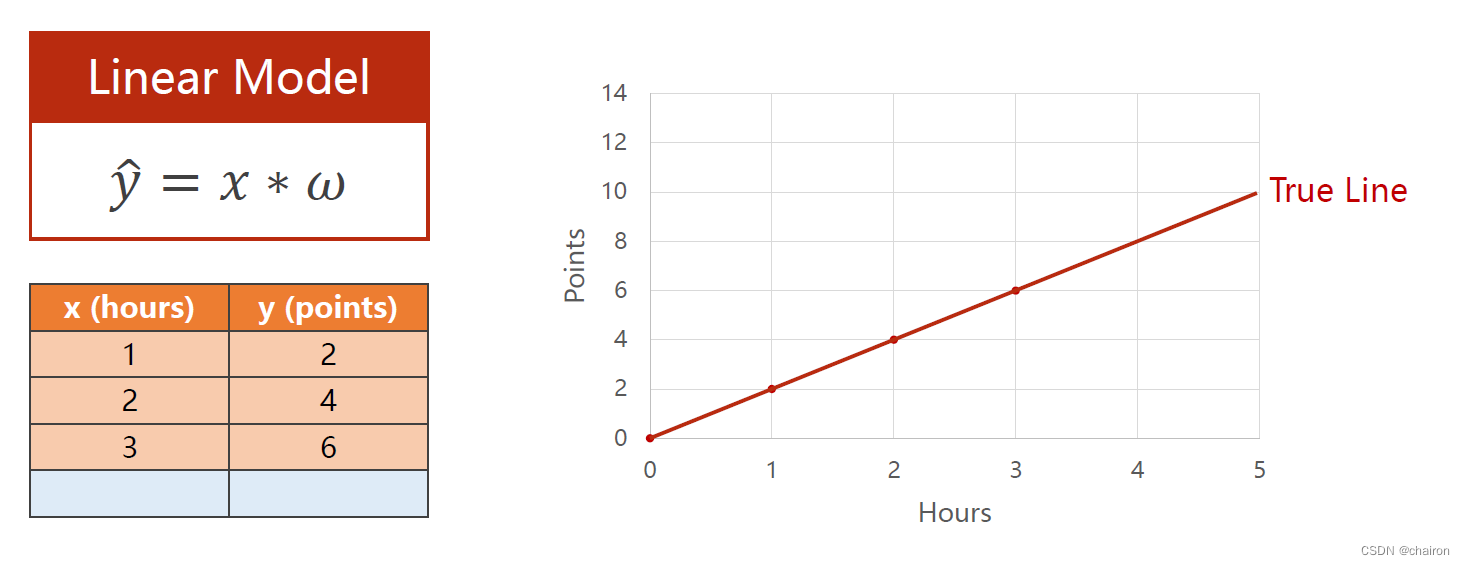
最开始𝜔是选取一个随机值，然后通过训练想要找到一个𝜔的取值使得生成的预测函数与真实值的差异尽可能小，即损失尽可能小。

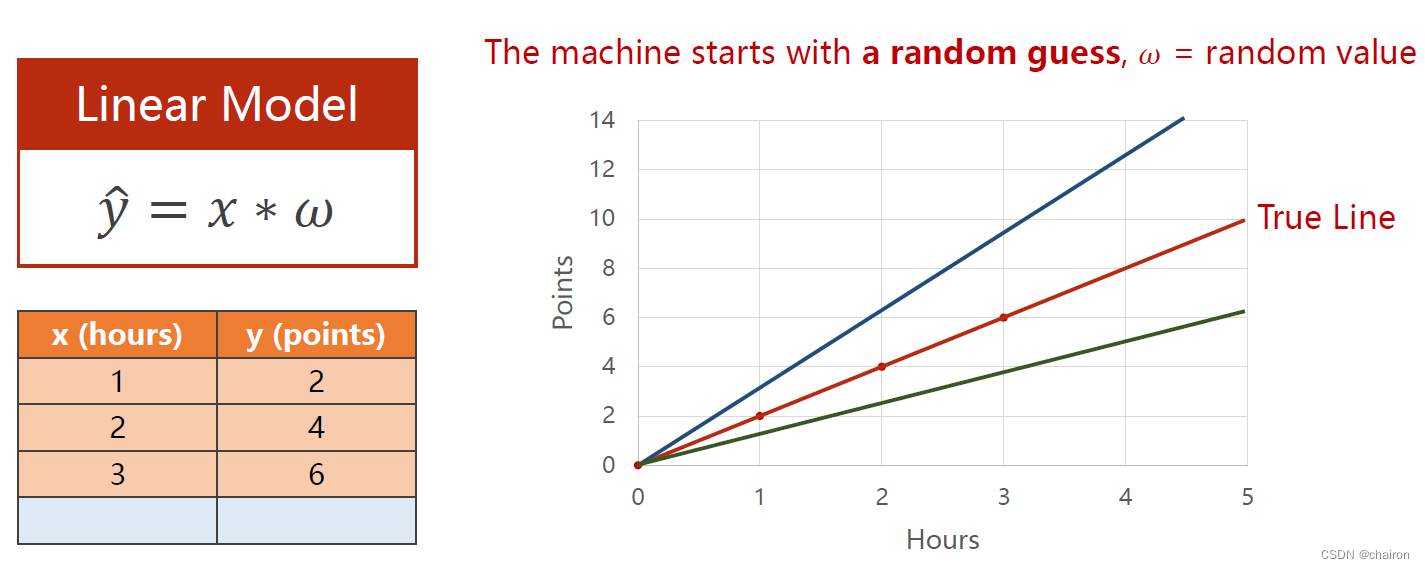
我们采用损失函数来衡量真实值与预测值之间的差异，目标就是：找到一个𝜔使得损失函数的值最小。
采用真实值与预测值的平方作为损失函数（loss)：
假设𝜔=3、4、0…，计算出每个样本的损失，之后求平均损失。目标就是找到一个𝜔使得这个平均损失最小：

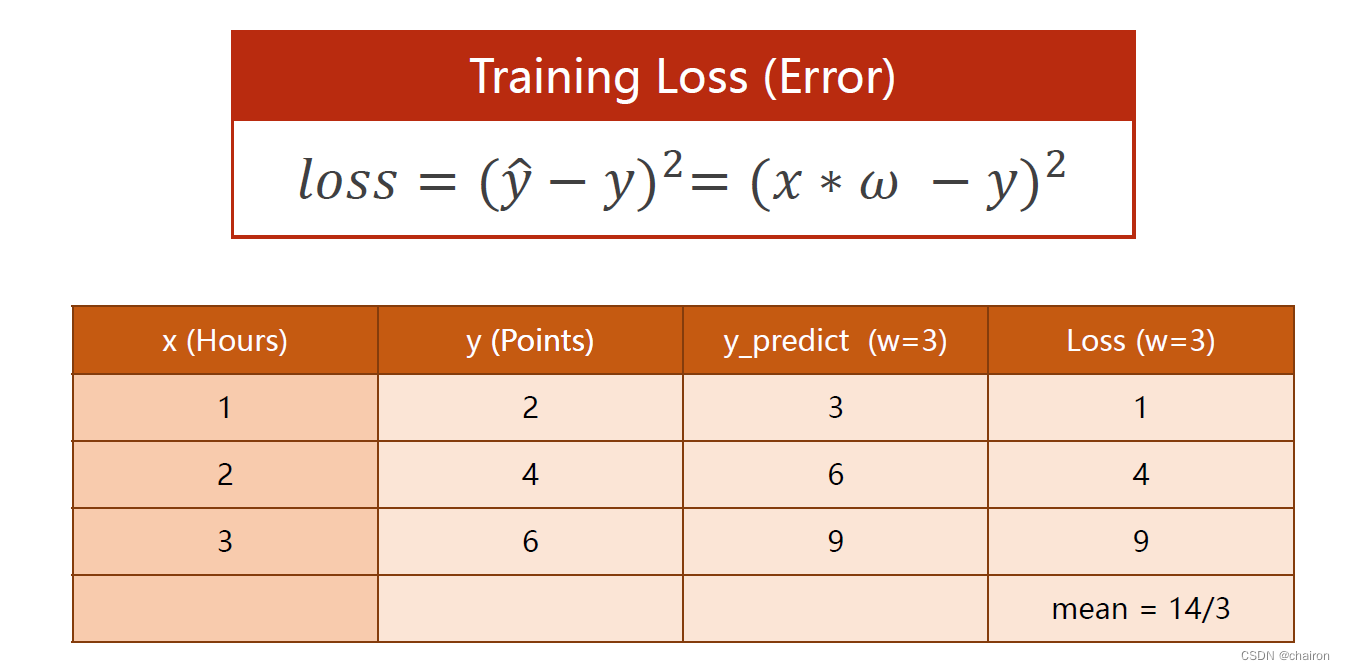
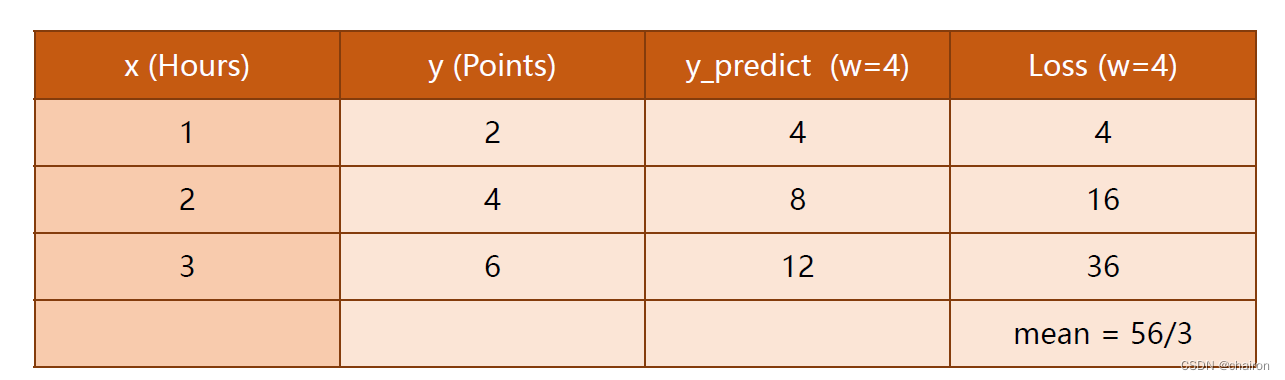
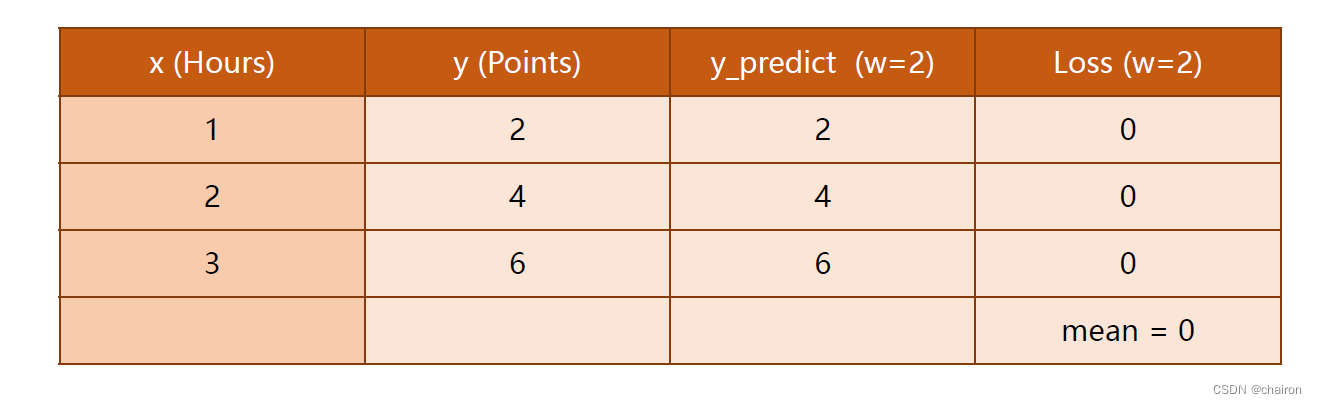
当𝜔=0时,平均误差为0，这是理想状态下最好的取值。是训练的理想目标！

注意：训练损失loss：是针对具体某一个样本的；将整个训练集的损失函数求平均（MSE）是最常用的损失函数cost之一：

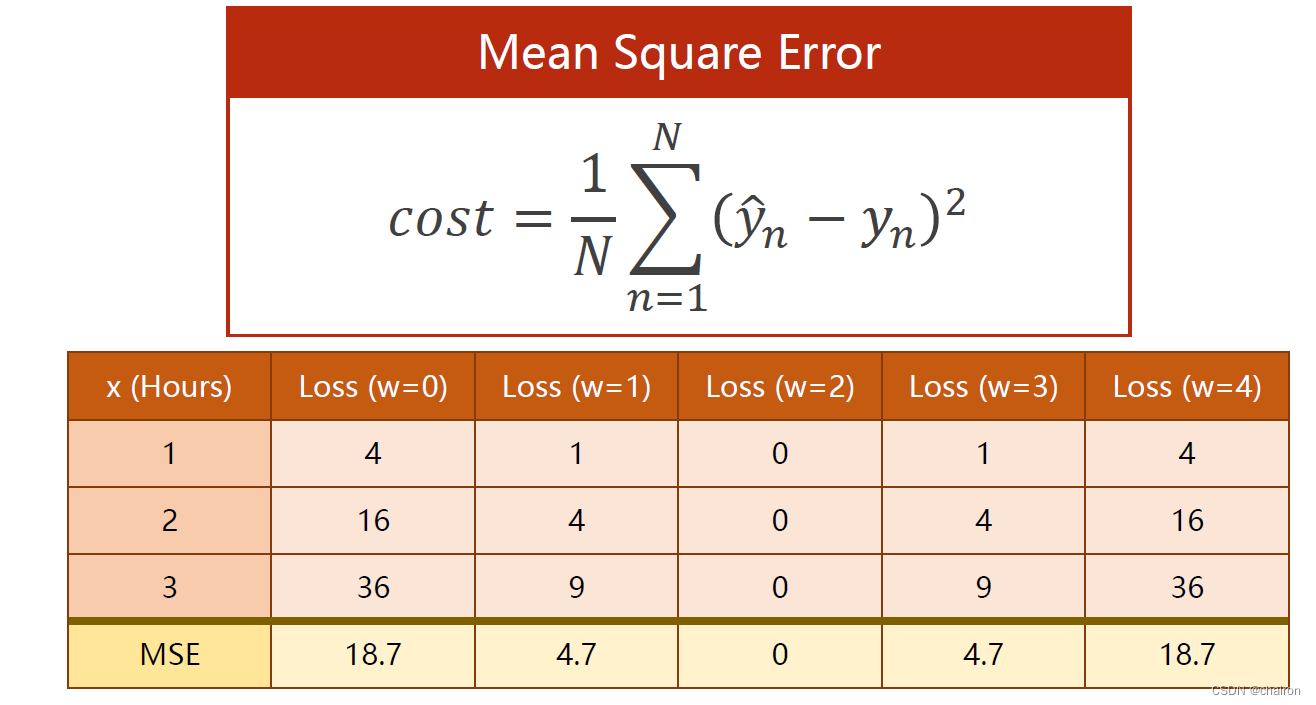
怎样才能找到最小的损失值呢？
假设损失值和w的关系如下图所示，我们可以采用穷举法将所有w取值的损失值都计算出来，就可以得到损失值的最小值是在w=3时取得的。

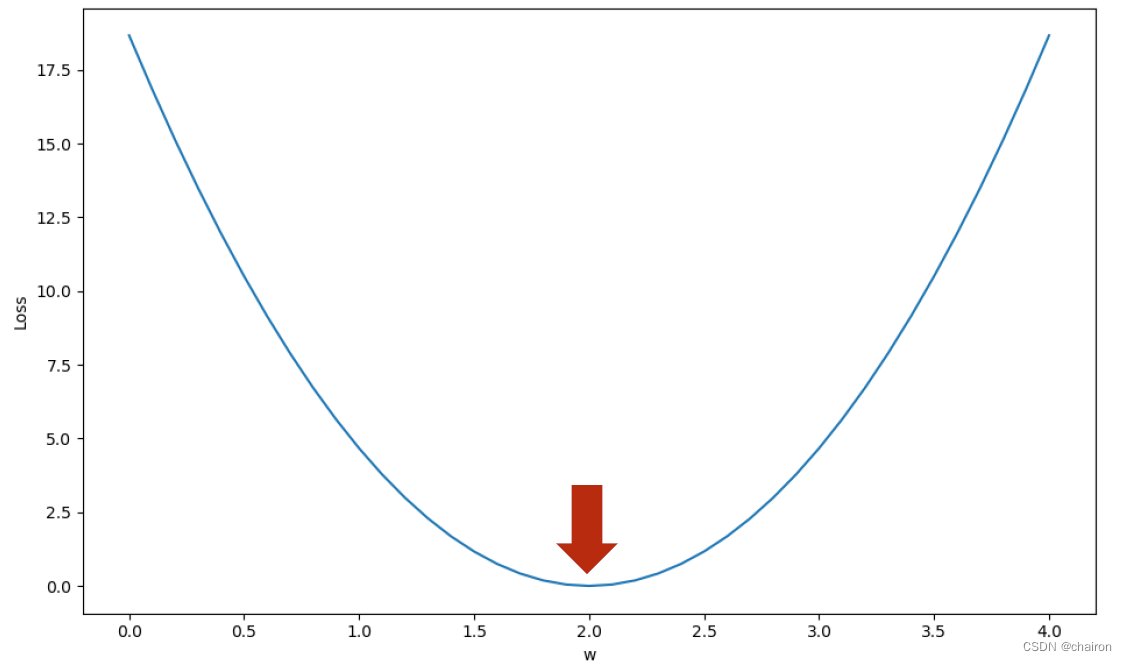
plt.plot()

plt.plot() 是Matplotlib库中用于==绘制线图（折线图）==的主要函数之一。
它的作用是将一组数据点连接起来，以可视化数据的趋势、关系或模式。以下是 plt.plot() 的详细介绍：
如果没有安装matplotlib库需要安装：pip install matplotlib

plt.plot(x, y, fmt, **kwargs)

x：表示X轴上的数据点，通常是一个列表、数组或一维序列，用于指定数据点的水平位置。
y：表示Y轴上的数据点，通常也是一个列表、数组或一维序列，用于指定数据点的垂直位置。
fmt：是一个可选的格式字符串，用于指定线条的样式、标记和颜色。例如，‘ro-’ 表示红色圆点线条。
**kwargs：是一系列可选参数，用于进一步自定义线条的属性，如线宽、标记大小、标签等。

以下是一些常用参数和用法：

样式参数（fmt）： 格式字符串可以包含一个字符来指定颜色，一个字符来指定标记样式，以及一个字符来指定线条样式。例如，‘r-’ 表示红色实线，‘bo–’ 表示蓝色圆点虚线。

线条样式（linestyle）： 使用linestyle参数可以指定线条的样式，如实线（‘-’）、虚线（‘–’）、点划线（‘-.’）等。

标记样式（marker）： 使用marker参数可以指定数据点的标记样式，如圆点（‘o’）、方块（‘s’）、星号（‘*’）等。

线条颜色（color）： 使用color参数可以指定线条的颜色，可以使用颜色名称（如’red’）、缩写（如’r’）或十六进制颜色码（如’#FF5733’）。

线宽（linewidth）： 使用linewidth参数可以指定线条的宽度，以数字表示。

标记大小（markersize）： 使用markersize参数可以指定标记的大小，以数字表示。

图例标签（label）： 使用label参数可以为线条指定标签，用于创建图例。

其他属性： 还有许多其他属性可用于自定义线图，如透明度、渐变、线型、阴影等。

plt.plot() 不仅可以绘制简单的线图，还可以用于绘制多条线，添加图例、标签、标题，设置坐标轴范围和刻度等。它是Matplotlib中最常用的绘图函数之一，适用于可视化数据集的趋势和关系。

import matplotlib.pyplot as plt
#显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
# 示例数据

x = [1, 2, 3, 4, 5]
y = [10, 15, 13, 18, 16]

# 绘制线图，并自定义外观
plt.plot(
    x,                         # X轴数据
    y,                         # Y轴数据
    marker='o',                # 标记样式：圆点
    linestyle='-',             # 线条样式：实线
    color='green',              # 线条颜色：蓝色
    linewidth=2,               # 线宽：2
    markersize=10,              # 标记大小：8
    label='数据1'               # 图例标签
)

# 添加标签和标题
plt.xlabel('X轴标签')
plt.ylabel('Y轴标签')
plt.title('标题')

# 添加图例
plt.legend()

# 显示网格线
plt.grid(True)

# 自定义刻度
plt.xticks([1, 2, 3, 4, 5], ['一', '二', '三', '四', '五'])

# 显示图表
plt.show()

参考博客

代码

import numpy as np
import matplotlib.pyplot as plt
#plt是常用的绘制图像的库
#训练集数据
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

#定义线性模型y=wx
def forward(x):
    return x * w

#定义损失函数:𝑙𝑜𝑠𝑠=(y_predect?𝑦)2=(𝑥?𝜔?𝑦)2
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2

# #定义w_list、mse_list来保存w和对应mes loss的取值
w_list = []
mse_list = []

#穷举法计算损失值cost
for w in np.arange(0.0, 4.1, 0.1):
    print("w=", w)
    l_sum = 0
    for x_val, y_val in zip(x_data, y_data):#x,y拼接为[x,y]
        y_pred_val = forward(x_val)#预测
        loss_val = loss(x_val, y_val)#求损失Loss
        l_sum += loss_val#Loss求和
        print('\t', x_val, y_val, y_pred_val, loss_val)
    print('MSE=', l_sum / 3)#计算mse
    w_list.append(w)
    mse_list.append(l_sum / 3)
    
#画图
plt.plot(w_list, mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

作业

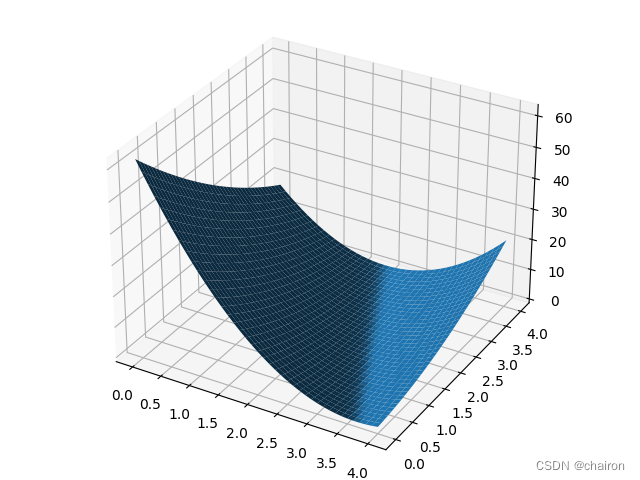
作业题目：实现线性模型（y=wx+b）并输出loss的3D图像。
提示：

1. 这里设函数为y=3x+1.5
   x_data = [1.0,2.0,3.0]
   y_data = [4.5,7.5,10.5]]
2. np.meshgrid()函数：X, Y = np.meshgrid(x, y) 代表的是将x中每一个数据和y中每一个数据组合生成很多点,然后将这些点的x坐标放入到X中,y坐标放入Y中,并且相应位置是对应的。详细解释

生成的loss图：