二分图及染色法判定
引例
在设计和开发电子政务和电子商务系统中,可能会碰到这样一类问题:单位有一些不同类型的工作空缺,也有一群申请填补这些空缺的应征者,每个人能胜任这些工作中的某些工作,于是就有如何聘任应征者,使得被聘任的人得到他适合的工作岗位的问题。这就是图论中的匹配问题。
假如我们用节点来表示应征者和岗位,应征者和其可胜任岗位之间用边相连,则有如下表示(p为应征者,m为岗位):
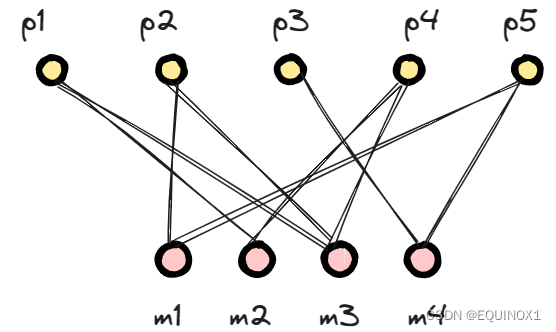
我们发现应征者之间没有边相连,同样的,岗位之间也没有边相连,这样一张图就引出了我们我们今天要介绍的主角——二分图。
二分图的定义
无向图的结点被分为两部分,这两部分各自内部的结点之间不相邻,结点相邻关系只出现在两部分之间的结点上,这种无向图称为二分图(Bipartite),也称二部图。
用数学语言描述就是:设G = (P , L)是图,P = P1 ∪ P2 , P1 ∩ P2 = ?,若P1、P2诱导子图均为零图,则称G为二分图(Bipartite)。
定理
图G是二分图,当且仅当G中所有回路长度均为偶数。
其实很好理解,因为每一条边都是从一个集合走到另一个集合,只有走偶数次才可能回到同一个集合。
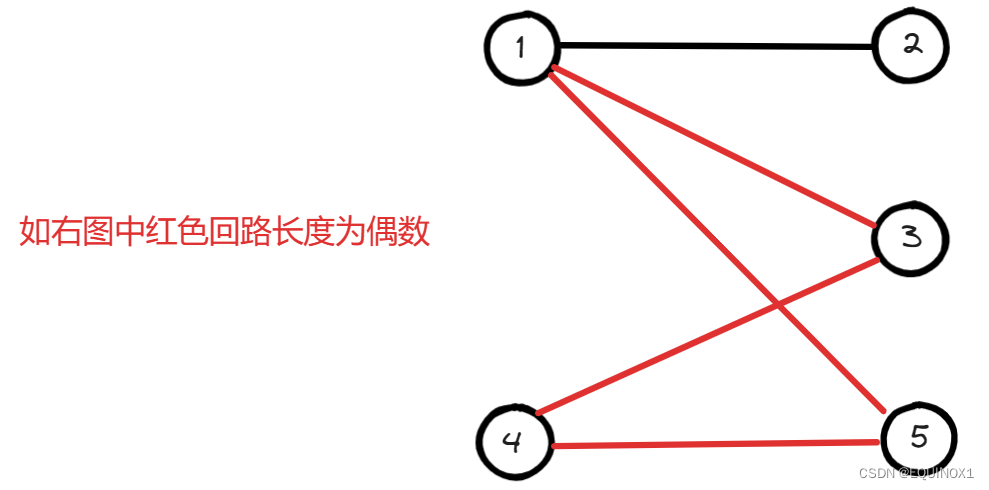
*证明(可略过)
我们就不给出严谨证明了,只粗略说明一下:
**必要性:**对于二分图G = P1 ∪ P2 ,如果有v0到v0的回路,不妨设v0在P1中,那么由于P1和P2各自内部节点无边相连,那么回路v0-v0必可表示为:v0,v1,v2,v3,v4…vk-1v0,其中vi ∈P2,当仅当i为奇数,则显然回路长度为偶数。
**充分性:**充分性,设图G中的所有回路的长度都为偶数,不妨设G为连通图,则任意两点间有路。
任取u∈P,令P = { v l v∈P且v到u的最短,路长度为偶数} , P2 = P - P1
则有P = P1 ∪ P2,P1 ∩ P2 = 0,下面证明P1和P2的诱导子图G1和G2都是零图
反证:假设G1不是零图,则存在w∈P1,v∈P,使得wv间有边,于是由u到w的最短路,边w和v到u的最短路构成一个长度为奇数的闭合路,若该闭合路不是回路,则除去在计算路长中被计算过两次的边之外,可分为若干个回路的并,且其中至少有一个回路的长度为奇数.与G中的所有回路的长度都为偶数矛盾.于是G1是零图。同理证明G2也是零图
故G是二分图.
推论
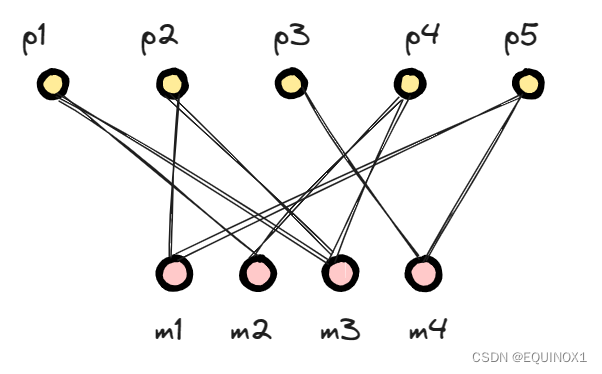
二分图是2-可着色的。
比如我们最开始这个例子,应聘者和岗位分为了两种颜色。
二分图判定——染色法
我们可以使用染色法来判定二分图。即尝试用两种颜色标记图中的节点,当一个点被标记后,所有与它相邻的节点应该标记与它相反的颜色,若标记过程产生冲突,则说明图中存在奇环。可以用DFS或BFS来实现。
染色法实现
数据结构
我们首先需要存图结构,我们这里使用链式前向星,实际中根据数据情况选择合适存图结构。
关于链式前向星,见:链式前向星详解
#define N 1000005
int head[N], idx = 0;
struct edge
{
int v, nxt;
} edges[N];
当然,既然是染色法当然要存储颜色,我们用数组colour存储颜色,为染色情况默认为0
int colour[N]{0};
算法流程
- 颜色数组colour初始化为0,被访问的点的颜色是1或2。
- dfs(u,c)进入u,将u点染色为c。
- 枚举u的邻点v,
(1)若v未访问,深搜v并对v染色,若返回有奇环,则一路返回有奇环。
(2)若v已访问且v的颜色与u的颜色相同,则返回有奇环。 - 枚举完u的邻点,没有发现奇环,则返回没有奇环。
代码详解:
bool dfs(int x, int c)
{
colour[x] = c;
for (int i = head[x]; ~i; i = edges[i].nxt)
{
int v = edges[i].v;
if (!colour[v])
{
if (dfs(v, 3 - c))
return true;
}
else if (colour[v] == c)
return true;
}
return false;
}
OJ练习
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!