2023/12/17 n层正方形

【问题描述】编写程序，输出n层正方形图案。正方形图案最外层是第一层，每层用的数字和层数相同。

【输入形式】正方形图案的层数n

【输出形式】2n-1行2n-1列数据，一行上的数据用一个空格分隔

【样例输入】

3

【样例输出】

1 1 1 1 1

1 2 2 2 1

1 2 3 2 1

1 2 2 2 1

1 1 1 1 1

【样例说明】3层图案，最外层都是1，里面一层都是2，最里面一层只有一个数3，所以是5×5的矩形。

这个题历来有很多做法。我的老师，我的学长，我自己感觉有三种做法。（也许？）?

老师的做法如下，他的代码注释很详细，我就不再过多解释了

#include <iostream>
// #include <math.h>
#include <cmath>
#define MAX_NUM (100)
using namespace std;
int main(void)
{
    // 输入层数n
    size_t n = 1;
    cin >> n;

    // 正方形的大小 n+n-1
    size_t NUM = n + n - 1;

    // 建议给学生这样讲，二维动态数组不见得兼容
    int arr[MAX_NUM][MAX_NUM];      

    // 规律 从1开始，每进一层step 数字+1
    for (size_t step = 0; step < n; step++)
    {
        // 每进一层，边框横坐标 -1
        for (size_t i = step; i < NUM-step; i++)
        {
             每进一层，边框纵坐标 -1
            for (size_t j = step; j < NUM-step; j++)
            {
                // 找到缩小后矩阵的边框 上框、左框
                if ((i == step) || (j == step) )                
                {
                    arr[i][j] = step + 1;
                }

                // 找到缩小后矩阵的边框 下框、右框
                if((i == (NUM-step-1)) || (j == (NUM - step-1))){
                    arr[i][j] = step + 1;
                }
            }
        }
    }

    // 输出矩阵
    for (size_t i = 0; i < NUM; i++)
    {
        for (size_t j = 0; j < NUM; j++)
        {

            cout << arr[i][j]<< ' ';
        }
        cout << endl;
    }
}

第二种是学长的做法。他是从这个图形的对称性入手解决问题。这里贴出他的文章链接：

观察结构，发现所要输出的方阵根据主对角线(左上到右下)对称，因此只需找到输出主对角线以上(含主对角线)的部分即可。

首先解决主对角线(第一组数)，主对角线数字顺序为1，2，……，n－1，n , ?n－1，……，2，1也是对称的，且根据 n 对称。为了方便起见，令for语句中 i 的初始值为1，则此时每个 i 对应的都是arr[i－1][i－1]。为了方便描述，不妨将数组中的元素命名为m，当 i ＜＝n时，m＝i；当i > n时，m＝2* n－i。

此时主对角线 ?(第一行第一列，第二行第二列，……，第2* n－1行第2* n－1列) ? 解决完毕，下面来看第二组 ?(第一行第二列，第二行第三节，……，第2* n－2行第2* n－1列) ?。

此时第二组数的总数为2* n－2，此时最中间的数为n－1(此时最中间的数有两个，但无妨)，此时每个 i 对应的数组元素是arr[i－1][i－1＋]〕(即arr[i－1][ i ])，同样用m代替。和第一组类似，当 i＜＝n时，m＝i；当 i > n时，由于第二组总数个数为偶数，因此第一组公式不合适，因此需要找一个同时适用于奇数个数和偶数个数的公式。此时考虑第三组数(第一行第三列，第二行第四列，……，第n－3行第n－1列) 最中间的数字也是n－1，进一步证明了上面那个公式不合适。接下来有两种方法解决这个问题 :

方法一 ??
只讨论奇数组(1、3、5、……、2* n－1组)?

这时第一组数中那个公式就可以用了，即第 j 组数的个数为2* n－j，最中间的数为(2* n－j＋1)/2 ?(不妨记为n1)，当 i＜＝n1时，m＝i；当i ? >n1时，m＝2*n1－i 将所有奇数组放到一个for循环中

这时可以发现，所有空缺的偶数组的数都是前面的数和后面的数的平均数

方法二 ??
从出现的问题出发，找到一个新的公式

为了方便起见，不妨拿n＝3举例，此时第一组数为1，2，3，2，1；第二组数为1，2，2，1；如果按照上面那个公式第一组数在 i >3时，依次为2*3－4，2*3－5 ?第二组数在 i >2时，依次为2*2－3，2*2－4 显然第二组数与我们想要得到的不同，结果差了1，因此考虑如何才能得到我们想要的结果，也许(2*2＋1)-3，(2*2＋1)-4可以得到，这里可以用if条件语录，但是有些繁琐，我们需要得到一个适用于所有情况的公式，第 j 组中间的数为n－j(记作a)，第 j 组数的个数为2* n－1-j(记作b)，由2* a－1＝b可得，a＝( b＋1)/2 ?(此时不论b为奇数还是偶数，由int整型得到的a为一个整数)，于是 i > n1时公式可以改为m＝2* a－i，此时将所有数放到for循环中。

以上两个方法自行选择

得到主对角线及主对角线以上部分的数后，主对角线下的数就很容易得到了，由矩阵对称可令a[i-1-j][i-1]＝a[i－1][i-1-j] ? ?于是，所要求得的矩阵就完全求出了

运算部分需要有嵌套循环，内层为 i 的循环，i 表示第几行，外层为m的循环，i + m表示第几列
————————————————
版权声明：本文为CSDN博主「玄殛~」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/m0_73552988/article/details/127855127

http://t.csdnimg.cn/TqZS1http://t.csdnimg.cn/TqZS1第三种是我自己的想法。我拿到这个问题先观察了它给出的样例，发现了一个小窍门（应该算是？）

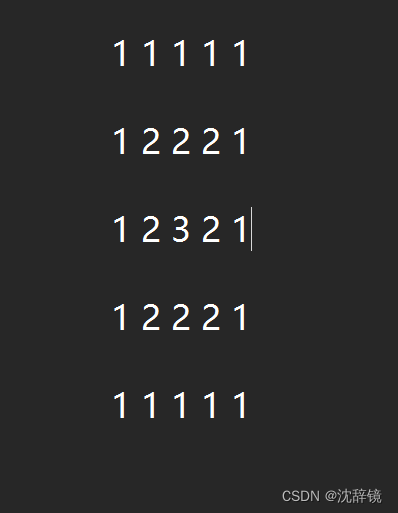
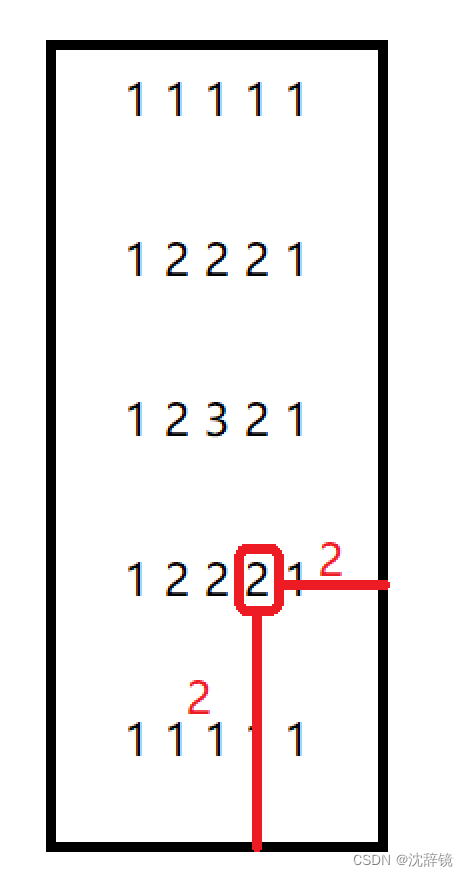
我们来观察这个图案。每个位置所对应的数字其实是该位置到四条边的距离取最小值。如果说1到四条边的距离为1，那么我们可以如下图推出每一个位置所对应的数字。比如下图。

这样就可以通过代码解决问题了。?

#include<iostream>
using namespace std;

int main()
{
	int n;
	cin >> n;
	for (int i = 0; i < 2 * n - 1; i++)
	{
		for (int j = 0; j < 2 * n - 1; j++)
		{
			int num = min(min(i, j), min(2 * n - i - 2, 2 * n - j - 2))+1;
			cout << num << " ";
		}
		cout << endl;
	}

	return 0;
}