QTNet:Query-based Temporal Fusion with Explicit Motion for 3D Object Detection
参考代码:QTNet
动机和出发点
自动驾驶中时序信息对感知性能具有较大影响,如在感知稳定性维度上。对于常见的时序融合多是在feature的维度上做,这个维度的融合主要分为如下两个方案:
- 1)BEV-based方案:将之前帧的结果按照ego-motion进行warp之后再叠加融合,这样的操作简单,但低效且引入较多无关噪声
- 2)Proposal-based方案:将目标做RPN,然后再将多帧RPN之后的特征融合起来,这样的操作是高效,但是对proposal有质量要求
这俩方案具有各自的优缺点,那么基于query的方式便是一种折中的考量了,query中包含了物体语义信息,reference point中包含了位置信息,而这篇文章提出的方案便是在query的维度上对齐(按照距离作为度量对齐),之后再去做感知预测。那么上面三种时序方案各自的实现过程和对比见下图所示:
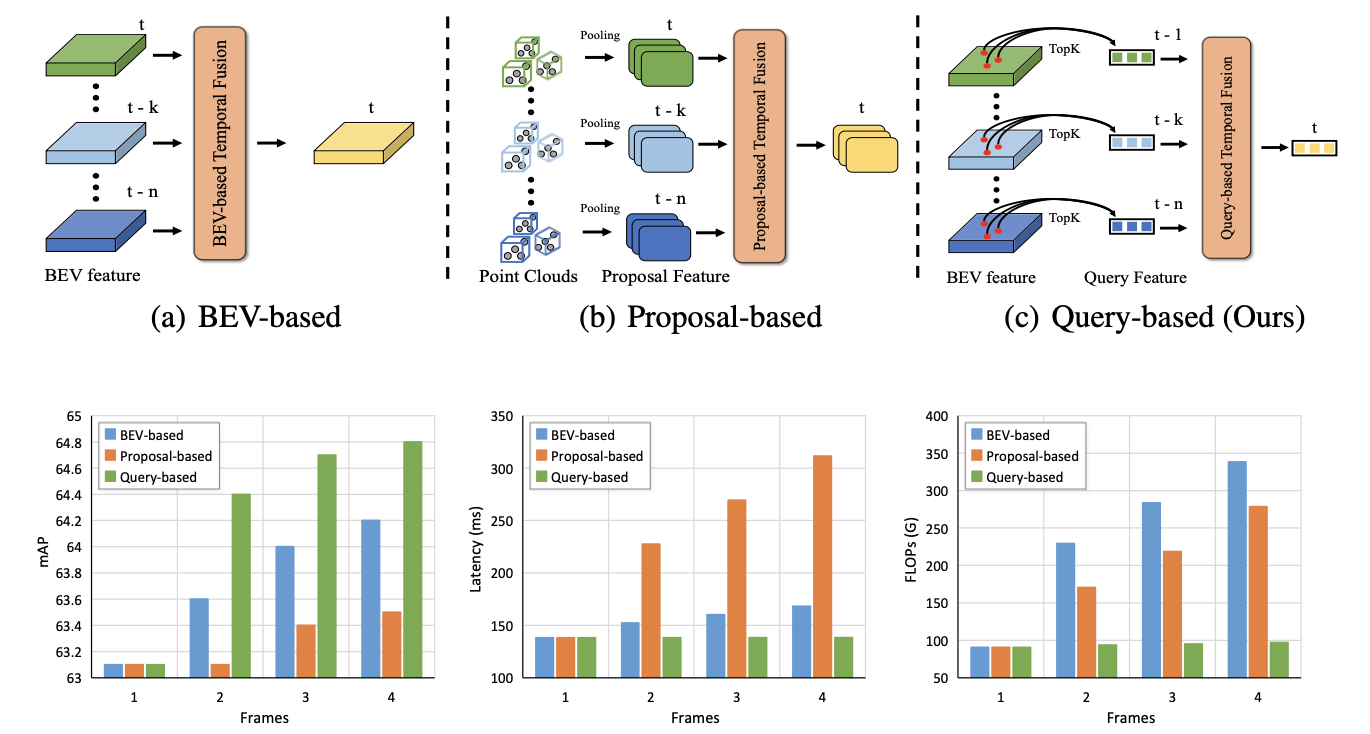
其实在了解完整篇文章的思路之后会觉得文章的方案其实并不是那么靠谱,在文章的方案中分类、速度预测、ego-motion精度等是关键因素,直接影响了attn-mask的质量,要是这些拉垮了,那就完犊子了。并且这个机制更加适合障碍物的检测,那么对于其它的感知任务就不是那么友好了,扩展性比较差。反倒个人更加倾向cross-attn的方式(如StreamPETR)。
方法的设计
要使用到时序信息,那么自然的就需要添加一个FIFO队列去存储之前帧的信息,再使用一个时序融合网络去融合多帧的信息,对此下图中的M模块(参数是共享的)便是完成这个工作的,并且是按照时间帧级连的过程。下图是结构图:
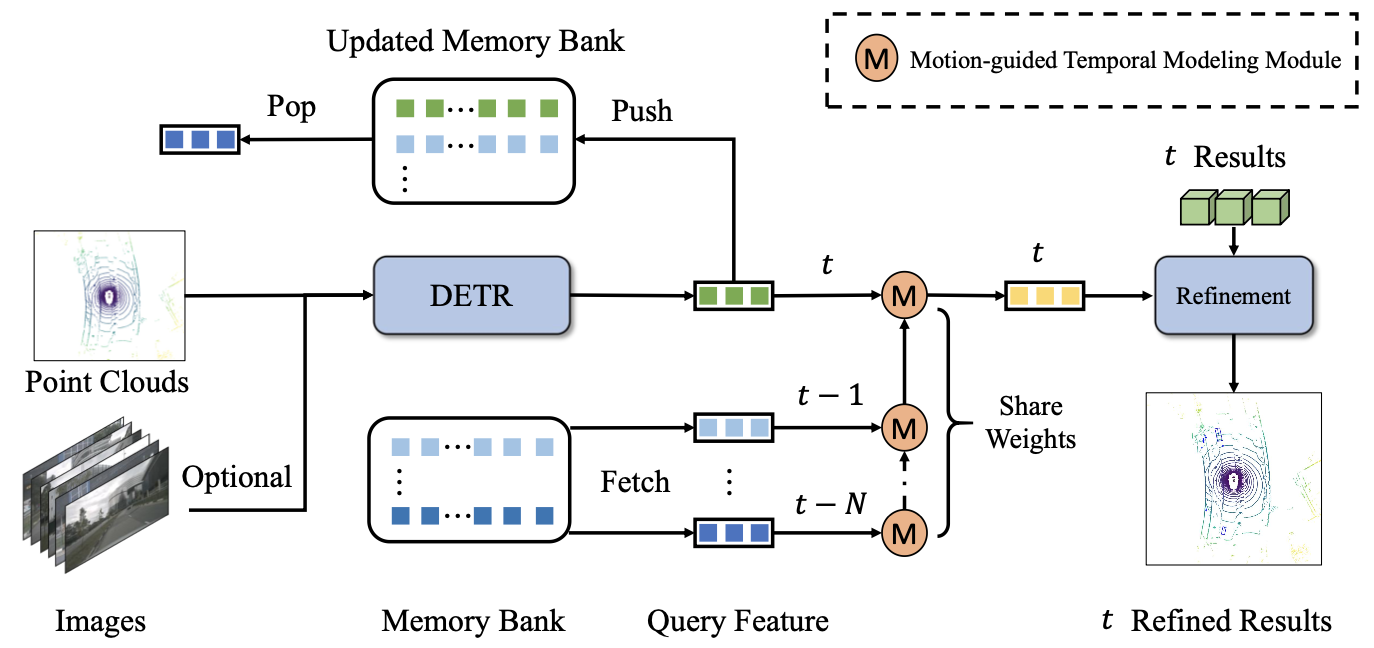
时序融合过程
假设之前帧的query和reference point分别表示为
Q
t
?
1
′
,
C
t
?
1
Q^{'}_{t-1},C_{t-1}
Qt?1′?,Ct?1?,那么在ego-motion下实现前一帧道当前帧的变换
R
t
?
1
t
R_{t-1}^t
Rt?1t?,则可推出reference point的对齐变换关系为:
C
t
?
1
′
=
(
C
t
?
1
+
V
t
?
1
Δ
t
)
?
(
R
t
?
1
t
)
T
C_{t-1}^{'}=(C_{t-1}+V_{t-1}\Delta t)\cdot (R_{t-1}^t)^T
Ct?1′?=(Ct?1?+Vt?1?Δt)?(Rt?1t?)T
那么依据reference point之间的距离度量:
O
t
?
1
t
=
L
2
(
C
t
?
C
t
?
1
′
)
O_{t-1}^t=L_2(C_t-C_{t-1}^{'})
Ot?1t?=L2?(Ct??Ct?1′?)
那么再结合分类的结果
s
t
s_t
st?和距离阈值
γ
\gamma
γ可以得到不同query之间的度量,从而得到attn-mask:
M
=
{
0
,
if?
O
t
?
1
t
≤
γ
?and?
s
t
=
s
t
?
1
1
e
8
,
if?
O
t
?
1
t
≥
γ
?or?
s
t
≠
s
t
?
1
M= \begin{cases} 0, & \text{if $O_{t-1}^t\le \gamma$ and $s_t=s_{t-1}$} \\ 1e8, & \text{if $O_{t-1}^t\ge \gamma$ or $s_t\neq s_{t-1}$} \end{cases}
M={0,1e8,?if?Ot?1t?≤γ?and?st?=st?1?if?Ot?1t?≥γ?or?st?=st?1??
则对应的attn-weight描述为(注意原文少个括号):
A
=
s
o
f
t
m
a
x
(
?
1
?
(
O
t
?
1
t
+
M
)
)
A=softmax(-1\cdot(O_{t-1}^t+M))
A=softmax(?1?(Ot?1t?+M))
这样经过加权之后的前一帧query再和当前帧做融合,这样级连优化query的表达,如下图所示:
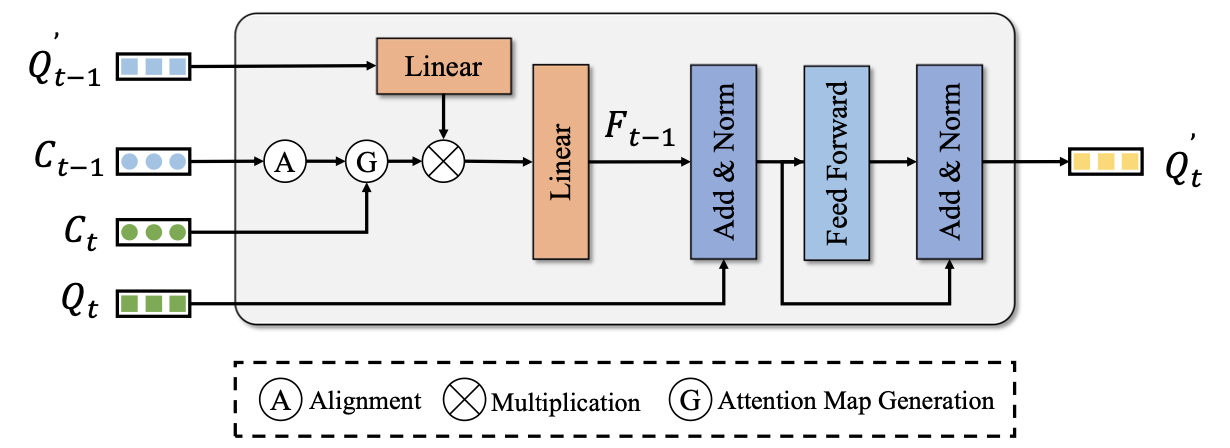
回归和分类是否需要解耦
对于级连优化query的方式在回归和分类上是share与否可以将时序融合划分为两种类型(一般来讲都是解耦好些):
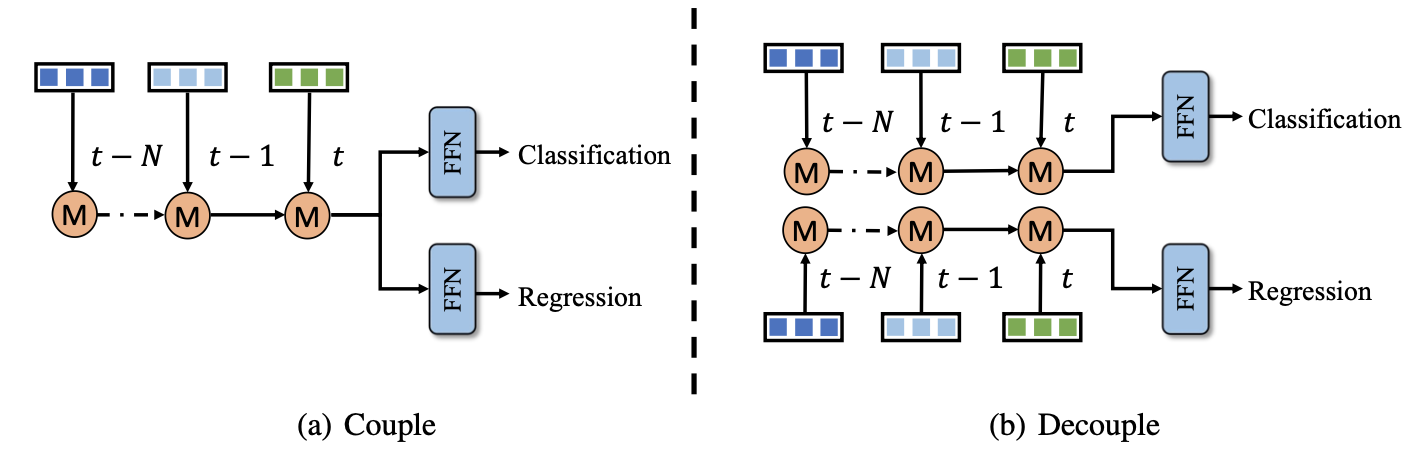
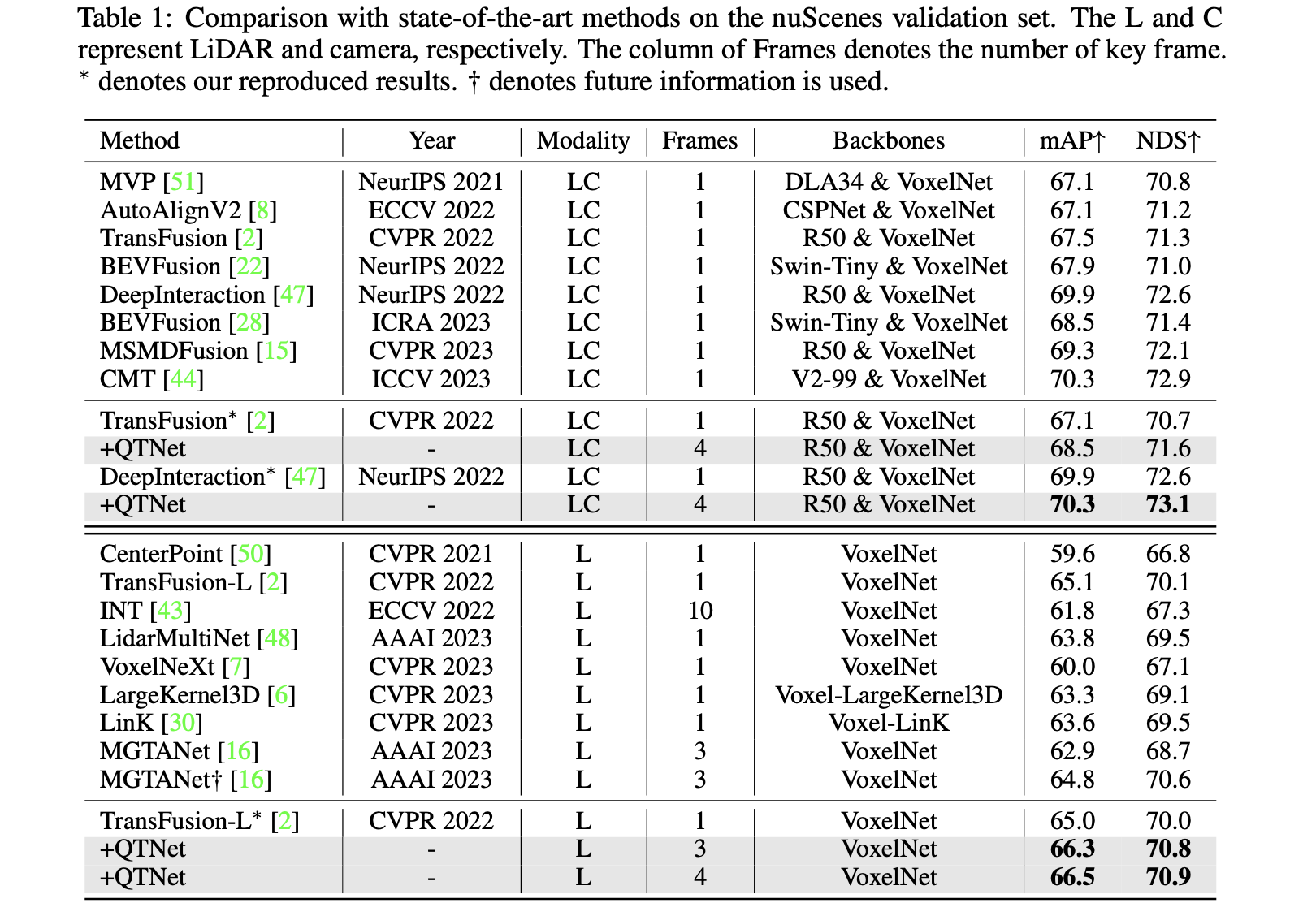
实验结果
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!