一文浅谈旋转变换：旋转矩阵、旋转向量、欧拉角、四元数

{
    //point
    const Eigen::Vector3d a(1.0, 2.0, 3.0);
    //Rotation Matrix
    Eigen::Matrix3d R;
    R << -0.243982607, -0.969731574, -0.009652007,
          0.969362354, -0.244157481,  0.026902609,
         -0.028444919, -0.002792523,  0.999591461;
    //Axis-Angle
    const double angle = 1.817567592; //rad
    const Eigen::Vector3d axis(-0.015311407, 0.009690003, 0.999835819); //is unit vector
    //Euler Angles
    const double alpha = -0.002792527, beta = 0.028448867, gamma = 1.817448093;
    //Quaternion
    const double qw = 0.614705493, qx = -0.012076975, qy = 0.007643055, qz = 0.788627217;
}

一、旋转矩阵

旋转矩阵乘以向量后改变向量的方向，但不改变长度。（unitary operation的保长和保角）

1.1 定义和推导

先说结论：

旋转矩阵由旋转前后两坐标系对应的两组基的内积得到。由于基是标准正交基，所以旋转矩阵是行列式为1、秩为阶数的正交矩阵，且各元素是各基向量夹角的余弦值（有限取值范围）。

已知向量在标准正交基中的坐标计算公式： $\lambda _{i}=\vec{e}_{i}^{T} \vec{a}=\begin{bmatrix} \vec{a},\vec{e}_{i} \end{bmatrix}$

现有三维向量空间V，取标准正交基 $\left ( \vec{e}_{1},\vec{e}_{2},\vec{e}_{3} \right )$ ，经过旋转，变成了 $\left ( \vec{e'}_{1},\vec{e'}_{2},\vec{e'}_{3} \right )$ 。由标准正交基的性质（两两正交、单位向量），以及正交矩阵的充要条件，可知旋转前后两组基构成的三阶方阵均是正交矩阵。

对于向量 $\vec{a}$ ，其在空间的位置并不会随着坐标系的旋转而发生运动，因此根据向量在标准正交基中的坐标计算公式，并取向量在两坐标系的坐标分别为 $\begin{bmatrix} a_{1} & a_{2} & a_{3} \end{bmatrix}^{T}$ 和 $\begin{bmatrix} a'_{1} & a'_{2} & a'_{3} \end{bmatrix}^{T}$ ，则有：

$\begin{bmatrix} \vec{e'}_{1} & \vec{e'}_{2} & \vec{e'}_{3} \end{bmatrix} \begin{bmatrix} a_{1}'\\ a_{2}'\\ a_{3}' \end{bmatrix} = \begin{bmatrix} \vec{e}_{1} & \vec{e}_{2} & \vec{e}_{3} \end{bmatrix} \begin{bmatrix} a_{1}\\ a_{2}\\ a_{3} \end{bmatrix} ........ \left ( 1-1 \right )$

对式(1-1)等号两边同时左乘正交矩阵 $\begin{bmatrix} \vec{e'}_{1} & \vec{e'}_{2} & \vec{e'}_{3} \end{bmatrix}^{T}$ ：

$\begin{bmatrix} \vec{e'}^{T}_{1}\\ \vec{e'}^{T}_{2}\\ \vec{e'}^{T}_{3} \end{bmatrix} \begin{bmatrix} \vec{e'}_{1} & \vec{e'}_{2} & \vec{e'}_{3} \end{bmatrix} \begin{bmatrix} a'_{1}\\ a'_{2}\\ a'_{3} \end{bmatrix} = \begin{bmatrix} \vec{e'}^{T}_{1}\\ \vec{e'}^{T}_{2}\\ \vec{e'}^{T}_{3} \end{bmatrix} \begin{bmatrix} \vec{e}_{1} & \vec{e}_{2} & \vec{e}_{3} \end{bmatrix} \begin{bmatrix} a_{1}\\ a_{2}\\ a_{3} \end{bmatrix} ........ \left ( 1-2 \right )$

式(1-2)等号左边两正交矩阵相乘（正交矩阵定义式）的结果是三阶单位阵，等号右边两正交矩阵的乘积是三阶正交阵（两正交矩阵相乘结果仍是正交矩阵），所以可得：

$\begin{bmatrix} a'_{1}\\ a'_{2}\\ a'_{3} \end{bmatrix} = \begin{bmatrix} \vec{e'}^{T}_{1} \vec{e}_{1} & \vec{e'}^{T}_{1} \vec{e}_{2} & \vec{e'}^{T}_{1} \vec{e}_{3} \\ \vec{e'}^{T}_{2} \vec{e}_{1} & \vec{e'}^{T}_{2} \vec{e}_{2} & \vec{e'}^{T}_{2} \vec{e}_{3} \\ \vec{e'}^{T}_{3} \vec{e}_{1} & \vec{e'}^{T}_{3} \vec{e}_{2} & \vec{e'}^{T}_{3} \vec{e}_{3} \end{bmatrix} \begin{bmatrix} a_{1}\\ a_{2}\\ a_{3} \end{bmatrix} ........ \left ( 1-3 \right )$

式(1-3)中的系数矩阵即是旋转矩阵R：

$R = \begin{bmatrix} \vec{e'}^{T}_{1} \vec{e}_{1} & \vec{e'}^{T}_{1} \vec{e}_{2} & \vec{e'}^{T}_{1} \vec{e}_{3} \\ \vec{e'}^{T}_{2} \vec{e}_{1} & \vec{e'}^{T}_{2} \vec{e}_{2} & \vec{e'}^{T}_{2} \vec{e}_{3} \\ \vec{e'}^{T}_{3} \vec{e}_{1} & \vec{e'}^{T}_{3} \vec{e}_{2} & \vec{e'}^{T}_{3} \vec{e}_{3} \end{bmatrix} ........ \left ( 1-4 \right )$

所以：

$\vec{a'}=R \vec{a} \ ........ \left ( 1-5 \right )$

由正交矩阵的性质，有：

$R^{-1} = R^{T} \\ = \begin{bmatrix} \vec{e'}^{T}_{1} \vec{e}_{1} & \vec{e'}^{T}_{1} \vec{e}_{2} & \vec{e'}^{T}_{1} \vec{e}_{3} \\ \vec{e'}^{T}_{2} \vec{e}_{1} & \vec{e'}^{T}_{2} \vec{e}_{2} & \vec{e'}^{T}_{2} \vec{e}_{3} \\ \vec{e'}^{T}_{3} \vec{e}_{1} & \vec{e'}^{T}_{3} \vec{e}_{2} & \vec{e'}^{T}_{3} \vec{e}_{3} \end{bmatrix}^{T} = \begin{bmatrix} \vec{e}^{T}_{1} \vec{e'}_{1} & \vec{e}^{T}_{1} \vec{e'}_{2} & \vec{e}^{T}_{1} \vec{e'}_{3} \\ \vec{e}^{T}_{2} \vec{e'}_{1} & \vec{e}^{T}_{2} \vec{e'}_{2} & \vec{e}^{T}_{2} \vec{e'}_{3} \\ \vec{e}^{T}_{3} \vec{e'}_{1} & \vec{e}^{T}_{3} \vec{e'}_{2} & \vec{e}^{T}_{3} \vec{e'}_{3} \end{bmatrix} ........ \left ( 1-6 \right )$

若对式(1-1)等号两边同时左乘正交矩阵 $\begin{bmatrix} \vec{e}_{1} & \vec{e}_{2} & \vec{e}_{3} \end{bmatrix}^{T}$ ：

$\begin{bmatrix} \vec{e}^{T}_{1}\\ \vec{e}^{T}_{2}\\ \vec{e}^{T}_{3} \end{bmatrix} \begin{bmatrix} \vec{e'}_{1} & \vec{e'}_{2} & \vec{e'}_{3} \end{bmatrix} \begin{bmatrix} a'_{1}\\ a'_{2}\\ a'_{3} \end{bmatrix} = \begin{bmatrix} \vec{e}^{T}_{1}\\ \vec{e}^{T}_{2}\\ \vec{e}^{T}_{3} \end{bmatrix} \begin{bmatrix} \vec{e}_{1} & \vec{e}_{2} & \vec{e}_{3} \end{bmatrix} \begin{bmatrix} a_{1}\\ a_{2}\\ a_{3} \end{bmatrix} ........ \left ( 1-7 \right )$

两边矩阵相乘后可得：

$\begin{bmatrix} \vec{e}^{T}_{1} \vec{e'}_{1} & \vec{e}^{T}_{1} \vec{e'}_{2} & \vec{e}^{T}_{1} \vec{e'}_{3} \\ \vec{e}^{T}_{2} \vec{e'}_{1} & \vec{e}^{T}_{2} \vec{e'}_{2} & \vec{e}^{T}_{2} \vec{e'}_{3} \\ \vec{e}^{T}_{3} \vec{e'}_{1} & \vec{e}^{T}_{3} \vec{e'}_{2} & \vec{e}^{T}_{3} \vec{e'}_{3} \end{bmatrix} \begin{bmatrix} a'_{1}\\ a'_{2}\\ a'_{3} \end{bmatrix} = \begin{bmatrix} a_{1}\\ a_{2}\\ a_{3} \end{bmatrix} ........ \left ( 1-8 \right )$

将式(1-6)代入(1-8)有：

$\vec{a}=R^{-1} \vec{a'}=R^{T} \vec{a'} \ ........ \left ( 1-9 \right )$

直接定义旋转矩阵和使用的示例代码如下：

//code
{
    //point
    const Eigen::Vector3d a(1.0, 2.0, 3.0);

    Eigen::Matrix3d R;
    R << -0.243982607, -0.969731574, -0.009652007,
          0.969362354, -0.244157481,  0.026902609,
         -0.028444919, -0.002792523,  0.999591461;
    std::cout << std::setprecision(9) << std::fixed;
    std::cout << "Rotation Matrix: " << R.determinant() << std::endl << R << std::endl << std::endl;
    std::cout << "(1.0, 2.0, 3.0) after rotation (by matrix): " << std::endl << (R*a).transpose() << std::endl << std::endl;

    #if 1
    Eigen::Matrix4d T = Eigen::Matrix4d::Identity();
    T.block<3, 3>(0, 0) = R;
    T.block<3, 1>(0, 3) = Eigen::Vector3d(11, 22, 33);
    std::cout << "Transform Matrix: " << std::endl << T << std::endl << std::endl;
    #else
    Eigen::Isometry3d T = Eigen::Isometry3d::Identity();
    // T.rotate(R);
    T.prerotate(R);
    T.pretranslate(Eigen::Vector3d(11, 22, 33));
    std::cout << "Transform Matrix: " << std::endl << T.matrix() << std::endl << std::endl;
    #endif
}

//print
Rotation Matrix: 1.000000000
-0.243982607 -0.969731574 -0.009652007
 0.969362354 -0.244157481  0.026902609
-0.028444919 -0.002792523  0.999591461

(1.0, 2.0, 3.0) after rotation (by matrix): 
-2.212401776  0.561755219  2.964744418

Transform Matrix: 
-0.243982607 -0.969731574 -0.009652007 11.000000000
 0.969362354 -0.244157481  0.026902609 22.000000000
-0.028444919 -0.002792523  0.999591461 33.000000000
 0.000000000  0.000000000  0.000000000  1.000000000

1.2?旋转矩阵的缺点

①表达方式冗余不紧凑。旋转只有三个自由度，但本节的旋转矩阵均有九个量。

②旋转矩阵必须是正交矩阵，且行列式为1。这些约束使估计或优化一个旋转矩阵变得困难。

③不方便直观理解。

二、旋转向量

前述旋转矩阵的表达方式存在冗余不紧凑，而任意的旋转，实际都可用一个旋转轴和一个旋转角来刻画。

2.1 定义和推导

定义一个向量，其方向与旋转轴一致，长度等于旋转角，将该向量称之为旋转向量（或轴角/角轴，Axis-Angle）。而使用三维向量就可以表示三自由度的旋转。

为了便于表示，旋转轴取为单位向量 $\vec{n}$ ，旋转角为θ，那么旋转向量 $\left ( \theta \vec{n} \right )$ 就可以表示绕此旋转轴的任一旋转。

//code
{
    const double angle = 1.817567592; //rad
    const Eigen::Vector3d axis(-0.015311407, 0.009690003, 0.999835819); //is unit vector
    const Eigen::AngleAxisd V(angle, axis);
    std::cout << "Axis-Angle: " << axis.norm() << std::endl << "angle=" << V.angle() << ", axis=" << V.axis().transpose() << std::endl << std::endl;
    std::cout << "(1.0, 2.0, 3.0) after rotation (by angle): " << std::endl << (V*a).transpose() << std::endl << std::endl;
    // std::cout << "(1.0, 2.0, 3.0) after rotation (by angle):" << std::endl << (Eigen::AngleAxisd(std::atan(1.0/2.0), Eigen::Vector3d::UnitZ())*a).transpose() << std::endl << std::endl; //rotate around the Z-axis
}

//print
Axis-Angle: 1.000000000
angle=1.817567592, axis=-0.015311407  0.009690003  0.999835819

(1.0, 2.0, 3.0) after rotation (by angle): 
-2.212401777  0.561755216  2.964744418

2.1.1 旋转向量转旋转矩阵

直接使用罗德里格斯公式：

$R=cos\theta \cdot I+\left ( 1-cos\theta \right )\cdot \vec{n} \vec{n}^{T}+sin\theta \cdot \vec{n}^{\wedge} \ ...... \left ( 2-1 \right )$

tips: 式(2-1)中符号^表示向量对应的唯一的反对称矩阵，形如：

$\vec{n}^{\wedge}=\begin{bmatrix} 0 & -n_{3} & n_{2}\\ n_{3} & 0 & -n_{1}\\ -n_{2} & n_{1} & 0 \end{bmatrix}$

? ? ? ? 反对称矩阵具有以下特性：

$\left ( \vec{n}^{\wedge} \right )^{T}=-\left ( \vec{n}^{\wedge} \right ) \\ \vec{n}^{\wedge} \vec{n}=\vec{0} \ //column \ vector \\ \vec{n}^{T}\vec{n}^{\wedge} =\vec{0}^{T} \ //row \ vector$

? ? ? ? 此外，反对称矩阵可将两个定义在同一个坐标系的向量的叉积运算转换为矩阵和向量的乘法运算，即：

$\left ( \vec{a} \times \vec{b}\right )\rightarrow (\vec{a}^{\wedge} \vec{b})=-\left ( \vec{b}^{\wedge} \vec{a} \right )$

//code
{
    const auto V2R = V.toRotationMatrix(); //V.matrix() == V.toRotationMatrix()
    std::cout << "Axis-Angle to Rotation Matrix: " << V2R.determinant() << std::endl << V2R << std::endl << std::endl;
}

//print
Axis-Angle to Rotation Matrix: 1.000000001
-0.243982607 -0.969731574 -0.009652007
 0.969362354 -0.244157481  0.026902608
-0.028444918 -0.002792524  0.999591461

2.1.2?旋转矩阵转旋转向量

即是要把旋转轴对应的单位向量 $\vec{n}$ 和旋转角θ逆推出来：

（1）计算旋转角θ

可以对式(2-1)两边同时求迹：

$tr(R)=cos\theta \cdot tr(I)+\left ( 1-cos\theta \right )\cdot tr(\vec{n} \vec{n}^{T})+sin\theta \cdot tr(\vec{n}^{\wedge}) \ ...... \left ( 2-2 \right )$

tips: ①迹即方阵特征值之和，方阵的主对角线元素之和。

????????②单位列向量与其转置的乘积，是一个秩为1的，迹为1的，实对称的，任意两行（列）成比例的，且任意次方都等于本身的方阵。

所以式(2-2)可化简为：

$tr(R)=3cos\theta +\left ( 1-cos\theta \right )=1+2cos\theta \ ...... \left ( 2-3 \right )$

由此可得旋转角θ为：

$\theta=arccos\frac{tr(R)-1}{2} \ ........ \left ( 2-4 \right )$

（2）计算单位向量 $\vec{n}$ 表征的旋转轴

对于旋转轴上的向量，旋转发生后是不会发生变化的。因此对于表征旋转轴的单位向量 $\vec{n}$ ，有以下恒等式：

$R \vec{n}=\vec{n} \ ........ \left ( 2-5 \right )$

上式表明旋转轴 $\vec{n}$ 是三阶方阵R对应于特征值1的特征向量，解此特征向量，再归一化，即得所需旋转轴。式(2-5)可进一步转换成齐次线性方程组形式，如下：

$(R-I) \vec{n}=\vec{0} \ ........ \left ( 2-6 \right )$

齐次线性方程组有非零解的充要条件是系数矩阵的秩小于阶数，但 $(R-I)$ 矩阵并不一定满足，所以可能只有零解，因此应避免使用该转换方式。

//code
{
    #if 0
    // const Eigen::AngleAxisd R2V(R);
    Eigen::AngleAxisd R2V;
    // R2V = R; //overloaded operator
    R2V.fromRotationMatrix(R);
    std::cout << "Rotation Matrix to Axis-Angle: " << R2V.axis().norm() << std::endl << "angle=" << R2V.angle() << ", axis=" << R2V.axis().transpose() << std::endl << std::endl;
    #else
    const double R2V_angle = std::acos(0.5*(R.trace()-1));
    const Eigen::EigenSolver<Eigen::MatrixXd> es(R);
    // std::cout << "eigenvalues: " << std::endl << es.eigenvalues().real().transpose() << std::endl;
    // std::cout << "eigenvectors: " << std::endl << es.eigenvectors().real() << std::endl;
    const auto eigenvalues = es.eigenvalues().real();
    int idx = 0;
    for (const auto val : eigenvalues) {
        if (1.0e-6 > std::fabs(val - 1.0)) {
            break;
        }
        idx++;
    }
    if (eigenvalues.rows() > idx) {
        const auto R2V_axis = es.eigenvectors().real().block<3, 1>(0, idx);
        std::cout << "Rotation Matrix to Axis-Angle: " << R2V_axis.norm() << std::endl << "angle=" << R2V_angle << ", axis=" << R2V_axis.transpose() << std::endl << std::endl;
    }
    #endif
}

//print
Rotation Matrix to Axis-Angle: 1.000000000
angle=1.817567592, axis=-0.015311407  0.009690003  0.999835819

2.2 旋转向量的缺陷

①存在奇异性（当 $\theta =0^{\circ} \ or \ \theta =180^{\circ}$ 时？？？）。

②不方便直观理解。

三、欧拉角

针对旋转矩阵和旋转向量不能直观描述旋转，欧拉角则通过将一个旋转分解成三次绕不同轴的旋转，使旋转过程变得可以理解。

tips: 若未特殊说明，旋转方向默认按右手螺旋方向，即从旋转轴正半轴向坐标原点看，逆时针方向为正，顺时针方向为负。

3.1 定义和推导

使用欧拉角描述旋转，需知道以下三个信息才能明确刚体的姿态：

①绕三轴旋转的角度(α,β,γ)，分别对应(x,y,z)三个坐标轴。也可用yaw-pitch-roll（偏航-俯仰-横滚）表示，但其与坐标轴的对应关系受限于各领域的定义。

②旋转顺序。一般有两类排序系列，一类是X-Z-X系列（经典欧拉角），一类是X-Z-Y系列（泰特布莱恩角）：
????????Proper Euler angles: X-Z-X, X-Y-X, Y-X-Y, Y-Z-Y, Z-Y-Z, Z-X-Z
????????Tait–Bryan angles: X-Z-Y, X-Y-Z, Y-X-Z, Y-Z-X, Z-Y-X, Z-X-Y（SLAM中常使用）

③内旋还是外旋。内旋使用旋转之后的轴，外旋使用固定轴。（内外旋等效性：内旋效果等价于颠倒顺序后的外旋效果，证明省略）
? ? ? ? 假设使用Z-Y-X旋转顺序，即先绕Z轴旋转γ，旋转过后，原坐标系的X、Y轴变成X'、Y'，Z轴不变，得到新的坐标系X'Y'Z。第二次旋转β角时，内旋是按照第一次旋转后X'Y'Z坐标系的Y'轴旋转，而外旋仍是按原坐标系中的Y轴旋转。第三次旋转类似。下图描述内旋过程：

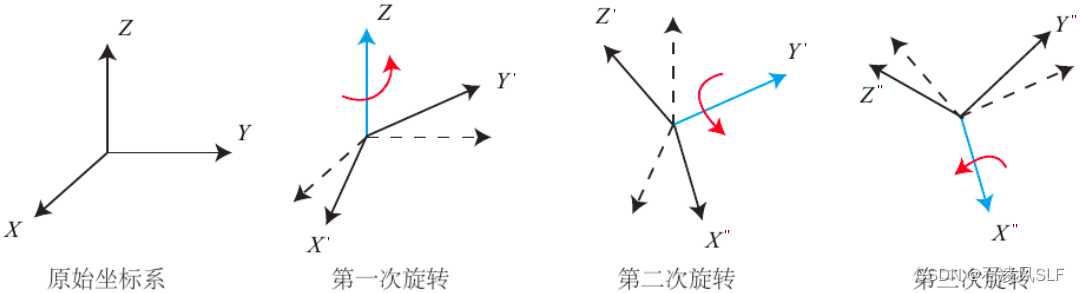
在[wiki]描述旋转顺序时，表示内旋的第二、第三旋转轴的字母右上角分别会标记一撇和两撇（以与上一次旋转后的轴对应），如下图所示。本文在描述旋转顺序时不遵循此方式，内外旋以文字显式说明。如Z-X-Y仅指示旋转轴的顺序，第二第三轴是使用旋转前还是旋转后，具体会辅以文字说明。

使用欧拉角描述旋转主要是为了方便主观理解，其并不能像前述旋转矩阵和旋转向量那样，直接左乘就能表示旋转。最终一般还是要转换为旋转矩阵，或者四元数来参与计算。

//code
{
    const double alpha = -0.002792527, beta = 0.028448867, gamma = 1.817448093;
    Eigen::Vector3d E(alpha, beta, gamma); //rad
    std::cout << "Euler Angles: (x,y,z)→(α,β,γ), intrinsic sequence z-x-y" << std::endl << E.transpose() << std::endl << std::endl;
}

//print
Euler Angles: (x,y,z)→(α,β,γ), intrinsic sequence z-x-y
-0.002792527  0.028448867  1.817448093

3.1.1 欧拉角与旋转矩阵

3.1.1.1 欧拉角转旋转矩阵

对于三维坐标空间，以坐标系的三个坐标轴X、Y、Z分别作为旋转轴时，物体实际只在另两坐标轴所在平面上作二维旋转，旋转轴对应的坐标保持不变。因此直接使用二维旋转公式就可推出三维的旋转矩阵。

在二维XOY坐标平面的旋转参见以下博文中的法一：

三种常见矩形框旋转方法推导及其C++实现

最终得到的矩阵形式：

$A'=\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix} \left ( \begin{bmatrix} x\\ y \end{bmatrix}-\begin{bmatrix} c_{x}\\ c_{y} \end{bmatrix} \right )+\begin{bmatrix} c_{x}\\ c_{y} \end{bmatrix} ........ \left ( 3-1 \right )$

式(3-1)中系数矩阵 $\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}$ 即是旋转矩阵R。下文均只考虑旋转，不考虑平移，即取 $\left ( c_{x},c_{y} \right )$ 为坐标原点。借此可推出三维旋转如下：

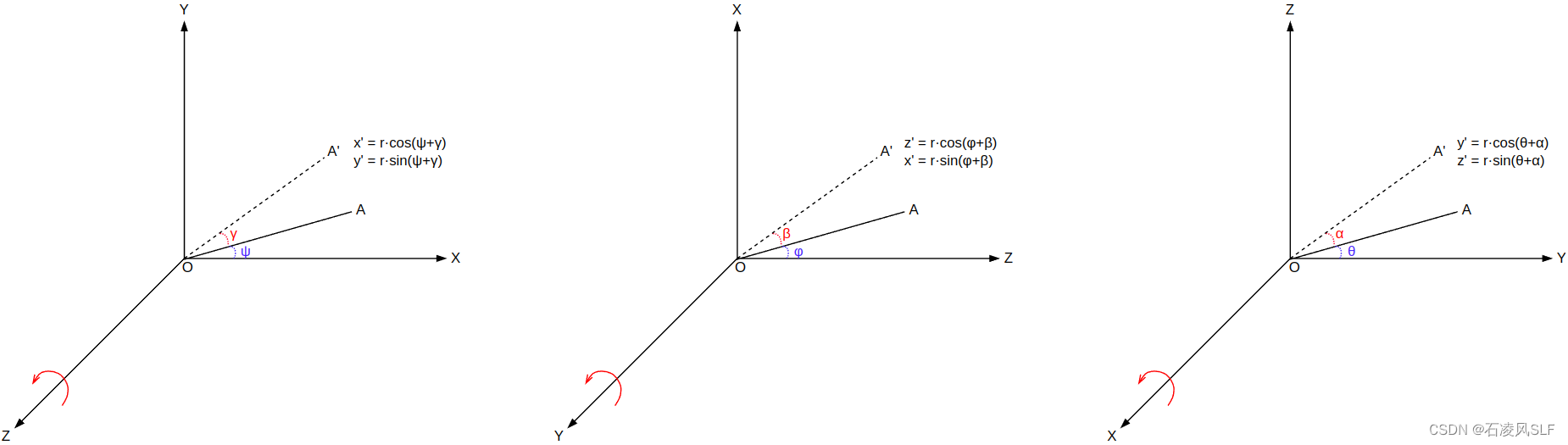
（1）旋转轴为Z轴，旋转角γ

$\begin{bmatrix} x'\\ y'\\z' \end{bmatrix}=\begin{bmatrix} cos\gamma & -sin\gamma & 0 \\ sin\gamma & cos\gamma & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ z \end{bmatrix}=R_{Z}(\gamma) \begin{bmatrix} x\\ y\\ z \end{bmatrix} ........ \left ( 3-2 \right )$

（2）旋转轴为Y轴，旋转角β

$\begin{bmatrix} x'\\ y'\\z' \end{bmatrix}=\begin{bmatrix} cos\beta & 0 & sin\beta \\ 0 & 1 & 0 \\ -sin\beta & 0 & cos\beta \end{bmatrix} \begin{bmatrix} x\\ y\\ z \end{bmatrix}=R_{Y}(\beta) \begin{bmatrix} x\\ y\\ z \end{bmatrix} ........ \left ( 3-3 \right )$

（3）旋转轴为X轴，旋转角α

$\begin{bmatrix} x'\\ y'\\z' \end{bmatrix}=\begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\alpha & -sin\alpha \\ 0 & sin\alpha & cos\alpha \end{bmatrix} \begin{bmatrix} x\\ y\\ z \end{bmatrix}=R_{X}(\alpha) \begin{bmatrix} x\\ y\\ z \end{bmatrix} ........ \left ( 3-4 \right )$

tips: ①绕Y轴旋转时两sinβ的符号与绕X轴和Z轴旋转时相反的原因，是因为按照前述规定的旋转方向，X轴与Z轴组成坐标平面是ZOX顺序，而不是XOZ。

? ? ? ??②观察旋转矩阵 $R_{X}\left ( \alpha \right )$ 、 $R_{Y}\left ( \beta \right )$ 、 $R_{Z}\left ( \gamma \right )$ 中sin量的符号，发现可以巧记为数字1所在行的上一行（或数字1所在列的右侧列）的sin量为正。首行的上一行为末行，最右侧列的右侧列为最左侧列。

由本文1.1节得到的旋转等式 $\vec{a'}=R \vec{a}$ 可知，给旋转前向量左乘旋转矩阵就可得到旋转后的向量。假设使用Z-Y-X旋转顺序，外旋对应的旋转矩阵为：

$R=R_{X}(\alpha) R_{Y}(\beta) R_{Z}(\gamma) \ ........ \left ( 3-5 \right )$

假设使用X-Y-Z旋转顺序，外旋对应的旋转矩阵为：

$R=R_{Z}(\gamma) R_{Y}(\beta) R_{X}(\alpha) \ ........ \left ( 3-6 \right )$

由于内旋效果等价于颠倒顺序后的外旋效果，所以X-Y-Z旋转顺序且内旋所对应的旋转矩阵与式(3-5)一致，Z-Y-X旋转顺序且内旋所对应的旋转矩阵与式(3-6)一致。

tips:?外旋的旋转矩阵，是按照旋转次序，依次左乘各轴分量。内旋的旋转矩阵，是按照旋转次序，依次右乘各轴分量。

//code
{
    Eigen::Matrix3d E2R;
    const double c_gamma = std::cos(gamma), c_alpha = std::cos(alpha), c_beta = std::cos(beta);
    const double s_gamma = std::sin(gamma), s_alpha = std::sin(alpha), s_beta = std::sin(beta);
    Eigen::Matrix3d R_x, R_y, R_z;
    R_x << 1.0, 0.0, 0.0,
           0.0, c_alpha, -s_alpha,
           0.0, s_alpha, c_alpha;
    R_y << c_beta, 0.0, s_beta,
           0.0, 1.0, 0.0,
           -s_beta, 0.0, c_beta;
    R_z << c_gamma, -s_gamma, 0.0,
           s_gamma, c_gamma, 0.0,
           0.0, 0.0, 1.0;
    E2R = R_z*R_x*R_y;
    std::cout << "Euler Angles to Rotation Matrix: " << E2R.determinant() << std::endl << E2R << std::endl << std::endl;
}

//print
Euler Angles to Rotation Matrix: 1.000000000
-0.243982607 -0.969731574 -0.009652007
 0.969362354 -0.244157481  0.026902609
-0.028444919 -0.002792523  0.999591461

前述Tait–Bryan angles定义的六种旋转顺序，对应的旋转矩阵如下图表所示[wiki]。对于Z-Y-X旋转顺序，外旋式(3-5)对应 $X_{1}Y_{2}Z_{3}$ ，内旋式(3-6)对应 $Z_{1}Y_{2}X_{3}$ 。右侧矩阵中的字母加数字表示cos(数字对应轴的转角)、sin(数字对应轴的转角)。

//code
{
    Eigen::Matrix3d E2R;
    const double c1 = std::cos(gamma), c2 = std::cos(alpha), c3 = std::cos(beta);
    const double s1 = std::sin(gamma), s2 = std::sin(alpha), s3 = std::sin(beta);
    E2R <<  c1*c3-s1*s2*s3, -c2*s1, c1*s3+c3*s1*s2,
            c3*s1+c1*s2*s3,  c1*c2, s1*s3-c1*c3*s2,
           -c2*s3,           s2,    c2*c3;
    std::cout << "Euler Angles to Rotation Matrix: " << std::endl << E2R << std::endl << std::endl;
}

//print
Euler Angles to Rotation Matrix: 
-0.243982607 -0.969731574 -0.009652007
 0.969362354 -0.244157481  0.026902609
-0.028444919 -0.002792523  0.999591461

3.1.1.2 旋转矩阵转欧拉角

即根据指定的旋转顺序和内旋或外旋，将各轴的旋转角逆推出来。结合上一节，由于旋转矩阵R的各元素均是由旋转角的正余弦值组成，因此正弦或余弦表示的单项元素直接求反正弦或反余弦；而正余弦共同表示的元素项可两项元素求比例得到正切值，再反正切运算即可得到旋转角值，如下图表所示[wiki]。注意：此处的α、β、γ仅表示每次旋转的转角（即α、β、γ分别对应第一次、第二次、第三次旋转的角度），而与本章节开头所定义的“绕三轴旋转的角度(α,β,γ)，分别对应(x,y,z)三个坐标轴”并无联系。

由以上图表可知，当 $R_{11}$ 、 $R_{22}$ 、 $R_{33}$ 出现等于0时，分式的分母就会为零，且转换本身是非线性的。因此应避免使用该转换方式。

tips: ①R的数字下标指代矩阵元素位置索引，从1开始（非0开始）。

? ? ? ? ②各旋转角有取值范围。比如飞行器的roll、pitch、yaw都定义在[-pi:pi]，而车辆的roll、pitch可定义在[-pi/2:pi/2]。

? ? ? ? ③Eigen库Matrix矩阵的成员函数eulerAngles()的入参顺序和返回值元素顺序均对应旋转轴顺序，且返回值第一元素取值范围为[0:pi]，第二、第三元素取值范围为[-pi:pi]，使用过程需注意，具体参见头文件eigen3/Eigen/src/Geometry/EulerAngles.h。

为何R2E_z_angle计算出来的结果是一个补角？？？

//code
{
    #if 1
    const double c1 = std::cos(gamma), c2 = std::cos(alpha), c3 = std::cos(beta);
    const double s1 = std::sin(gamma), s2 = std::sin(alpha), s3 = std::sin(beta);
    const auto R2E_z_angle = std::atan((c2*s1)/(c1*c2)); //why is supplementary angle ???
    const auto R2E_x_angle = std::asin(s2);
    const auto R2E_y_angle = std::atan((c2*s3)/(c2*c3));
    const Eigen::Vector3d R2E(R2E_x_angle, R2E_y_angle, R2E_z_angle);
    #else
    const Eigen::Vector3d R2E_zxy = E2R.eulerAngles(2, 0, 1); //Note: The first parameter corresponds to the angle range of [0:pi], and the other two are [-pi:pi].
    const Eigen::Vector3d R2E(R2E_zxy(1), R2E_zxy(2), R2E_zxy(0));
    #endif
    std::cout << "Rotation Matrix to Euler Angles: " << std::endl << R2E.transpose() << std::endl << std::endl;
}

//print
Rotation Matrix to Euler Angles: 
-0.002792527  0.028448867  -1.324144561

3.1.2 欧拉角与旋转向量

如本章节开头所述，使用欧拉角必须先进行定义，因为不同定义方式结果不同。本节所使用欧拉角定义为：绕(x,y,z)三轴旋转的角度分别对应为(α,β,γ)、Z-X-Y旋转顺序、内旋。

3.1.2.1 欧拉角转旋转向量

间接法：

① 欧拉角? $\rightarrow$ ?旋转矩阵? $\rightarrow$ ?旋转向量?

② 欧拉角? $\rightarrow$ ?四元数? $\rightarrow$ ?旋转向量，eg.

按照本节开头所定义欧拉角，由本文4.1.3.2节可知欧拉角转四元数的变换关系式，以及由4.1.2.1节可知四元数转旋转向量的变换关系式。分别如下：

$Euler \ to \ Quaternion \rightarrow \left\{\begin{matrix} q_{w}=cos\frac{\gamma }{2}cos\frac{\alpha }{2}cos\frac{\beta }{2}-sin\frac{\gamma }{2}sin\frac{\alpha }{2}sin\frac{\beta }{2} \\ q_{x}=cos\frac{\gamma }{2}sin\frac{\alpha }{2}cos\frac{\beta }{2}-sin\frac{\gamma }{2}cos\frac{\alpha }{2}sin\frac{\beta }{2} \\ q_{y}=cos\frac{\gamma }{2}cos\frac{\alpha }{2}sin\frac{\beta }{2}+sin\frac{\gamma }{2}sin\frac{\alpha }{2}cos\frac{\beta }{2} \\ q_{z}=sin\frac{\gamma }{2}cos\frac{\alpha }{2}cos\frac{\beta }{2}+cos\frac{\gamma }{2}sin\frac{\alpha }{2}sin\frac{\beta }{2} \end{matrix}\right. \\ Quaternion \ to \ Angle \rightarrow \left\{\begin{matrix} \theta=2arccosq_{w} \\ \vec{n} = \begin{bmatrix} q_{x} , q_{y} , q_{z} \end{bmatrix}^{T}/sin\frac{\theta}{2}=\begin{bmatrix} q_{x} , q_{y} , q_{z} \end{bmatrix}^{T}/\sqrt{1-q_{w}^{2}} \end{matrix}\right.$

将上式中四元数的实部和虚部抵消掉（由于 $\begin{bmatrix} q_{x} , q_{y} , q_{z} \end{bmatrix}^{T}/\sqrt{1-q_{w}^{2}}$ 和 $\begin{bmatrix} q_{x} , q_{y} , q_{z} \end{bmatrix}^{T}$ 共线，因此都在旋转轴上，所以计算过程可先省略分母中的\sqrt{1-q_{w}^{2}}。但最终需要得到一个单位向量，所以还需额外再归一化处理），即可得到欧拉角到旋转向量的变换关系式：

$\left\{\begin{matrix} \theta=2arccos(cos\frac{\gamma }{2}cos\frac{\alpha }{2}cos\frac{\beta }{2}-sin\frac{\gamma }{2}sin\frac{\alpha }{2}sin\frac{\beta }{2}) \\ \vec{n} = \begin{bmatrix} cos\frac{\gamma }{2}sin\frac{\alpha }{2}cos\frac{\beta }{2}-sin\frac{\gamma }{2}cos\frac{\alpha }{2}sin\frac{\beta }{2} , cos\frac{\gamma }{2}cos\frac{\alpha }{2}sin\frac{\beta }{2}+sin\frac{\gamma }{2}sin\frac{\alpha }{2}cos\frac{\beta }{2} , sin\frac{\gamma }{2}cos\frac{\alpha }{2}cos\frac{\beta }{2}+cos\frac{\gamma }{2}sin\frac{\alpha }{2}sin\frac{\beta }{2} \end{bmatrix}^{T} / \sqrt{(cos\frac{\gamma }{2}sin\frac{\alpha }{2}cos\frac{\beta }{2}-sin\frac{\gamma }{2}cos\frac{\alpha }{2}sin\frac{\beta }{2})^{2} +(cos\frac{\gamma }{2}cos\frac{\alpha }{2}sin\frac{\beta }{2}+sin\frac{\gamma }{2}sin\frac{\alpha }{2}cos\frac{\beta }{2})^{2} +(sin\frac{\gamma }{2}cos\frac{\alpha }{2}cos\frac{\beta }{2}+cos\frac{\gamma }{2}sin\frac{\alpha }{2}sin\frac{\beta }{2} )^{2} } \end{matrix}\right.$

直接法：

将绕三轴旋转的欧拉角(α,β,γ)作为旋转角，坐标轴作为旋转轴，并在轴上分别取单位向量 $\vec{n}_{x}=(1,0,0)$ 、 $\vec{n}_{y}=(0,1,0)$ 、 $\vec{n}_{z}=(0,0,1)$ ，即构成三个旋转向量，然后按照旋转顺序依次乘上各旋转轴对应的旋转向量即可得最终的旋转向量 $\left ( \theta \vec{n} \right )$ ，即：

$(\theta \vec{n})=(\gamma \vec{n}_{z})(\alpha \vec{n}_{x})(\beta \vec{n}_{y})$ ? //非严格意义的向量乘

//code
{
    Eigen::AngleAxisd E2V(Eigen::AngleAxisd(gamma, Eigen::Vector3d::UnitZ()) *
                          Eigen::AngleAxisd(alpha, Eigen::Vector3d::UnitX()) *
                          Eigen::AngleAxisd(beta, Eigen::Vector3d::UnitY())); 
    std::cout << "Euler Angles to Axis-Angle: " << E2V.axis().norm() << std::endl << "angle=" << E2V.angle() << ", axis=" << E2V.axis().transpose() << std::endl << std::endl;
}

//print
Euler Angles to Axis-Angle: 1.000000000
angle=1.817567592, axis=-0.015311407  0.009690003  0.999835819

3.1.2.2 旋转向量转欧拉角

间接法：

① 旋转向量? $\rightarrow$ ?旋转矩阵? $\rightarrow$ ?欧拉角

//code
{
    const auto V2E_zxy = V2R.eulerAngles(2, 0, 1);
    const Eigen::Vector3d V2E(V2E_zxy(1), V2E_zxy(2), V2E_zxy(0));
    std::cout << "Axis-Angle to Euler Angles: " << std::endl << V2E.transpose() << std::endl << std::endl;
}

//print
Axis-Angle to Euler Angles: 
-0.002792527  0.028448866  1.817448093

② 旋转向量? $\rightarrow$ ?四元数? $\rightarrow$ ?欧拉角，eg.

按照本节开头所定义欧拉角，由本文4.1.3.1节可知四元数转欧拉角的变换关系式，以及由4.1.2.2节可知旋转向量转四元数的变换关系式。分别如下：

$Quaternion \ to \ Euler \rightarrow \left\{\begin{matrix} \angle Z =arctan(\frac{-(2q_{x}q_{y}-2q_{w}q_{z})}{q_{w}^{2}-q_{x}^{2}+q_{y}^{2}-q_{z}^{2}}) \\ \angle X = arcsin(2q_{y}q_{z}+2q_{w}q_{x}) \\ \angle Y = arctan(\frac{-(2q_{x}q_{z}-2q_{w}q_{y})}{q_{w}^{2}-q_{x}^{2}-q_{y}^{2}+q_{z}^{2}}) \end{matrix}\right. \\ Angle \ to \ Quaternion \rightarrow \left\{\begin{matrix} q_{w}=cos\frac{\theta}{2} \\ \begin{bmatrix} q_{x} , q_{y} , q_{z} \end{bmatrix}^{T} = sin\frac{\theta}{2} \begin{bmatrix} n_{x} , n_{y} , n_{z} \end{bmatrix}^{T} \end{matrix}\right.$

将上式中四元数的实部和虚部抵消掉，即可得到旋转向量到欧拉角的变换关系式：

$\angle Z =arctan(\frac{-(2q_{x}q_{y}-2q_{w}q_{z})}{q_{w}^{2}-q_{x}^{2}+q_{y}^{2}-q_{z}^{2}}) \\ = arctan(\frac{2q_{w}q_{z}-2q_{x}q_{y}}{2(q_{w}^{2}+q_{y}^{2})-1}) \\ = arctan(\frac{2n_{z}cos\frac{\theta }{2}sin\frac{\theta }{2}-2n_{x}n_{y}sin^{2}\frac{\theta }{2}}{2[cos^{2}\frac{\theta }{2}+(n_{y}sin\frac{\theta }{2})^{2}]-1}) \\ =arctan(\frac{n_{z}sin\theta -n_{x}n_{y}(1-cos\theta )}{cos\theta +n_{y}^{2}(1-cos\theta )}) \\ \angle X = arcsin(2q_{y}q_{z}+2q_{w}q_{x}) \\ = arcsin(2n_{y}n_{z}sin^{2}\frac{\theta }{2} + 2n_{x}cos\frac{\theta }{2}sin\frac{\theta }{2}) \\ =arcsin(n_{x}sin\theta +n_{y}n_{z}(1-cos\theta ))\\ \angle Y = arctan(\frac{-(2q_{x}q_{z}-2q_{w}q_{y})}{q_{w}^{2}-q_{x}^{2}-q_{y}^{2}+q_{z}^{2}}) \\ =arctan(\frac{2q_{w}q_{y}-2q_{x}q_{z}}{2(q_{w}^{2}+q_{z}^{2})-1}) \\ = arctan(\frac{2n_{y}cos\frac{\theta }{2}sin\frac{\theta }{2}-2n_{x}n_{z}sin^{2}\frac{\theta }{2}}{2[cos^{2}\frac{\theta }{2}+(n_{z}sin\frac{\theta }{2})^{2}]-1}) \\ =arctan(\frac{n_{y}sin\theta -n_{x}n_{z}(1-cos\theta )}{cos\theta +n_{z}^{2}(1-cos\theta )})$

为何V2E_z_angle计算出来的结果是一个补角？？？

//code
{
    const auto c_theta = std::cos(angle), s_theta = std::sin(angle);
    const auto V2E_z_angle = std::atan((axis(2)*s_theta-axis(0)*axis(1)*(1-c_theta))/(c_theta+std::pow(axis(1),2)*(1-c_theta))); //why is supplementary angle ???
    const auto V2E_x_angle = std::asin(axis(0)*s_theta+axis(1)*axis(2)*(1-c_theta));
    const auto V2E_y_angle = std::atan((axis(1)*s_theta-axis(0)*axis(2)*(1-c_theta))/(c_theta+std::pow(axis(2),2)*(1-c_theta)));
    const Eigen::Vector3d V2E(V2E_x_angle, V2E_y_angle, V2E_z_angle);
    std::cout << "Axis-Angle to Euler Angles: " << std::endl << V2E.transpose() << std::endl << std::endl;
}

//print
Axis-Angle to Euler Angles: 
-0.002792527  0.028448866 -1.324144561

3.2 欧拉角的缺陷

使用欧拉角表示旋转时，当绕pitch角对应轴的旋转为第二次旋转，且第二次旋转的旋转角度为±90°时，就会导致第一次旋转与第三次旋转的旋转轴共线，也就是出现万向锁现象（奇异性问题）。比如下图（pitch角对应Y轴），第一次旋转与第三次旋转的旋转轴共线，使得系统丢失了一个自由度。

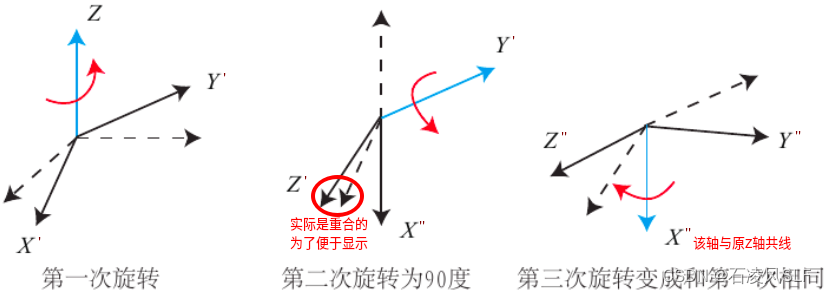
举个实际的栗子，针对3.1.1.1节图表中 $Z_{1}Y_{2}X_{3}$ （pitch角对应Y轴）和 $Y_{1}X_{2}Z_{3}$ （pitch角对应X轴），若第二次旋转的旋转角度为90°，则对应式变为：

$Z_{1}Y_{2}X_{3}=\begin{bmatrix} 0 & c_{1}s_{3}-c_{3}s_{1} & s_{1}s_{3}+c_{1}c_{3} \\ 0 & c_{1}c_{3}+s_{1}s_{3} & c_{3}s_{1}-c_{1}s_{3} \\ -1 & 0 & 0 \end{bmatrix}$ ?， $Y_{1}X_{2}Z_{3}=\begin{bmatrix} c_{1}c_{3}+s_{1}s_{3} & c_{3}s_{1}-c_{1}s_{3} & 0 \\ 0 & 0 & -1 \\ c_{1}s_{3}-c_{3}s_{1} & c_{1}c_{3}+s_{1}s_{3} & 0 \end{bmatrix}$

此时，旋转自由度降到两自由度，需通过调整旋转顺序或使用四元数等旋转方法进行规避。

四、四元数

如前所述，在表示旋转时欧拉角和旋转向量虽然相较旋转矩阵更紧凑，但二者均具有奇异性。本节将讲述如何用四元数表示旋转，其表达方式既紧凑（仅需存储4个浮点数）、又无歧义性。且无论是求逆、串联等操作，相比矩阵更加高效。

在正式谈论四元数前，先回顾一下空间的概念：一般而言高维空间都存在低维子空间，比如二维空间中的一维子空间（直线），三维空间中的二维子空间（面）和一维子空间。对于四维空间，很难直观想象，但其必存在三维子空间以及其它低维子空间。将四维空间用(w,x,y,z)表示，当w=0时，(0,x,y,z)就是一个三维子空间，所以三维空间向量是可以映射到四维的三维子空间的。基于此才有下文单位四元数可对三维向量进行旋转操作，因为旋转后的向量存在于四维的三维子空间中，因而可以映射回三维空间。

实际上四元数的很多特性都是从低维空间拓展而来，更具体的说是从复数这一概念拓展的。用复数可以表示二维旋转[博文中法三]，那么用三个数字（三元数）是否就可以表示三维空间中的旋转呢？事实上并不可以，要表示三维空间中的旋转得使用四元数（四个维度的超复数）。

4.1 定义和推导

在平面直角坐标系中复数包含两个相互垂直的轴（实轴和虚轴），那么是否只要再加上一个虚轴，构造一个三维的超复数，就能像复数相乘可描述二维旋转一样，用此超复数描述三维空间中的旋转呢？按照这个思路，定义如下表达式：

$z=a+ib+jc$

在复数中虚数单位记为 $i=(0,1)$ ，并有 $i \times i=(0,1) \times (0,1)=(-1,0)=-1$ 。对于同样作为虚数单位的 $j$ ，应同样满足 $j^{2}=-1$ 。

接下来的问题是 $ij$ 的结果是什么？

假设 $ij=1$ ，该等式两边同时左乘 $i$ ，得到 $-j=i$ ，假设不成立；

假设 $ij=-1$ ，该等式两边同时左乘 $i$ ，得到 $-j=-i$ ，假设不成立；

假设 $ij=i$ ，该等式两边同时左乘 $i$ ，得到 $-j=-1$ ，假设不成立；

假设 $ij=j$ ，该等式两边同时右乘 $j$ ，得到 $-i=-1$ ，假设不成立。

显然给 $ij$ 左乘 $i$ 还是右乘 $j$ 都不能正确表示 $ij$ 的结果。这似乎表明所构造的三个维度的超复数并不能够描述三维空间中的旋转，事实上确实如此。既然行不通，那就尝试用四个维度的超复数，也就是四元数。定义如下：

$z=a+ib+jc+kd$

把 $i,j,k$ 看成三个坐标轴，相互之间的乘法参照外积，并且符号遵循右手法则，不难得到以下等式：

$\left\{\begin{matrix} i^{2}=j^{2}=k^{2}=-1 \\ ij=k, \ ji=-k \\ jk=i, \ kj=-i \\ ki=j, \ ik=-j \\ ijk=-1 \end{matrix}\right.$

在复数中，乘以i会发生旋转90°，那么对于四个维度的超复数，是否也是这样？比如对于 $ij=k$ ，是否意味着绕 $k$ 轴旋转90°，与先绕 $i$ 轴旋转90°再绕 $j$ 轴旋转90°的效果一致？从下图看来仍按照复数的90°旋转， $ij=k$ 这个等式并不成立。

事实上想让 $i,j,k$ 相互之间的乘法等式成立，每次必须是旋转180°，见下图：

对于等式 $i^{2}=j^{2}=k^{2}=-1$ ，意味着绕各轴旋转360°后会得到一个相反的东东（对于复数来说是绕平面旋转180°）。

用四元数表示三维旋转，如本章开头所述，可将三维空间中的待旋转向量映射到四维的三维子空间中，此时三个虚轴对应空间的三个维度，其值是向量在三个坐标轴的投影，实轴的值是0。在四元数中称此为纯虚四元数（对应复数中纯虚数）。即三维空间中一点 $a=\left ( x,y,z \right )$ 映射到四维的三维子空间中后可用纯虚四元数表示为：

$\textit{\textbf{a}}=0+ix+jy+kz$

参照复数表示旋转，由于旋转不会改变大小，为了简化计算，同样取单位长度的四元数。其定义和具有的性质如下：

$\left\{\begin{matrix} \textit{\textbf{q}} = q_{w}+iq_{x}+jq_{y}+kq_{z} \\ \bar{\textit{\textbf{q}}} = q_{w}-iq_{x}-jq_{y}-kq_{z} \\ \textit{\textbf{q}}^{-1} = \bar{\textit{\textbf{q}}} / ||\textit{\textbf{q}}||^{2} \\ ||\textit{\textbf{q}}|| = \sqrt{q_{w}^{2}+q_{x}^{2}+q_{y}^{2}+q_{z}^{2}} = 1 , \ s.t. \\ \textit{\textbf{q}}^{-1} = \bar{\textit{\textbf{q}}} \end{matrix}\right.$

而用单位四元数描述三维旋转的表达式为：

${\textit{\textbf{a}}}' = \textit{\textbf{q}} \textit{\textbf{a}} \bar{\textit{\textbf{q}}}=\textit{\textbf{q}} \textit{\textbf{a}} \textit{\textbf{q}}^{-1} ......\left ( 4-1 \right )$

式(4-1)的乘法均为四元数乘法，其结果仍是四元数，并且为纯虚四元数（因为将三维向量映射到四维还得映射回去，那么纯虚四元数是必须的，如果脱离这个三维子空间，映射关系就变了）。将结果的虚部取出来即可得旋转后的点坐标。

//code
{
    const double qw = 0.614705493, qx = -0.012076975, qy = 0.007643055, qz = 0.788627217;
    // const Eigen::Quaterniond(Eigen::Vector4d(qx,qy,qz,qw));
    const Eigen::Quaterniond Q(qw, qx, qy, qz);
    std::cout << "Quaternion: " << Q.squaredNorm() << std::endl << Q.coeffs().transpose() << std::endl << std::endl;
    std::cout << Q.x() << "  " << Q.y() << "  " << Q.z() << "  " << Q.w() << std::endl << std::endl;
    std::cout << "(1.0, 2.0, 3.0) after rotation (by quaternion): " << std::endl << (Q*a).transpose() << std::endl << std::endl; //overloaded operator
    std::cout << "(1.0, 2.0, 3.0) after rotation (by quaternion): " << std::endl << (Q*Eigen::Quaterniond(0,a(0),a(1),a(2))*Q.inverse()).coeffs().transpose() << std::endl << std::endl;
}

//print
Quaternion: 1.000000000
-0.012076975  0.007643055  0.788627217  0.614705493

-0.012076975  0.007643055  0.788627217  0.614705493

(1.0, 2.0, 3.0) after rotation (by quaternion): 
-2.212401776  0.561755216  2.964744417

(1.0, 2.0, 3.0) after rotation (by quaternion): 
-2.212401776  0.561755216  2.964744417 -0.000000000

回顾旋转矩阵和旋转向量描述旋转的表达式，式(4-1)中为什么 $\textit{\textbf{a}}$ 左乘 $\textit{\textbf{q}}$ 后还要右乘 $\textit{\textbf{q}}$ 对应的逆或者共轭呢？可以阅读[文章倒数第二和第三章节]或许可以找到答案。本文3.1.1.1节中根据欧拉角旋转顺序不同各轴旋转矩阵相乘顺序不同或许也可从中找到答案。

4.1.1 四元数与旋转矩阵

将四元数的实部用一个标量s表示（s与 $q_{w}$ 均表示实部，根据具体的场合自由切换使用），三个虚部构成的向量用 $\vec{v}$ 表示，即：

$\textit{\textbf{q}}=q_{w}+iq_{x}+jq_{y}+kq_{z}=\begin{bmatrix} s, \vec{v} \end{bmatrix}^{T}, \ s=q_{w}, \ \vec{v}=\begin{bmatrix} q_{x},q_{y},q_{z} \end{bmatrix}^{T}$

定义如下两个四元数：

$\left\{\begin{matrix} \textit{\textbf{q}}_{a} = s_{a}+ix_{a}+jy_{a}+kz_{a}\\ \textit{\textbf{q}}_{b} = s_{b}+ix_{b}+jy_{b}+kz_{b} \end{matrix}\right.$

计算两个四元数的乘积，可得：

用向量的形式表示为（外积的存在证明四元数乘法一般不满足交换律）：

$\textit{\textbf{q}}_{a}\textit{\textbf{q}}_{b}= \begin{bmatrix} s_{a}s_{b}-\vec{v}_{a}^{T}\vec{v}_{b} , s_{a}\vec{v}_{b}+s_{b}\vec{v}_{a}+\vec{v}_{a}\times \vec{v}_{b} \end{bmatrix}^{T}$

借助2.1.1节提及的反对称矩阵可将两个定义在同一个坐标系的向量的叉积运算转换为矩阵和向量的乘法运算，即 $\left ( \vec{a} \times \vec{b}\right )\rightarrow (\vec{a}^{\wedge} \vec{b})=-\left ( \vec{b}^{\wedge} \vec{a} \right )$ ，可得矩阵表示形式为：

$\textit{\textbf{q}}_{a}\textit{\textbf{q}}_{b}= \begin{bmatrix} s_{a} & -\vec{v}_{a}^{T} \\ \vec{v}_{a} & s_{a}I+\vec{v}_{a}^{\wedge} \end{bmatrix} \begin{bmatrix} s_{b} \\ \vec{v}_{b} \end{bmatrix} = \begin{bmatrix} s_{b} & -\vec{v}_{b}^{T} \\ \vec{v}_{b} & s_{b}I-\vec{v}_{b}^{\wedge} \end{bmatrix} \begin{bmatrix} s_{a} \\ \vec{v}_{a} \end{bmatrix}........\left ( 4-2 \right )$

基于上式中出现的两矩阵，定义以下两个符号运算与之对应：

$\textit{\textbf{q}}^{+}=\begin{bmatrix} s & -\vec{v}^{T} \\ \vec{v} & sI+\vec{v}^{\wedge} \end{bmatrix} \\ \textit{\textbf{q}}^{\oplus}=\begin{bmatrix} s & -\vec{v}^{T} \\ \vec{v} & sI-\vec{v}^{\wedge} \end{bmatrix}, \ \bar{\textit{\textbf{q}}}^{\oplus }=\begin{bmatrix} s & \vec{v}^{T} \\ -\vec{v} & sI+\vec{v}^{\wedge} \end{bmatrix}........\left ( 4-3 \right )$

所以式(4-2)可直接表示为：

$\textit{\textbf{q}}_{a} \textit{\textbf{q}}_{b}= \textit{\textbf{q}}_{a}^{+}\textit{\textbf{q}}_{b} = \textit{\textbf{q}}_{b}^{\oplus }\textit{\textbf{q}}_{a}........\left ( 4-4 \right )$

4.1.1.1 四元数转旋转矩阵

由式(4-1)和式(4-4)有：

${\textit{\textbf{a}}}' = \textit{\textbf{q}} \textit{\textbf{a}} \bar{\textit{\textbf{q}}} =\textit{\textbf{q}}^{+} \textit{\textbf{a}} \bar{\textit{\textbf{q}}} =\textit{\textbf{q}}^{+} \bar{\textit{\textbf{q}}}^{\oplus } \textit{\textbf{a}} \ ........\left ( 4-5 \right )$

将式(4-3)所定义符号运算代入 $\textit{\textbf{q}}^{+} \bar{\textit{\textbf{q}}}^{\oplus }$ 中并展开可得到：

$\textit{\textbf{q}}^{+} \bar{\textit{\textbf{q}}}^{\oplus } =\begin{bmatrix} s & -\vec{v}^{T} \\ \vec{v} & sI+\vec{v}^{\wedge} \end{bmatrix} \begin{bmatrix} s & \vec{v}^{T} \\ -\vec{v} & sI+\vec{v}^{\wedge} \end{bmatrix} \\ =\begin{bmatrix} 1 & \vec{0}^{T}\\ \vec{0} & \vec{v}\vec{v}^{T}+s^{2}I+2s\vec{v}^{\wedge} +\left ( \vec{v}^{\wedge} \right )^{2} \end{bmatrix}$

将上式代入式(4-5)中有：

${\textit{\textbf{a}}}' =\textit{\textbf{q}}^{+} \bar{\textit{\textbf{q}}}^{\oplus } \textit{\textbf{a}} \\ =\begin{bmatrix} 1 & \vec{0}^{T}\\ \vec{0} & \vec{v}\vec{v}^{T}+s^{2}I+2s\vec{v}^{\wedge} +\left ( \vec{v}^{\wedge} \right )^{2} \end{bmatrix}\begin{bmatrix} s_{a}\\ \vec{v}_{a} \end{bmatrix} \\ =\begin{bmatrix} s_{a}\\ (\vec{v}\vec{v}^{T}+s^{2}I+2s\vec{v}^{\wedge} +\left ( \vec{v}^{\wedge} \right )^{2})\vec{v}_{a} \end{bmatrix}........\left ( 4-6 \right )$

因为 $\textit{\textbf{a}}$ 和 ${\textit{\textbf{a}}}'$ 都是纯虚四元数（ $s_{a}=0$ ），由本文1.1节等式 $\vec{a'}=R \vec{a}$ 可知，式(4-6)右下角部分即为旋转矩阵R。所以四元数到旋转矩阵的变换关系式为：

$R=\vec{v}\vec{v}^{T}+s^{2}I+2s\vec{v}^{\wedge} +\left ( \vec{v}^{\wedge} \right )^{2} \\ =\begin{bmatrix} q_{w}^{2}+q_{x}^{2}-q_{y}^{2}-q_{z}^{2} & 2q_{x}q_{y}-2q_{w}q_{z} & 2q_{x}q_{z}+2q_{w}q_{y} \\ 2q_{x}q_{y}+2q_{w}q_{z} & q_{w}^{2}-q_{x}^{2}+q_{y}^{2}-q_{z}^{2} & 2q_{y}q_{z}-2q_{w}q_{x} \\ 2q_{x}q_{z}-2q_{w}q_{y} & 2q_{y}q_{z}+2q_{w}q_{x} & q_{w}^{2}-q_{x}^{2}-q_{y}^{2}+q_{z}^{2} \end{bmatrix}........\left ( 4-7 \right )$

//code
{
    const auto Q2R = Q.toRotationMatrix(); //Q.matrix() == Q.toRotationMatrix()
    std::cout << "Quaternion to Rotation Matrix: " << Q2R.determinant() << std::endl << Q2R << std::endl << std::endl;
}

//print
Quaternion to Rotation Matrix: 1.000000000
-0.243982607 -0.969731574 -0.009652007
 0.969362354 -0.244157481  0.026902608
-0.028444918 -0.002792523  0.999591461

4.1.1.2 旋转矩阵转四元数

定义一个一般形式的旋转矩阵：

$R=\begin{bmatrix} R_{11} & R_{12} & R_{13}\\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{bmatrix}........\left ( 4-8 \right )$

对上一节式(4-7)和本节式(4-8)两边同时求迹：

$\left\{\begin{matrix} tr(R) =4q_{w}^{2}-1, \ see \ section \ 4.1.2.1 \\ tr(R)=R_{11}+R_{22}+R_{33} \end{matrix}\right.$

由上式可得四元数的实部：

$q_{w} =\frac{\sqrt{R_{11}+R_{22}+R_{33}+1}}{2}$

观察式(4-7)所列旋转矩阵，关于主对角线对称的两元素，均存在相同项，因此将该矩阵中这几个元素与式(4-8)所列矩阵对应匹配上，就可以抵消掉该相同项，而 $q_{w}$ 目前已知，所以剩余的那项（四元数的虚部）就可换算得到。

$\left\{\begin{matrix} R_{21}=2q_{x}q_{y}+2q_{w}q_{z}, \ R_{12}=2q_{x}q_{y}-2q_{w}q_{z} \\ R_{31}=2q_{x}q_{z}-2q_{w}q_{y}, \ R_{13}=2q_{x}q_{z}+2q_{w}q_{y} \\ R_{32}=2q_{y}q_{z}+2q_{w}q_{x}, \ R_{23}=2q_{y}q_{z}-2q_{w}q_{x} \\ \end{matrix}\right.$

将上式化简后就可得到旋转矩阵到四元数的变换关系式：

$\left\{\begin{matrix} q_{z}=\frac{R_{21}-R_{12}}{4q_{w}} \\ q_{y}=\frac{R_{13}-R_{31}}{4q_{w}} \\ q_{x}=\frac{R_{32}-R_{23}}{4q_{w}} \\ q_{w} =\frac{\sqrt{R_{11}+R_{22}+R_{33}+1}}{2} \end{matrix}\right. \ ........\left ( 4-9 \right )$

//code
{
    const double R2Q_qw = 0.5*std::sqrt(1.0+R(0,0)+R(1,1)+R(2,2));
    const double R2Q_qx = (R(2,1)-R(1,2))/(4*R2Q_qw);
    const double R2Q_qy = (R(0,2)-R(2,0))/(4*R2Q_qw);
    const double R2Q_qz = (R(1,0)-R(0,1))/(4*R2Q_qw);
    const Eigen::Quaterniond R2Q(R2Q_qw, R2Q_qx, R2Q_qy, R2Q_qz);
    // const Eigen::Quaterniond R2Q(R);
    // Eigen::Quaterniond R2Q;
    // R2Q = R; //overloaded operator
    std::cout << "Rotation Matrix to Quaternion: " << R2Q.squaredNorm() << std::endl << R2Q.coeffs().transpose() << std::endl << std::endl;
}

//print
Rotation Matrix to Quaternion: 0.999999999
-0.012076975  0.007643055  0.788627217  0.614705493

4.1.2?四元数与旋转向量

4.1.2.1 四元数转旋转向量

参照2.1.2节旋转矩阵转旋转向量，对4.1.1.1节式(4-7)两边同时求迹：

$tr(R) =tr(\vec{v}\vec{v}^{T}+s^{2}I+2s\vec{v}^{\wedge} +\left ( \vec{v}^{\wedge} \right )^{2}) \\ =(q_{w}^{2}+q_{x}^{2}-q_{y}^{2}-q_{z}^{2})+(q_{w}^{2}-q_{x}^{2}+q_{y}^{2}-q_{z}^{2})+(q_{w}^{2}-q_{x}^{2}-q_{y}^{2}+q_{z}^{2}) \\ =3q_{w}^{2}-q_{x}^{2}-q_{y}^{2}-q_{z}^{2} \\ =4q_{w}^{2}-1$

由2.1.2节可知 $\theta=arccos\frac{tr(R)-1}{2}$ ，将上式代入其中可得：

$\theta=arccos\frac{tr(R)-1}{2} =arccos\frac{(4q_{w}^{2}-1)-1}{2} =arccos(2q_{w}^{2}-1), \ s.t. \\ cos\theta=2q_{w}^{2}-1$

根据三角函数恒等变形公式：

$cos\theta=cos^{2}\frac{\theta}{2}-sin^{2}\frac{\theta}{2} =2cos^{2}\frac{\theta}{2}-1$

综合以上两式可得：

$q_{w}=cos\frac{\theta}{2}, \ s.t. \\ \theta=2arccosq_{w}$

接下来如何确定旋转轴呢？假设 $\textit{\textbf{a}}$ 的虚部与单位旋转四元数 $\textit{\textbf{q}}$ 的虚部一致，此时回到4.1.1.1节式(4-6)有：

${\textit{\textbf{a}}}' =\textit{\textbf{q}}^{+} \bar{\textit{\textbf{q}}}^{\oplus } \textit{\textbf{a}} \\ =\begin{bmatrix} 1 & \vec{0}^{T}\\ \vec{0} & \vec{v}\vec{v}^{T}+s^{2}I+2s\vec{v}^{\wedge} +\left ( \vec{v}^{\wedge} \right )^{2} \end{bmatrix}\begin{bmatrix} s_{a}\\ \vec{v} \end{bmatrix} \\ =\begin{bmatrix} s_{a}\\ (\vec{v}\vec{v}^{T}+s^{2}I+2s\vec{v}^{\wedge} +\left ( \vec{v}^{\wedge} \right )^{2})\vec{v} \end{bmatrix} \\ =\begin{bmatrix} s_{a}\\ \vec{v}\vec{v}^{T}\vec{v}+s^{2}\vec{v} \end{bmatrix}$

其中 $(\vec{v}\vec{v}^{T}\vec{v}+s^{2}\vec{v})$ 可进一步化简为：

$\vec{v}\vec{v}^{T}\vec{v}+s^{2}\vec{v}= \begin{bmatrix} q_{x}(q_{x}^{2}+q_{y}^{2}+q_{z}^{2}) \\ q_{y}(q_{x}^{2}+q_{y}^{2}+q_{z}^{2}) \\ q_{z}(q_{x}^{2}+q_{y}^{2}+q_{z}^{2}) \end{bmatrix} +s^{2}\vec{v} =(1-s^{2})\vec{v}+s^{2}\vec{v} =\vec{v}$

显然由 $\textit{\textbf{q}}$ 的虚部组成的向量 $\vec{v}$ 在旋转时是不动的，因此可以将其归一化后的单位向量作为旋转轴。而其模长为：

$\sqrt{q_{x}^{2}+q_{y}^{2}+q_{z}^{2}}=\sqrt{1-q_{w}^{2}}=\sqrt{1-cos^{2}\frac{\theta}{2}}=\sqrt{sin^{2}\frac{\theta}{2}}=sin\frac{\theta}{2}$

所以四元数到旋转向量的变换关系式为：

$\left\{\begin{matrix} \theta=2arccosq_{w} \\ \vec{n} = \begin{bmatrix} q_{x} , q_{y} , q_{z} \end{bmatrix}^{T}/sin\frac{\theta}{2}=\begin{bmatrix} q_{x} , q_{y} , q_{z} \end{bmatrix}^{T}/\sqrt{1-q_{w}^{2}} \end{matrix}\right. \ ........\left ( 4-10 \right )$

上式分母中存在 $sin\frac{\theta }{2}$ ，所以当 $\theta =0^{\circ}$ 时出现除零。此外，当 $\theta =180^{\circ}$ 时会使 $q_{w}=0$ ，四元数退化为三元数。因此应提前识别进行预防。

//code
{
    const Eigen::AngleAxisd Q2V(2.0*std::acos(qw), Eigen::Vector3d(qx,qy,qz)/std::sqrt(1.0-std::pow(qw,2)));
    // const Eigen::AngleAxisd Q2V(Q);
    // Eigen::AngleAxisd Q2V;
    // Q2V = Q; //overloaded operator
    std::cout << "Quaternion to Axis-Angle: " << Q2V.axis().norm() << std::endl << "angle=" << Q2V.angle() << ", axis="  << Q2V.axis().transpose() << std::endl << std::endl;
}

//print
Quaternion to Axis-Angle: 1.000000000
angle=1.817567592, axis=-0.015311407  0.009690003  0.999835819

4.1.2.2 旋转向量转四元数

只需将上一节式(4-10)倒过来即可得到旋转向量到四元数的变换关系式：

$\left\{\begin{matrix} q_{w}=cos\frac{\theta}{2} \\ \begin{bmatrix} q_{x} , q_{y} , q_{z} \end{bmatrix}^{T} = sin\frac{\theta}{2} \begin{bmatrix} n_{x} , n_{y} , n_{z} \end{bmatrix}^{T} \end{matrix}\right. \ ........\left ( 4-11 \right )$

//code
{
    const auto qxyz = std::sin(0.5*angle) * axis;
    Eigen::Quaterniond V2Q(std::cos(0.5*angle), qxyz(0), qxyz(1), qxyz(2));
    // const Eigen::Quaterniond V2Q(V);
    // Eigen::Quaterniond V2Q;
    // V2Q = V; //overloaded operator
    std::cout << "Axis-Angle to Quaternion: " << V2Q.squaredNorm() << std::endl << V2Q.coeffs().transpose() << std::endl << std::endl;
}

//print
Axis-Angle to Quaternion: 1.000000000
-0.012076975  0.007643055  0.788627217  0.614705493

4.1.3 四元数与欧拉角

如本文3.1节所述，使用欧拉角必须先进行定义，因为不同定义方式结果不同。本节所使用欧拉角定义为：绕(x,y,z)三轴旋转的角度分别对应为(α,β,γ)、Z-X-Y旋转顺序、内旋。

4.1.3.1 四元数转欧拉角

间接法：

① 四元数? $\rightarrow$ ?旋转矩阵? $\rightarrow$ ?欧拉角

//code
{
    const Eigen::Vector3d Q2E_zxy = Q.matrix().eulerAngles(2, 0, 1);
    const Eigen::Vector3d Q2E(Q2E_zxy(1), Q2E_zxy(2), Q2E_zxy(0));
    std::cout << "Quaternion to Euler Angles: " << std::endl << Q2E.transpose() << std::endl << std::endl;
}

//print
Quaternion to Euler Angles: 
-0.002792527  0.028448866  1.817448093

② 四元数? $\rightarrow$ ?旋转向量? $\rightarrow$ ?欧拉角?

直接法：

本文4.1.1.1节式(4-7)已给出四元数到旋转矩阵的变换关系，那么四元数到欧拉角的变换就可通过该旋转矩阵间接得到。举个栗子：

本文3.1.1.1节和3.1.1.2节末分别以图表的形式给出了各欧拉角与旋转矩阵之间的变换关系式，对于本节所定义欧拉角，对应的变换关系式分别如下：

将式(4-7)对应的各矩阵元素代入上图各角度计算公式中可得：

$\left\{\begin{matrix} \angle Z =arctan(\frac{-(2q_{x}q_{y}-2q_{w}q_{z})}{q_{w}^{2}-q_{x}^{2}+q_{y}^{2}-q_{z}^{2}}) \\ \angle X = arcsin(2q_{y}q_{z}+2q_{w}q_{x}) \\ \angle Y = arctan(\frac{-(2q_{x}q_{z}-2q_{w}q_{y})}{q_{w}^{2}-q_{x}^{2}-q_{y}^{2}+q_{z}^{2}}) \end{matrix}\right.$

由于旋转矩阵到旋转向量的变换关系式存在分母为零情况，导致上式同样存在。

为何Q2E_z_angle计算出来的结果是一个补角？？？

//code
{
    const auto qw2 = std::pow(qw,2);
    const auto qx2 = std::pow(qx,2);
    const auto qy2 = std::pow(qy,2);
    const auto qz2 = std::pow(qz,2);
    const auto Q2E_z_angle = std::atan((2.0*qw*qz-2.0*qx*qy)/(qw2-qx2+qy2-qz2)); //why is supplementary angle ???
    const auto Q2E_x_angle = std::asin(2.0*qy*qz+2.0*qw*qx);
    const auto Q2E_y_angle = std::atan((2.0*qw*qy-2.0*qx*qz)/(qw2-qx2-qy2+qz2));
    const Eigen::Vector3d Q2E(Q2E_x_angle, Q2E_y_angle, Q2E_z_angle);
    std::cout << "Quaternion to Euler Angles: " << std::endl << Q2E.transpose() << std::endl << std::endl;
}

//print
Quaternion to Euler Angles: 
-0.002792527  0.028448866 -1.324144561

4.1.3.2 欧拉角转四元数

间接法：

① 欧拉角? $\rightarrow$ ?旋转矩阵? $\rightarrow$ ?四元数

② 欧拉角? $\rightarrow$ ?旋转向量? $\rightarrow$ ?四元数

直接法：

看完前述?[文章倒数第二和第三章节]，不难得到绕各坐标轴旋转时对应的单位四元数分别为：

$\textit{\textbf{q}}_{X}(\alpha) = \begin{bmatrix} cos\frac{\alpha }{2}, sin\frac{\alpha }{2}, 0, 0 \end{bmatrix}^{T} \\ \textit{\textbf{q}}_{Y}(\beta) = \begin{bmatrix} cos\frac{\beta }{2}, 0, sin\frac{\beta }{2}, 0 \end{bmatrix}^{T} \\ \textit{\textbf{q}}_{Z}(\gamma) = \begin{bmatrix} cos\frac{\gamma }{2}, 0, 0, sin\frac{\gamma }{2} \end{bmatrix}^{T}$

按照Z-X-Y旋转顺序、内旋，使用四元数乘法即可得到最终所需四元数：

$\textit{\textbf{q}}=\textit{\textbf{q}}_{Z}(\gamma) \textit{\textbf{q}}_{X}(\alpha) \textit{\textbf{q}}_{Y}(\beta) \\ =\begin{bmatrix} cos\frac{\gamma }{2}cos\frac{\alpha }{2}cos\frac{\beta }{2}-sin\frac{\gamma }{2}sin\frac{\alpha }{2}sin\frac{\beta }{2}, cos\frac{\gamma }{2}sin\frac{\alpha }{2}cos\frac{\beta }{2}-sin\frac{\gamma }{2}cos\frac{\alpha }{2}sin\frac{\beta }{2}, cos\frac{\gamma }{2}cos\frac{\alpha }{2}sin\frac{\beta }{2}+sin\frac{\gamma }{2}sin\frac{\alpha }{2}cos\frac{\beta }{2}, sin\frac{\gamma }{2}cos\frac{\alpha }{2}cos\frac{\beta }{2}+cos\frac{\gamma }{2}sin\frac{\alpha }{2}sin\frac{\beta }{2} \end{bmatrix}^{T}$

即该四元数的实部和虚报分别为：

$q_{w}=cos\frac{\gamma }{2}cos\frac{\alpha }{2}cos\frac{\beta }{2}-sin\frac{\gamma }{2}sin\frac{\alpha }{2}sin\frac{\beta }{2} \\ q_{x}=cos\frac{\gamma }{2}sin\frac{\alpha }{2}cos\frac{\beta }{2}-sin\frac{\gamma }{2}cos\frac{\alpha }{2}sin\frac{\beta }{2} \\ q_{y}=cos\frac{\gamma }{2}cos\frac{\alpha }{2}sin\frac{\beta }{2}+sin\frac{\gamma }{2}sin\frac{\alpha }{2}cos\frac{\beta }{2} \\ q_{z}=sin\frac{\gamma }{2}cos\frac{\alpha }{2}cos\frac{\beta }{2}+cos\frac{\gamma }{2}sin\frac{\alpha }{2}sin\frac{\beta }{2}$

//code
{
    const double c_alpha_div2 = std::cos(0.5*alpha), c_beta_div2 = std::cos(0.5*beta), c_gamma_div2 = std::cos(0.5*gamma);
    const double s_alpha_div2 = std::sin(0.5*alpha), s_beta_div2 = std::sin(0.5*beta), s_gamma_div2 = std::sin(0.5*gamma);
    const auto E2Q_qw = c_gamma_div2*c_alpha_div2*c_beta_div2 - s_gamma_div2*s_alpha_div2*s_beta_div2;
    const auto E2Q_qx = c_gamma_div2*s_alpha_div2*c_beta_div2 - s_gamma_div2*c_alpha_div2*s_beta_div2;
    const auto E2Q_qy = c_gamma_div2*c_alpha_div2*s_beta_div2 + s_gamma_div2*s_alpha_div2*c_beta_div2;
    const auto E2Q_qz = s_gamma_div2*c_alpha_div2*c_beta_div2 + c_gamma_div2*s_alpha_div2*s_beta_div2;
    std::cout << "Euler Angles to Quaternion: " << Eigen::Vector4d(E2Q_qw, E2Q_qx, E2Q_qy, E2Q_qz).norm() << std::endl << E2Q_qx << "  "  << E2Q_qy << "  "  << E2Q_qz << "  "  << E2Q_qw << std::endl << std::endl;
}

//print
Euler Angles to Quaternion: 1.000000000
-0.012076975  0.007643055  0.788627217  0.614705493

4.2 四元数的缺点

①不够直观，运算稍显复杂。

②表达式虽炒鸡简单，但推导复杂。

五、Eigen完整应用程序

/*
 ************************************************************
 * @author    SLF
 * @date      27-Dec-2023
 ************************************************************
 */

#include <iostream>
#include <iomanip>
#include <vector>
#include <cmath>

// #include "Eigen/Core"
// #include "Eigen/Geometry"
// #include "Eigen/Eigenvalues"
#include "eigen3/Eigen/Core"
#include "eigen3/Eigen/Geometry"
#include "eigen3/Eigen/Eigenvalues"

// #include "Eigen/Eigen"
// #include "eigen3/Eigen/Eigen"

// #define USE_EIGEN_IMPL
#undef USE_EIGEN_IMPL

using namespace std;

int main(void) {
    //point
    const Eigen::Vector3d a(1.0, 2.0, 3.0);

    /*****************************
     ****** Rotation Matrix ******
     *****************************/
    Eigen::Matrix3d R;
    R << -0.243982607, -0.969731574, -0.009652007,
          0.969362354, -0.244157481,  0.026902609,
         -0.028444919, -0.002792523,  0.999591461;
    std::cout << "------------------" << std::endl;
    std::cout << std::setprecision(9) << std::fixed;
    std::cout << "Rotation Matrix: " << R.determinant() << std::endl << R << std::endl << std::endl;
    std::cout << "(1.0, 2.0, 3.0) after rotation (by matrix): " << std::endl << (R*a).transpose() << std::endl << std::endl;

    #ifdef USE_EIGEN_IMPL
    Eigen::Isometry3d T = Eigen::Isometry3d::Identity();
    // T.rotate(R);
    T.prerotate(R);
    T.pretranslate(Eigen::Vector3d(11, 22, 33));
    std::cout << "Transform Matrix: " << std::endl << T.matrix() << std::endl << std::endl;
    #else
    Eigen::Matrix4d T = Eigen::Matrix4d::Identity();
    T.block<3, 3>(0, 0) = R;
    T.block<3, 1>(0, 3) = Eigen::Vector3d(11, 22, 33);
    std::cout << "Transform Matrix: " << std::endl << T << std::endl << std::endl;
    #endif


    /*****************************
     ******   Axis-Angle    ******
     *****************************/
    const double angle = 1.817567592; //rad
    const Eigen::Vector3d axis(-0.015311407, 0.009690003, 0.999835819); //is unit vector
    const Eigen::AngleAxisd V(angle, axis);
    std::cout << "------------------" << std::endl;
    std::cout << "Axis-Angle: " << axis.norm() << std::endl << "angle=" << V.angle() << ", axis=" << V.axis().transpose() << std::endl << std::endl;
    std::cout << "(1.0, 2.0, 3.0) after rotation (by angle): " << std::endl << (V*a).transpose() << std::endl << std::endl;
    // std::cout << "(1.0, 2.0, 3.0) after rotation (by angle):" << std::endl << (Eigen::AngleAxisd(std::atan(1.0/2.0), Eigen::Vector3d::UnitZ())*a).transpose() << std::endl << std::endl; //rotate around the Z-axis


    /*** Axis-Angle to Rotation Matrix ***/
    const auto V2R = V.toRotationMatrix(); //V.matrix() == V.toRotationMatrix()
    std::cout << "------------------" << std::endl;
    std::cout << "Axis-Angle to Rotation Matrix: " << V2R.determinant() << std::endl << V2R << std::endl << std::endl;


    /*** Rotation Matrix to Axis-Angle ***/
    std::cout << "------------------" << std::endl;
    #ifdef USE_EIGEN_IMPL
    // const Eigen::AngleAxisd R2V(R);
    Eigen::AngleAxisd R2V;
    // R2V = R; //overloaded operator
    R2V.fromRotationMatrix(R);
    std::cout << "Rotation Matrix to Axis-Angle: " << R2V.axis().norm() << std::endl << "angle=" << R2V.angle() << ", axis=" << R2V.axis().transpose() << std::endl << std::endl;
    #else
    const double R2V_angle = std::acos(0.5*(R.trace()-1));
    const Eigen::EigenSolver<Eigen::MatrixXd> es(R);
    // std::cout << "eigenvalues: " << std::endl << es.eigenvalues().real().transpose() << std::endl;
    // std::cout << "eigenvectors: " << std::endl << es.eigenvectors().real() << std::endl;
    const auto eigenvalues = es.eigenvalues().real();
    int idx = 0;
    for (const auto val : eigenvalues) {
        if (1.0e-6 > std::fabs(val - 1.0)) {
            break;
        }
        idx++;
    }
    if (eigenvalues.rows() > idx) {
        const auto R2V_axis = es.eigenvectors().real().block<3, 1>(0, idx);
        std::cout << "Rotation Matrix to Axis-Angle: " << R2V_axis.norm() << std::endl << "angle=" << R2V_angle << ", axis=" << R2V_axis.transpose() << std::endl << std::endl;
    }
    #endif


    /*****************************
     ******  Euler Angles   ******
     *****************************/
    const double alpha = -0.002792527, beta = 0.028448867, gamma = 1.817448093;
    Eigen::Vector3d E(alpha, beta, gamma); //rad
    std::cout << "------------------" << std::endl;
    std::cout << "Euler Angles: (x,y,z)→(α,β,γ), intrinsic sequence z-x-y" << std::endl << E.transpose() << std::endl << std::endl;


    /*** Euler Angles to Rotation Matrix ***/
    Eigen::Matrix3d E2R;
    #if 1
    const double c_gamma = std::cos(gamma), c_alpha = std::cos(alpha), c_beta = std::cos(beta);
    const double s_gamma = std::sin(gamma), s_alpha = std::sin(alpha), s_beta = std::sin(beta);
    Eigen::Matrix3d R_x, R_y, R_z;
    R_x << 1.0, 0.0, 0.0,
           0.0, c_alpha, -s_alpha,
           0.0, s_alpha, c_alpha;
    R_y << c_beta, 0.0, s_beta,
           0.0, 1.0, 0.0,
           -s_beta, 0.0, c_beta;
    R_z << c_gamma, -s_gamma, 0.0,
           s_gamma, c_gamma, 0.0,
           0.0, 0.0, 1.0;
    E2R = R_z*R_x*R_y;
    #else
    #ifndef VAR_DEFINE_CONFLICT
    #define VAR_DEFINE_CONFLICT
    const double c1 = std::cos(gamma), c2 = std::cos(alpha), c3 = std::cos(beta);
    const double s1 = std::sin(gamma), s2 = std::sin(alpha), s3 = std::sin(beta);
    #endif
    E2R <<  c1*c3-s1*s2*s3, -c2*s1, c1*s3+c3*s1*s2,
            c3*s1+c1*s2*s3,  c1*c2, s1*s3-c1*c3*s2,
           -c2*s3,           s2,    c2*c3;
    #endif
    std::cout << "------------------" << std::endl;
    std::cout << "Euler Angles to Rotation Matrix: " << E2R.determinant() << std::endl << E2R << std::endl << std::endl;


    /*** Rotation Matrix to Euler Angles ***/
    #ifdef USE_EIGEN_IMPL
    const Eigen::Vector3d R2E_zxy = E2R.eulerAngles(2, 0, 1); //Note: The first parameter corresponds to the angle range of [0:pi], and the other two are [-pi:pi].
    const Eigen::Vector3d R2E(R2E_zxy(1), R2E_zxy(2), R2E_zxy(0));
    #else
    #ifndef VAR_DEFINE_CONFLICT
    #define VAR_DEFINE_CONFLICT
    const double c1 = std::cos(gamma), c2 = std::cos(alpha), c3 = std::cos(beta);
    const double s1 = std::sin(gamma), s2 = std::sin(alpha), s3 = std::sin(beta);
    #endif
    const auto R2E_z_angle = std::atan((c2*s1)/(c1*c2)); //why is supplementary angle ???
    const auto R2E_x_angle = std::asin(s2);
    const auto R2E_y_angle = std::atan((c2*s3)/(c2*c3));
    const Eigen::Vector3d R2E(R2E_x_angle, R2E_y_angle, R2E_z_angle);
    #endif
    std::cout << "------------------" << std::endl;
    std::cout << "Rotation Matrix to Euler Angles: " << std::endl << R2E.transpose() << std::endl << std::endl;


    /*** Euler Angles to Axis-Angle ***/
    Eigen::AngleAxisd E2V(Eigen::AngleAxisd(gamma, Eigen::Vector3d::UnitZ()) *
                          Eigen::AngleAxisd(alpha, Eigen::Vector3d::UnitX()) *
                          Eigen::AngleAxisd(beta, Eigen::Vector3d::UnitY())); 
    std::cout << "------------------" << std::endl;
    std::cout << "Euler Angles to Axis-Angle: " << E2V.axis().norm() << std::endl << "angle=" << E2V.angle() << ", axis=" << E2V.axis().transpose() << std::endl << std::endl;


    /*** Axis-Angle to Euler Angles ***/
    #ifdef USE_EIGEN_IMPL
    const auto V2E_zxy = V2R.eulerAngles(2, 0, 1);
    const Eigen::Vector3d V2E(V2E_zxy(1), V2E_zxy(2), V2E_zxy(0));
    #else
    const auto c_theta = std::cos(angle), s_theta = std::sin(angle);
    const auto V2E_z_angle = std::atan((axis(2)*s_theta-axis(0)*axis(1)*(1-c_theta))/(c_theta+std::pow(axis(1),2)*(1-c_theta))); //why is supplementary angle ???
    const auto V2E_x_angle = std::asin(axis(0)*s_theta+axis(1)*axis(2)*(1-c_theta));
    const auto V2E_y_angle = std::atan((axis(1)*s_theta-axis(0)*axis(2)*(1-c_theta))/(c_theta+std::pow(axis(2),2)*(1-c_theta)));
    const Eigen::Vector3d V2E(V2E_x_angle, V2E_y_angle, V2E_z_angle);
    #endif
    std::cout << "------------------" << std::endl;
    std::cout << "Axis-Angle to Euler Angles: " << std::endl << V2E.transpose() << std::endl << std::endl;


    /*****************************
     ******   Quaternion    ******
     *****************************/
    const double qw = 0.614705493, qx = -0.012076975, qy = 0.007643055, qz = 0.788627217;
    // const Eigen::Quaterniond(Eigen::Vector4d(qx,qy,qz,qw));
    const Eigen::Quaterniond Q(qw, qx, qy, qz);
    std::cout << "------------------" << std::endl;
    std::cout << "Quaternion: " << Q.squaredNorm() << std::endl << Q.coeffs().transpose() << std::endl << std::endl;
    std::cout << Q.x() << "  " << Q.y() << "  " << Q.z() << "  " << Q.w() << std::endl << std::endl;
    std::cout << "(1.0, 2.0, 3.0) after rotation (by quaternion): " << std::endl << (Q*a).transpose() << std::endl << std::endl; //overloaded operator
    std::cout << "(1.0, 2.0, 3.0) after rotation (by quaternion): " << std::endl << (Q*Eigen::Quaterniond(0,a(0),a(1),a(2))*Q.inverse()).coeffs().transpose() << std::endl << std::endl;
    

    /*** Quaternion to Rotation Matrix ***/
    const auto Q2R = Q.toRotationMatrix(); //Q.matrix() == Q.toRotationMatrix()
    std::cout << "------------------" << std::endl;
    std::cout << "Quaternion to Rotation Matrix: " << Q2R.determinant() << std::endl << Q2R << std::endl << std::endl;


    /*** Rotation Matrix to Quaternion ***/
    #ifdef USE_EIGEN_IMPL
    // const Eigen::Quaterniond R2Q(R);
    Eigen::Quaterniond R2Q;
    R2Q = R; //overloaded operator
    #else
    const double R2Q_qw = 0.5*std::sqrt(1.0+R(0,0)+R(1,1)+R(2,2));
    const double R2Q_qx = (R(2,1)-R(1,2))/(4*R2Q_qw);
    const double R2Q_qy = (R(0,2)-R(2,0))/(4*R2Q_qw);
    const double R2Q_qz = (R(1,0)-R(0,1))/(4*R2Q_qw);
    const Eigen::Quaterniond R2Q(R2Q_qw, R2Q_qx, R2Q_qy, R2Q_qz);
    #endif
    std::cout << "------------------" << std::endl;
    std::cout << "Rotation Matrix to Quaternion: " << R2Q.squaredNorm() << std::endl << R2Q.coeffs().transpose() << std::endl << std::endl;


    /*** Quaternion to Axis-Angle ***/
    #ifdef USE_EIGEN_IMPL
    // const Eigen::AngleAxisd Q2V(Q);
    Eigen::AngleAxisd Q2V;
    Q2V = Q; //overloaded operator
    #else
    const Eigen::AngleAxisd Q2V(2.0*std::acos(qw), Eigen::Vector3d(qx,qy,qz)/std::sqrt(1.0-std::pow(qw,2)));
    #endif
    std::cout << "------------------" << std::endl;
    std::cout << "Quaternion to Axis-Angle: " << Q2V.axis().norm() << std::endl << "angle=" << Q2V.angle() << ", axis="  << Q2V.axis().transpose() << std::endl << std::endl;


    /*** Axis-Angle to Quaternion ***/
    #ifdef USE_EIGEN_IMPL
    // const Eigen::Quaterniond V2Q(V);
    Eigen::Quaterniond V2Q;
    V2Q = V; //overloaded operator
    #else
    const auto qxyz = std::sin(0.5*angle) * axis;
    Eigen::Quaterniond V2Q(std::cos(0.5*angle), qxyz(0), qxyz(1), qxyz(2));
    #endif
    std::cout << "------------------" << std::endl;
    std::cout << "Axis-Angle to Quaternion: " << V2Q.squaredNorm() << std::endl << V2Q.coeffs().transpose() << std::endl << std::endl;


    /*** Quaternion to Euler Angles ***/
    #ifdef USE_EIGEN_IMPL
    const Eigen::Vector3d Q2E_zxy = Q.matrix().eulerAngles(2, 0, 1);
    const Eigen::Vector3d Q2E(Q2E_zxy(1), Q2E_zxy(2), Q2E_zxy(0));
    #else
    const auto qw2 = std::pow(qw,2);
    const auto qx2 = std::pow(qx,2);
    const auto qy2 = std::pow(qy,2);
    const auto qz2 = std::pow(qz,2);
    const auto Q2E_z_angle = std::atan((2.0*qw*qz-2.0*qx*qy)/(qw2-qx2+qy2-qz2)); //why is supplementary angle ???
    const auto Q2E_x_angle = std::asin(2.0*qy*qz+2.0*qw*qx);
    const auto Q2E_y_angle = std::atan((2.0*qw*qy-2.0*qx*qz)/(qw2-qx2-qy2+qz2));
    const Eigen::Vector3d Q2E(Q2E_x_angle, Q2E_y_angle, Q2E_z_angle);
    #endif
    std::cout << "------------------" << std::endl;
    std::cout << "Quaternion to Euler Angles: " << std::endl << Q2E.transpose() << std::endl << std::endl;


    /*** Euler Angles to Quaternion ***/
    const double c_alpha_div2 = std::cos(0.5*alpha), c_beta_div2 = std::cos(0.5*beta), c_gamma_div2 = std::cos(0.5*gamma);
    const double s_alpha_div2 = std::sin(0.5*alpha), s_beta_div2 = std::sin(0.5*beta), s_gamma_div2 = std::sin(0.5*gamma);
    const auto E2Q_qw = c_gamma_div2*c_alpha_div2*c_beta_div2 - s_gamma_div2*s_alpha_div2*s_beta_div2;
    const auto E2Q_qx = c_gamma_div2*s_alpha_div2*c_beta_div2 - s_gamma_div2*c_alpha_div2*s_beta_div2;
    const auto E2Q_qy = c_gamma_div2*c_alpha_div2*s_beta_div2 + s_gamma_div2*s_alpha_div2*c_beta_div2;
    const auto E2Q_qz = s_gamma_div2*c_alpha_div2*c_beta_div2 + c_gamma_div2*s_alpha_div2*s_beta_div2;
    std::cout << "------------------" << std::endl;
    std::cout << "Euler Angles to Quaternion: " << Eigen::Vector4d(E2Q_qw, E2Q_qx, E2Q_qy, E2Q_qz).norm() << std::endl << E2Q_qx << "  "  << E2Q_qy << "  "  << E2Q_qz << "  "  << E2Q_qw << std::endl << std::endl;

    return 0;
}

//build
g++ -W -g -o exe main.cpp

//run
./exe

六、总结回顾

由前所述，各种旋转变换之间都可相互转换（直接转换、间接转换）。但由于旋转向量和欧拉角存在奇异性（有奇点），导致旋转矩阵转旋转向量、旋转矩阵转欧拉角、四元数转旋转向量、四元数转欧拉角的变换关系式在某些情况不成立，所以应尽量避免使用。

下图描绘了四种旋转表示形式之间的转换关系，对于Eigen库可直接支持的转换及其方法进行了显式标注，对于Eigen库暂不支持的转换或方法，详见本文前面各章节介绍。

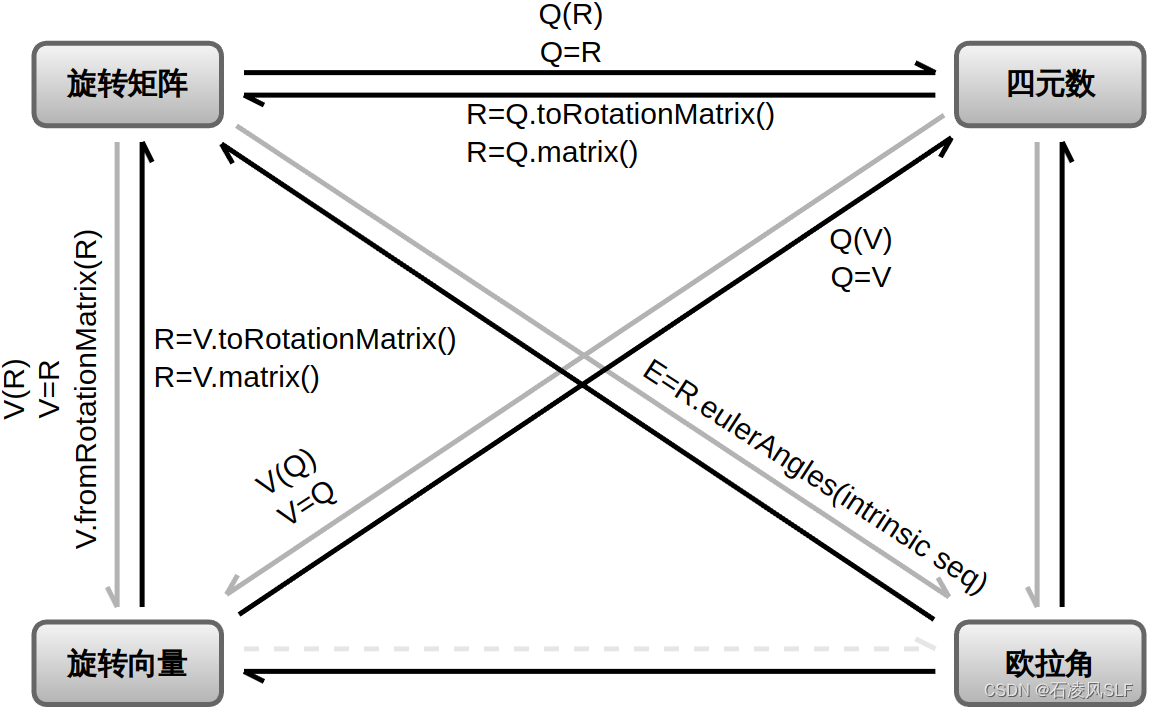
Eigen库中对此四种旋转表示形式都定义了相应的数据结构（双精度、单精度），分别如下：

旋转矩阵（3×3）：Eigen::Matrix3d、Eigen::Matrix3f

旋转向量（3×1）：Eigen::AngleAxisd、Eigen::AngleAxisf

欧拉角（3×1）：Eigen::Vector3d、Eigen::Vector3f

四元数（4×1）：Eigen::Quaterniond、Eigen::Quaternionf

显而易见，旋转向量和欧拉角最轻量（三个浮点数即可描述三维旋转），但均存在奇异性。并且欧拉角的存在仅是为了在描述旋转时方便主观理解，本身不具备计算特性，最终一般还是要转换为旋转矩阵，或者四元数来参与计算。

旋转矩阵明显最冗余不紧凑，综合对比来看，四元数是最佳选择（不存在奇异性，四个浮点数描述三维旋转）。

此外，转换的中间过程越少，精度损失越少。

References:

Maths - Rotation conversions - Martin Baker（YZX intrinsic sequence）

视觉SLAM十四讲：从理论到实践（第2版）

怎样通俗理解四元数 - 知乎

https://en.wikipedia.org/wiki/Euler_angles

https://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula

文中纰漏请在评论区交流反馈。

总结、编辑不易，转载请注明出处！！！

文章来源:https://blog.csdn.net/jiqiren_dasheng/article/details/134153828
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！