【解惑】全搞懂弗洛伊德算法

????????Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。弗洛伊德算法可以说是求最短距离算法中代码最简单的（就三层for循环），但是它的思想却不简单，本文的重点在于彻底搞懂弗洛伊德算法，解答可能的疑点！

1. 弗洛伊德算法的基本思想

????????弗洛伊德算法是求解多源点的最短路径，当不考虑源点到终点的中间节点，从源点直接到达终点，如 i -> j，最短路程就是节点之间的权值 weight[i][j]。

????????现在需要考虑从中间节点中转到终点的路程是否会比直接抵达终点更短，假设中转节点为 k=0，即要判断 weight[i][0]+weight[0][j] 是否比既有的 weight[i][j] 小，如果是则替换。针对每个源点到每个终点都需要考虑加入中转节点后最短距离是否需要更新。

????????我们记这样的一轮次更新为 D0[i][j]，D-1[i][j]=weight[i][j] ，如果考虑 k 为一般值，那么各源点到各终点的最短距离是在上一轮更新 Dk-1[i][j] 的基础上进一步更新得到的，即

Dk[i][j] = min{ Dk-1[i][j], Dk-1[i][k] + Dk-1[k][j] }

????????至此，我们已经能够大体了解弗洛伊德算法更新最短距离算法的核心其实是借助了动态规划的思想，问题的初态是节点之间的权值，每一轮次的更新都是在上次的基础上完成的，直到完成针对所有中转节点的更新，各源点到各终点的最短距离就最终确定。

2. 弗洛伊德算法代码思路

（1）三层 for 循环

? ? ? ? 对每个中间节点 k 都要从一而终地对各个源点到各个终点的最短路径进行更新，所以整个过程需要使用三层 for 循环，注意三层 for 循环的顺序不能交换，如采用了下面的做法，相当于针对一个源点到终点的问题就去找到一个最好的 k 更新最短距离，这个最短距离就确定了，在后面的更新中就不再变动，这显然不对。

for(int i=0; i<n; i++)
for(int j=0; j<n; j++)
for(int k=0; k<n; k++)

????????应该采用下面的方式：

for(int k=0; k<n; k++)
for(int i=0; i<n; i++)
for(int j=0; j<n; j++)

（2）前驱节点

????????用一个二维数组 dis 来记录各源点到各终点的最短距离并在算法运行过程中不断更新。如果要厘清最短路程的路径就需要定义一个 parent 数组来记录节点的前驱节点，同样地，针对不同源点节点的前驱节点可能是不同的，所以 parent 数组也需要用二维的数组，此外，parent 数组跟随 dis 数组更新即可。

总的来说，弗洛伊德算法的思想是巧妙的，但代码是简洁的：

示例代码：

// 核心：弗洛伊德算法（三层循环）
    public void floyd() {
        // 变量保持距离
        int len = 0;
        // 对中间顶点遍历， k 是中间顶点的下标 [A, B, C, D, E, F, G]
        for (int k = 0; k < dis.length; k++) {
            // 从i顶点开始出发 [A, B, C, D, E, F, G]
            for (int i = 0; i < dis.length; i++) {
                // 到达j顶点 // [A, B, C, D, E, F, G]
                for (int j = 0; j < dis.length; j++) {
                    // 求出从i 顶点出发，经过 k中间顶点，到达 j 顶点距离
                    len = dis[i][k] + dis[k][j];
                    if (len < dis[i][j]) {       // 若len小于 dis[i][j]
                        dis[i][j] = len;        // 更新距离
                        pre[i][j] = pre[k][j];  // 更新前驱顶点
                    }
                }
            }
        }
    }

3. 弗洛伊德算法的时间复杂度

O(n3)

4. 弗洛伊德算法的一些疑惑

（1）弗洛伊德算法是如何处理中转节点有多个的情况？

答：需要重新理解 dis 数组 Dk[i][j] = min{ Dk-1[i][j], Dk-1[i][k] + Dk-1[k][j] }。Dk-1[i][k]是源点 i 到终点 k 的最短距离，会考虑 i 途经其他节点再到达 k 的情况，这种情况可能在前面已经被更新并记录到 dis 数组了。

（2）会不会出现上面这种情况其实还没被记录，如第一个中转节点在更新时，很多信息都还是不完善的，这会有影响吗？

答：这个问题的确很有迷惑性。可以这样考虑，我们要关注的是源点 i 到终点 k 的最短距离的更新情况，而不应该局限于单个节点。前面的中转节点所做的更新因为信息还不完善，所得出的并不是最短的距离并不意外，因为这个最短距离并没有因为一个中转节点的遍历结束后就确定了，而且这些更新并不是没有意义，是作为后面的更新的基础。

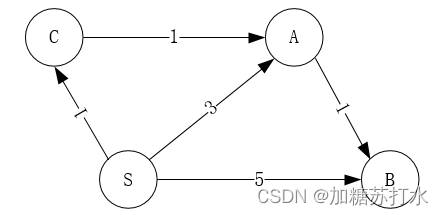
????????如下图，A作为首个中转节点在在更新源点 S 到终点 B 的最短距离时，在判断 dis[S][A] + dis[A][B] 与 dis[S][B] 的大小关系时，dis[S][B] = weight[S][B] = 2，dis[A][B] = weight[A][B] = 1，而 dis[S][A] 由于还未更新 S 到 A 的最短距离依旧取 weight[S][A] = 2，实际上我们知道 dis[S][A] 应取 dis[S][C] + dis[C][A] = 2，即最短的路径是 S -> C -> A -> B 的四个节点的路径，所以此轮的更新中得到的 S 到 B 的最短距离并不是最短的。但是我们要看到 A 作为中转节点更新了 dis[C][B] = dis[C][A] + dis[A][B] = 2，在以 C 为中转节点时，就自然地选择了四个点的路径，即 dis[S][B] = dis[S][C] + dis[S][C] = 1 + 2 =3，这时就能符合预期了。

5. 弗洛伊德算法与迪克斯特拉算法

????????在求源点到终点的最短距离时，Dijkstra算法是求单源最短路径的，Floyd算法是求多源最短路径的，若非要解决多源点问题，迪克斯特拉算法也是可行的：

• （1） Dijkstra算法每次是单源点，遍历完每个源点也可以实现所有点的最短距离的求解，时间复杂度为O(n3)；

• （2） Floyd（弗洛伊德算法）对标多源点的最短距离求解，算法复杂度为O(n3)。

????????对于稀疏的图，采用n次Dijkstra比较出色，对于稠密的图，推荐使用Floyd算法。此外，迪克斯特拉算法不能处理有负数权重的边。

specially: Bellman-ford 算法也可以处理负数边