03. BI - 详解机器学习神器 XGBoost

本文专辑 : 茶桁的AI秘籍 - BI篇
原文链接: https://mp.weixin.qq.com/s/kLEg_VcxAACy8dH35kK3zg
Hi,你好。我是茶桁。
学习总是一个循序渐进的过程,之前两节课的内容中,咱们去了解了LR和SVM在实际项目中是如何使用的,我给大家看了两个项目都是跟分类相关,一个是员工离职预测,一个是男女声音识别。
其实也能看到,男女声音识别也不一定都要用神经网络,能找到一些关键特征把它转化为结构化的数据你也可以用机器学习来完成预测,而且机器学习的效果还是非常好,基本上都有百分之97,98的准确性。
那今天这节课主要给大家讲解的是「机器学习的神器」,也是今天最主要的内容。
这个内容希望大家多去仔细阅读,如果你遇到哪些问题可以给我留言,文章下或者私信都可以,基本上,一些容易解答的问题我都会给予回复,大家保持一个良好的学习的方法。
集成学习
这些机器学习的神器都跟集成学习相关,先给大家看一个概念叫集成学习。集成学习就是把多个分类器合到一起,可以把它理解成叫三个臭裨将顶个诸葛亮。

集中学习里面有些策略,Bagging是一种,它像一个袋子一样,数据是放到袋子里面去,叫有放回的抽样方式。这个袋子里面如果你要做一个分类的模型会按照少数服从多数。最简单的就是一个陪审团,看一看大家投票的情况,这是分类问题。回归问题我们要用的是大家的平均值,你预测一下薪酬,他预测一下薪酬,把大家预测结果相加以后除上个数就是求平均值。这些都是一个banging的策略,集中学习把这些大家的结果给合并到一起。
Stacking叫做堆,什么叫Stacking?上图中下面的部分就是Stacking,我们把它分成两类分类器,分类器1,也就是前面的Classifier做了特征的提取,分类器2,Meta Classifier做了分类的过程。它是属于先后两阶段,先做第一种再做第二种,这是有先后逻辑顺序关系。如果是Bagging是没有先后逻辑关系。它是一个并行方法。你做你的,我做我的,最后我们可以综合起来,这个结果没有先后逻辑关系。而Stacking的话是有一个先后逻辑关系的,这是集成学习的不同种的学习的方式。
还有一种学习方式的话叫Boosting,Boosting中文可以把它称为叫提升,它也有先后的顺序。

我们看这张图,原始的数据给了模型,第一个分类器模型做了以后得到一些新的一些数据,再喂给第二个模型,然后再生成一些数据再喂给第三个模型,这三个模型之间是有顺序的。先计算第一个,再计算后面的第二个,再计算第三个,所以这种Boosting的方法是有一些顺序的关系。
通过Boosting的方式可以把弱分类器结合到一起形成一个强的分类器,这是它的一个Boosting的关系。Boosting有两个比较重要的算法,一个AdaBoost(自适应提升), 一个是Gradient Boosting(梯度提升)。这两种方法在咱们之前的机器学习课程中都有详细的讲解。
AdaBoost是使用前面的学习器用简单的模型去适配数据,然后分析错误。然后会给予错误预测的数据更高权重,然后用后面的学习器去修复。
所以集成学习是有三种模式,Bagging是一种,Stacking是一种,还有就是Boosting。总的来说都是把多个分类器组合起来,会胜过一个分类器。这几中模型之间比较常见的模型是Boosting和Bagging。

我们对这两个做个对比。
- 在结构上,Bagging是基分类器并行处理,而Boosting是串行处理。
- 训练集上,Bagging的基分类器训练是独立的,而Boosting的训练集是依赖于之前的模型
- 在作用上,Bagging的作用是减少variance, 而Boosting在于减少bias。
并行的方式和串形的方法没有什么特别的好坏之分,如果要去判断也是跟数据相关。我今天讲解的神器是属于最后一种,就是Boosting的方式,所以它应该是一个串形的方法。
这种分类器里面有很多种,上面我介绍了两个算法,一个是AdaBoost,一个是Gradient Boosting,那我们主要看看后面这种算法。这个算法中包含了几个比较重要的工具,有XGBoost、LightGBM、CatBoost以及NGBoost,实际上是对GBDT方法的不同实现,针对同一目标做了不同的优化处理。基本上出现的年限如下:
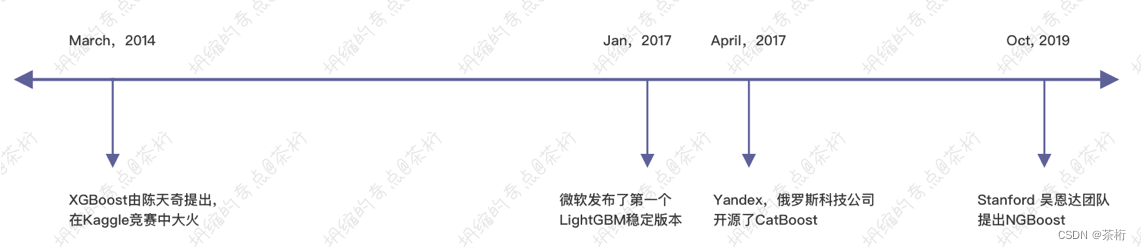
Boosting这种方式典型代表是XGBoost、LightGBM和CatBoost,NGBoost采用的boosting的方法跟前三种boosting不太一样,通常我们机器学习的神器还是指的前面三种。当然,近些年还有一些新的工具,比如H2O GBM,以及TensorFlow Boosted Trees(TFBT),咱们我们不去探讨它们,以后有机会写进阶课程的时候再说。
XGBoost最早提出来的是2014年,它是由陈天奇提出来的,提出来以后在Kaggle的比赛中是大火,基本上在2014年那个阶段只要你参加机器学习的比赛必用XGBoost,而且第一名基本上都是XGBoost,效果是最好的。
三年之后在2017年,微软提出来了一个lightGBM的版本,它是站在原来的XGBoost基础上做了一些简化,让它的版本更轻,轻的一个优势就是快。所以LightGBM占用内存更少,速度更快。
三个月之后俄罗斯的一家公司叫Yandex又做了一个新的版本,叫CatBoost,这家公司你可以把它理解成是俄罗斯的Google,是个科技巨头,也做测速引擎,同时也开源很多的机器学习的工具箱,那我们现在用的CatBoost就是Yandex提出来的一个模型。
XGBoost
https://arxiv.org/abs/1603.02754

XGBoost是2014年提出来的模型,它本身是基于树的。一般来说用的是CART回归树。这个是一个决策树,这是它的机器学习的模型。
我们现在要去完成一个预测y值,一个人是否喜欢电子游戏。就是电子游戏的市场跟哪些特征相关,年龄、性别、职业这些特征。前面是我们的X,有很多X,最后是那个y。
现在如果要建一棵树,用一棵角色树可能会建出来如图的一个过程。先判断他的age是不是小于15岁,如果小于15岁就走左边,再判断他的性别是不是男性,如果是男性我们就认为他会玩两个小时,如果不是男性就是0.1个小时。如果他是大于15岁我们就认为他是-1。
这个是其中一棵树的一个结果,他的预测是在叶子节点里面会有一个数值,这等于他的输出,所以输出都是在叶子节点里,中间那颗分支都是按照不同的逻辑来做个判断。
XGBoost它本身是集中学习,其实它背后的那个过程原理叫GBDT,大家先知道就好了,我们今天没有详细展开GBDT,这个是属于它的理论。就是说我有多少棵树一起来学习。就是之前看到那张图上的模型,依照数据流,Model1先去做,做完以后Model2去做,再做完以后Model3去做。它本身的原理就是多棵树相加。
那GBDT的理论版本是这样,XGBoost是它的工程版本。工程版本的目的是要更加的泛化,所以它主要是在原来GBDT的基础上又加了一个叫做正则化项:
目标函数 = 损失函数 + 正则化项 O b j ( Θ ) = L ( Θ ) + Ω ( Θ ) \begin{align*} 目标函数 = 损失函数 + 正则化项 \\ Obj(\varTheta) = L(\varTheta) + \Omega(\varTheta) \end{align*} 目标函数=损失函数+正则化项Obj(Θ)=L(Θ)+Ω(Θ)?
这里, L ( Θ ) L(\varTheta) L(Θ)是损失函数,拟合数据。 Ω ( Θ ) \Omega(\varTheta) Ω(Θ)是正则化项,惩罚复杂模型。
我们的目标函数是由损失函数加正则化项。一般我们要判断的是想让它的预测结果和实际值更小,这个叫loss functio,之前课程中,我们一直跟loss打交道。多出来的结果叫y’, 和实际值的y之间, 我们会计算一个损失函数。
比如说我们要用用MSE做回归值,(y’ - y)^2,这等于它loss function。
所以,正则化项意义就是对我们的叶子节点做了一惩罚项。
Ω ( f t ) = γ T + 1 2 λ ∑ j = 1 T w j 2 \begin{align*} \Omega(f_t) = \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2 \end{align*} Ω(ft?)=γT+21?λj=1∑T?wj2??
整个 Ω ( f t ) \Omega (f_t) Ω(ft?)用于控制树的复杂度,防止过拟合,使得模型更简化,也使得最终的模型的预测结果更稳定。
这个复杂的公式里, T代表的就是叶子数量,你想,如果你的决策数叶子数量很多,这个数模型就会很复杂。
w_j 是叶子分数的L2正则项, 如果它的叶子的分数也是很大的话,也比较复杂,所以我们希望这棵树简单一点,没有这么多的叶子节点,而且叶子节点的数值也比较小一点。这样就是一个稍微小巧一点的模型。
γ \gamma γ是加入新叶子节点引入的复杂度代价。
那为什么要加正则化项呢?我给大家举个场景,你自己体会一下。我们的目标是希望损失函数最小化,比如说我们目标是想要挣更多的钱,有两种人a和b。a月薪是2万块钱,他每天就是朝九晚五,办公室的白领。b是网约车司机,每天早上6点出门,晚上12点回家,他也是月薪2万块钱。
你想办公室的白领他的模型相对来说比较简单一点,后面我们的系数就是大家不需要太多去努力,大概读出来结果-1,-0.1,+1, +0.1就好了。
网约车司机他会非常的奔波,很累。可能这个系数抖动比较大,最后得出结果+10, +20, -10, -20等等。
现在想一想,同样月薪2万块钱,你们希望是做a还是做b呢?我们同样可以得到这样一个结果,是希望是像办公室白领一样轻轻松松可以达到你的loss function这样的一个目标,还是希望像网约车司机一样特别的辛苦,很复杂。早上6点出门,晚上是24点回家。那大部分人应该都是a,这逻辑是一样的。
我们希望我们的那棵树没有那么的复杂,也能达到比较好的效果。所以在我们的目标函数过程中统计了两个代价,一个代价叫做loss function,损失代价,还有一个就是模型的代价。模型代价跟谁相关呢?跟模型的叶子数和叶子的分数相关。

以上就把目标函数的两个过程,损失函数和正则化项给大家讲完了。
接下来我们就详细的看一看它是怎么去做的。
预测函数,样本的预测结果=每棵树预测分数之和。
y ^ i = ∑ k = 1 k f k ( x i ) \begin{align*} \hat y_i = \sum^k_{k=1}f_k(x_i) \end{align*} y^?i?=k=1∑k?fk?(xi?)?
我们对目标函数进行优化
O b j ( Θ ) = ∑ i l ( y i , y ^ i ) + ∑ k Ω ( f k ) Ω ( f ) = γ T + 1 2 λ ∣ ∣ w ∣ ∣ 2 \begin{align*} Obj(\varTheta) & = \sum_il(y_i, \hat y_i)+\sum_k\Omega(f_k) \\ \Omega(f) & = \gamma T + \frac{1}{2}\lambda ||w||^2 \end{align*} Obj(Θ)Ω(f)?=i∑?l(yi?,y^?i?)+k∑?Ω(fk?)=γT+21?λ∣∣w∣∣2?
我们在原来的loss function里面加了一个正则化项,下面的那个是正则化项的公式,前面是叶子节点的数量,后面是叶子节点的分数。我们希望目标函数最小化,把这个目标函数写成以下的一个过程:
O b j t = ∑ i = 1 n l ( y i , y ^ i t ? 1 + f t ( x i ) ) + Ω ( f t ) + c o n s t a n t \begin{align*} Obj^t = \sum_{i=1}^n l(y_i, \hat y_i^{t-1} + f_t(x_i))+\Omega(f_t) + constant \end{align*} Objt=i=1∑n?l(yi?,y^?it?1?+ft?(xi?))+Ω(ft?)+constant?
集成学习的树是由多棵树来完成的,如果你现在做的是t棵树,前面那个结果就是t-1棵树。t-1棵树的结果加上 Δ \varDelta Δ,也就是 f t ( x i ) f_t(x_i) ft?(xi?),就说第t棵树的结果。之前咱们说的model1, model2, model3这是三棵树, 如果t等于3的话前面两棵树是t-1,预测结果加上第三棵树的预测结果。
这两个过程我们都是拿它做一个loss function的一个组合,再加上正则化项,再加上一个常数项,这等它的目标函数。
对这个函数改进,进行二阶泰勒展开:
f ( x + Δ x ) ≈ f ( x ) + f ′ ( x ) Δ x + 1 2 f ′ ′ ( x ) Δ x 2 \begin{align*} f(x+\varDelta x) \approx f(x) + f'(x)\varDelta x + \frac{1}{2} f''(x)\varDelta x^2 \end{align*} f(x+Δx)≈f(x)+f′(x)Δx+21?f′′(x)Δx2?
那关于泰勒展开,我在数学基础篇里有一篇专门来讲这个。现在我们只要知道它是一个定理,这个定理就是说你的变量 x + Δ x x+\varDelta x x+Δx可以近似的把它展开出来这样。
y ^ i ( 0 ) = 0 y ^ i ( 1 ) = f 1 ( x i ) = y ^ ( 0 ) + f 1 ( x i ) y ^ i ( 2 ) = f 1 ( x i ) + f 2 ( x i ) = y ^ ( 1 ) + f 2 ( x i ) ? y ^ i ( t ) = ∑ k = 1 t f k ( x i ) = y ^ i ( t ? 1 ) + f t ( x i ) \begin{align*} \hat y_i^{(0)} & = 0 \\ \hat y_i^{(1)} & = f_1(x_i) = \hat y^{(0)} + f_1(x_i) \\ \hat y_i^{(2)} & = f_1(x_i) + f_2(x_i) = \hat y^{(1)} + f_2(x_i) \\ \cdots & \\ \hat y_i^{(t)} & = \sum_{k=1}^tf_k(x_i) = \hat y_i^{(t-1)} + f_t(x_i) \end{align*} y^?i(0)?y^?i(1)?y^?i(2)??y^?i(t)??=0=f1?(xi?)=y^?(0)+f1?(xi?)=f1?(xi?)+f2?(xi?)=y^?(1)+f2?(xi?)=k=1∑t?fk?(xi?)=y^?i(t?1)?+ft?(xi?)?
那这个式子就可以这样推理得到。其中 y ^ i ( t ) \hat y_i^{(t)} y^?i(t)?是第t轮的模型预测, y ^ i ( t ? 1 ) \hat y_i^{(t-1)} y^?i(t?1)?是保留前t-1轮的模型预测, 而 f t ( x i ) f_t(x_i) ft?(xi?)是加入新的预测函数。
我们可以做多阶泰勒展开,二阶泰勒展开呢相对简单一点。现在只要知道有这么一个概念,这个概念是做一个近似的过程即可。今天就不去讲这个数学的推导了,关于如何利用数学进行推导,大家回到我数学篇里专门有一篇讲泰勒展开的一节去好好补一下基础。
那这个过程就还是一个loss function,这里就是一个任何的function都是一样的。后面这个f’(x)是一个导数,f’是一阶导数,f’'是二阶导数,就是做完一阶以后再去做一阶。
一阶导数乘上 Δ x \varDelta x Δx,再加上二阶导数乘上 Δ x 2 \varDelta x^2 Δx2,这等于二阶泰勒展开,这是一个定理。那这个定理代入的就是刚才这套过程。
我们来看定义:
$$
\begin{align*}
g_i & = \partial_{\hat y^{(t-1)}}l(y_i, \hat y^{(t-1)}) \
h_i & = \partial^2_{\hat y^{(t-1)}}l(y_i, \hat y^{(t-1)}) \
Obj^t & \approx \sum_{i=1}^n \left [ l(y_i, \hat y^{(t-1)}) + g_if_t(x_i) + \frac{1}{2}h_if_t^2(x_i) \right ] + \Omega(f_t) + constant
\end{align*}
$$
这里,f(x)就是等于 l ( y i , y ^ i ( t ? 1 ) ) l(y_i, \hat y_i^{(t-1)}) l(yi?,y^?i(t?1)?),后面这个 f t ( x i ) f_t(x_i) ft?(xi?)不就是 Δ x \varDelta x Δx吗,然后f’(x)是定义成了一阶导数,用g来代表,再之后是 Δ x 2 \varDelta x^2 Δx2,它就是 f t 2 ( x i ) f_t^2(x_i) ft2?(xi?)。那个二阶导数用h来代表,前面再把1/2拿过来。
这样目标函数我们就把它做了个改写,我们把它用二阶泰勒展开做了个改写,中间的一阶导数项用g,二阶导数项用h,所以它是个约等于。
有了这个流程以后,刚才这是个约等于,是用二阶泰勒展开。还可以再去详细的去看一看, f_t(x_i),这是第7棵树的结果,因为咱们用的是个决策树,它的结果是在叶子节点,那么叶子节点可以作为定义。它叶子节点假设是w,那它的叶子节点的平方也是w的平方,我们再加上后面的正则化项,正则化项是刚刚我们定义好的 γ T + λ 1 2 ∑ i = 1 T w j 2 \gamma T+\lambda\frac{1}{2}\sum_{i=1}^T w_j^2 γT+λ21?∑i=1T?wj2?, 这是陈天奇定义好的一个公式。这样一个推导我们还可以再把它去做一个合并的过程,这个过程就不完全展开了,可以自己看一下,我们来看一个完整的推导:
O b j t = ∑ i = 1 n [ g i f t ( x i ) ? 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) = ∑ i = 1 n [ g i w q ( x i ) + 1 2 h i w q ( x i ) 2 ] + γ T + λ 1 2 ∑ i = 1 T w j 2 = ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T \begin{align*} Obj^t & = \sum_{i=1}^n \left [ g_if_t(x_i) - \frac{1}{2}h_if_t^2(x_i) \right ] + \Omega(f_t) \\ & = \sum_{i=1}^n \left [ g_iw_{q(x_i)} + \frac{1}{2} h_iw^2_{q(x_i)} \right ] + \gamma T + \lambda\frac{1}{2}\sum_{i=1}^T w_j^2 \\ & = \sum_{j=1}^T \left [\left( \sum_{i\in I_j} g_i \right) w_j + \frac{1}{2} \left ( \sum_{i\in I_j} h_i + \lambda \right ) w_j^2 \right] + \gamma T \end{align*} Objt?=i=1∑n?[gi?ft?(xi?)?21?hi?ft2?(xi?)]+Ω(ft?)=i=1∑n?[gi?wq(xi?)?+21?hi?wq(xi?)2?]+γT+λ21?i=1∑T?wj2?=j=1∑T? ? ?i∈Ij?∑?gi? ?wj?+21? ?i∈Ij?∑?hi?+λ ?wj2? ?+γT?
T为叶子节点数量, I j I_j Ij?定义为每个叶子节点里面的样本集合 I j = { i ∣ q ( x i ) = j } I_j = \{ i | q(x_i) = j \} Ij?={i∣q(xi?)=j}, f t ( x i ) = w q ( x i ) f_t(x_i) = w_{q(x_i)} ft?(xi?)=wq(xi?)?即每个样本所在叶子节点索引的分数(叶子权重w)。
那么我们就可以看到,g是做了一个求和项,h也做了一个求和项。
所以我们就把一阶导数的求和用一个大G去表达,
G
j
=
∑
i
∈
I
j
g
i
G_j = \sum_{i\in I_j} g_i
Gj?=∑i∈Ij??gi?,二阶的求和用个大H来做表达
H
j
=
∑
i
∈
I
j
h
i
H_j = \sum_{i\in I_j} h_i
Hj?=∑i∈Ij??hi?,就是把这个过程用大G和大H来去做一个表达,那我们上面最后那一步的那个复杂公式就可以写成:
O b j t = ∑ j = 1 T [ G j w j + 1 2 ( H j + λ ) w j 2 ] + γ T \begin{align*} Obj^t = \sum_{j=1}^T \left[ G_jw_j + \frac{1}{2}(H_j + \lambda) w_j^2 \right] + \gamma T \end{align*} Objt=j=1∑T?[Gj?wj?+21?(Hj?+λ)wj2?]+γT?
以上就把它的目标函数做了一个改写, 那现在我们是希望这个目标函数是越大越好,还是越小越好?自然是希望它越小越好。那什么时候得到最小值?导数为0的时候,就是对 ? O b j ? w j \frac{\partial Obj}{\partial w_j} ?wj??Obj?求偏导,,那求偏导就得到:
? O b j ? w j = G j + ( H j + λ ) w j = 0 \begin{align*} \frac{\partial Obj}{\partial w_j} = G_j + (H_j + \lambda)w_j = 0 \end{align*} ?wj??Obj?=Gj?+(Hj?+λ)wj?=0?
导数等于0的时候,我们就可以求到极值,它等于0的时候我们可以求解得:
w j = ? G j H j + λ O b j = ? 1 2 ∑ j = 1 T G j 2 H j + λ + γ T \begin{align*} w_j & = - \frac{G_j}{H_j + \lambda} \\ Obj & = -\frac{1}{2} \sum_{j=1}^T \frac{G_j^2}{H_j + \lambda} + \gamma T \end{align*} wj?Obj?=?Hj?+λGj??=?21?j=1∑T?Hj?+λGj2??+γT?
先求得 w j w_j wj?之后再将它代入到前面那个公式,我们就可以得到Obj。
所以要想让目标函数最小,我们可以直接求出来w_j的极值以及最小化的那个Obj。
有了这个过程之后我们一起看一看,我们的XGBoost是怎么去进行运算的。
我们的Obj的目标函数也是称为一个叫结构分数(打分函数),我们希望这个结构分数越小越好。越小就代表它这个结构越稳定。

我们看图,第一个部分,判断is male为yes的时候的叶子是一个样本,为no的时候是一个样本,那判断age < 15为no的时候是三个样本。如果三个样本输出的结果的话,我们的的大G就是三个样本的之和,大H也是这三个样本的h,二阶导数之和。
Obj是衡量模型好坏的标准,我们希望这个分数越小越好,就是这个数会更加的稳定一些。
那怎么样去求解这个Obj让它更小?刚才我们已经找到了这个机制,也就是
O b j = ? 1 2 ∑ j = 1 T G j 2 H j + λ + γ T \begin{align*} Obj & = -\frac{1}{2} \sum_{j=1}^T \frac{G_j^2}{H_j + \lambda} + \gamma T \end{align*} Obj?=?21?j=1∑T?Hj?+λGj2??+γT?
这样Obj会比较好一点。那我们的树要去做分割,大家知道这个学习过程中的树是一点点长出来的,长出来的话叶子节点做分割就会成为一个父亲和孩子的一个结构。那要不要做分割的依据是啥?孩子的Obj应该要更小一点才会更好。所以你要去做的事情我们把它称为叫做一个Gain,Gain就是你分割的一个条件。
G a i n = 1 2 [ G L 2 H L + λ + G R 2 H R + λ ? ( G L + G R ) 2 H L + H R + λ ] ? γ \begin{align*} Gain = \frac{1}{2}\left[ \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda}\right ] - \gamma \end{align*} Gain=21?[HL?+λGL2??+HR?+λGR2???HL?+HR?+λ(GL?+GR?)2?]?γ?
这个式子中的几个部分如下:

Gain等于父亲啊减去孩子,也就是分割前的Obj减去分割后的左右Obj。如果说,父亲的Obj减去孩子的Obj等于Gain,那么Gain如果小于0,还要不要做分割?那么要记得,Gain<0, 那说明孩子比父亲还不稳定,那这个节点就不做分割,我们要找Gain>0的点。那Gain>0也有很多,我们要找其中最大的来做分割。这是XGBoost的一个过程。
那这里的可能性多不多我们怎么做?分裂节点的分裂,我们以这五个样本为例:
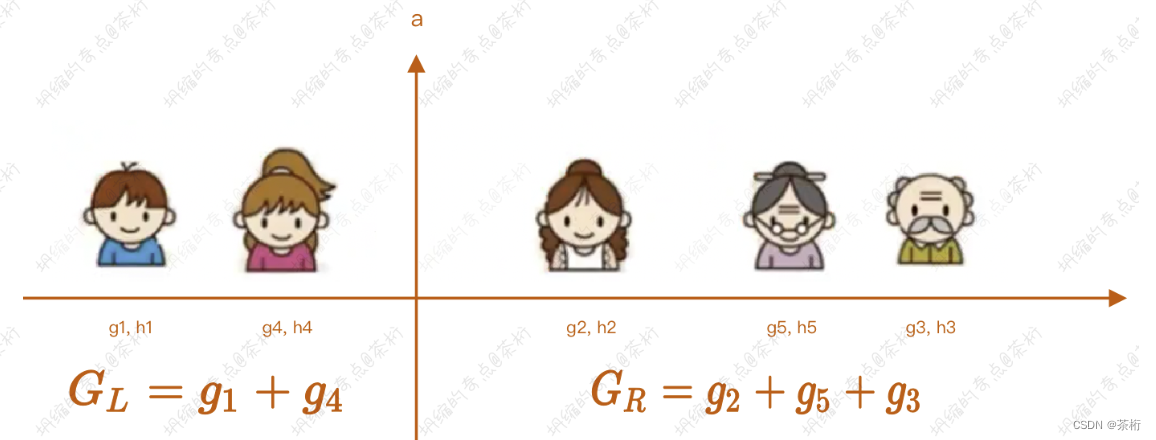
这是一个叶子节点,这叶子节点里面要去给它做分裂,先按照原来的g_i, 就是一阶的导数从小到大来做个排序,按照一定的顺序。
那g1, g4的顺序实际上就是g1比g4要小,后面也是。按照这个顺序来做排序,排序以后,我们现在切分有几种切分的方法?如果是5个样本的话,从最前面和最后面分割毫无意义,我们要做的是从中间将它们一分为二,那无非就是[[1,4], [2, 3], [3, 2], [4, 1]]。所以应该是四种结构。
我们有四种分裂的可能性,我们要找这种分裂的Obj最小的, 或者叫Gain最大的。四种结构我们要求4个Gain, 在四个里面去找到一种最大的来去做判断。
我们知道,我们的样本数有可能很多,一般机器学习有可能有上万个样本。一个节点,最开始原来样本假设有1万个,想想,1万个这样的样本要把它做划分的话,现在还是用从小到大给它规范好,这样的顺序来做划分有多少种划分方式呢?要计算1w-1次,接近1万次,9,999次。
这只是划分一次,决策树的划分不仅仅分裂一次,分裂完一次以后下个节点还可以再做分裂。所以每次来计算的话,这个计算量相当于是个for循环一样,计算量其实是蛮大的。
这是我们最开始的XGBoost的版本,对于它的节点划分来说我们要计算1w - 1次, 如果它的这个节点的样本是1w的话。

原始的XGBoost的计算量会比较大,这是在2014年的版本。XGBoost的原理在2014年提出来用的是一种贪心算法。这个贪心是从小到大的顺序来做了一个规范化,其实整个的顺序是有多种可能性的,我们是按照从小到大的顺序。然后去切的过程中,我们也只是看当下自有解,这是贪心计算方法。
但即使这种计算方法的计算量级也很多,在2016年作者就提出来一种改进的方式叫做histogram。

它用直方图,其目的就是把多个样本给它捆绑到一起。我们还是要做一个分裂的事情,再看刚才的结果,如果你在叶子节点上有1万个样本,原来是要切分出来9,999刀,现在把这1万个样本用绳子给它捆绑出来128个桶。桶就是一个最小的单位,把前面这些样本都拿绳子捆到一起,后面这个捆到一起,一共有多少桶?128个桶。
我们如果再去做切分的时候只能在桶与桶之间来做切分,那它的划分的样式有多少种?原来的1万要做9,999次的切分,现在128个桶,在做计算的时候就变成了127次。这种方式是种降维处理,有点类似于像聚类的方式,这样我们的计算量就大大缩减,所以他的计算的时间就会快很多。
这是XBGoost的一种近似的方法,近似的方法它不代表好,但是它是属于近似最优解,可以用更快的时间提升,基本上快几十倍还是有可能的。
以上就是XGBoost的原理,我们简单的再总结一下。
XGBoost是在GBDT多棵集成学习树上面做的优化。多棵学习树可以把它理解成model1+model2+…+modeln, 这是原来的集成学习的概念。XGBoost在原有基础上加了正则化项,正则化项的目的是防止过拟合。同时这个正则化项构造的很精巧,它用了一个公式,这个公式带进去以后经过一系列的转化,它的二阶项跟前面的1/2就消掉了。转化以后通过求偏导的方式可以把极值给求出来。前后相减的分裂过程是希望孩子的Obj更小。也就是说我们的父亲的Obj减去孩子的Obj等于Gain,每一项的话都可以进行一个求解,我们希望它的Gain变得更大一点。
那么怎么做分裂呢?就会有尝试多种分裂的方法,找到一种更最大的分裂方式。在这么多种分裂方法过程中采用的是贪心算法,1万个样本就要切1万减1刀。作者在2016年提出来了更快的方法,就是直方图的方法,这方法可以按照桶的个数来进行划分,所以它是一种近似的方式。
XGBoost算法的一些特点呢,就是讲树模型的复杂度加入到正则项中,从而避免过拟合,泛化性能好。其损失函数是用泰勒展开去完成的,用到了一阶和二阶导数,可以加快优化速度。它在寻找最佳分割点的时候,采用的是近似贪心算法,用来加速计算。那直方图还可以使用GPU来进行计算,GPU就可以采用并性化的方式来进行计算,所以速度就会比较快。XGBoost不仅支持CART作为基分类器,还支持线性分类器,在使用线性分类器的时候可以使用L1, L2正则化。
XGBoost有点是速度快、效果好、能处理大规模数据、支持自定义损失函数等,缺点就是算法参数过多,调参复杂,不适合处理超高维度特征数据。
XGBoost的通用参数:
booster[default=gbtree], 模型选择,gbtree或者gblinear。gbtree使用基于树的模型进行提升计算,gblinear使用线性模型进行提升计算。。silent[default=0],缄默方式,0表示打印运行时信息,1表示以缄默方式运行,不打印运行时信息。nthread[default=缺省值是当前系统可以获得的最大线程数],XGBoost运行时的线程数。num_feature, boosting过程中用到的特征个数,XGBoost会自动设置。eta[default=0.3], 为了防止过拟合,更新过程中用到的收缩步长。在每次提升计算之后,算法会直接获取新特征的权重。eta通过缩减特征的权重使提升计算过程更加保守,取值范围为[0, 1]。gamma[default=0], 分裂节点时,损失函数减小值只有大于等于gamma节点才分裂,gamma值越大,算法越保守,越不容易过拟合,但性能就不一定能保证,需要trade off, 取值范围[0, ∞]。max_depth[default=6], 树的最大深度,取值范围为[1, ∞], 典型值为3-10。min_child_weight[default=1],一个自己的所有观察值的最小权重和。如果新分裂的节点的样本权重和小于min_child_weight则停止分裂。这个可以用来减少过拟合,但是也不能太高,会导致欠拟合,取值范围为[0, ∞]。subsample[default=1], 构建每颗树对样本的采样率,如果设置成0.5, XGBoost会随机选择50%的样本作为训练集。colsample_bytree[default=1],列采样率,也就是特征采样率。lambda[default=1, alias:reg_lambda], L2正则化,用来控制XGBoost的正则化部分alpha[default=0, alias:reg_alpha],L2正则化,增加该值会让模型更加收敛。scale_pos_weight[default=1], 在类别高度不平衡的情况下,将参数设置大于0,可以加快收敛。
学习目标参数:
objective[default=reg:linear],定义学习目标,reg:linear,reg:logistic,binary:logistic,binary:logitraw,count:poisson,multi:softmax, multi:softprob,rank:pairwiseeval_metric,评价指标,包括rmse,logloss,error,merror,mlogloss,auc,ndcg,map等seed[default=0],随机数的种子dtrain,训练的数据num_boost_round,提升迭代的次数,也就是生成多少基模型early_stopping_rounds,早停法迭代次数evals:这是一个列表,用于对训练过程中进行评估列表中的元素。形式是evals = [(dtrain,‘train’),(dval,‘val’)]或者是evals = [(dtrain,‘train’)], 对于第一种情况,它使得我们可以在训练过程中观察验证集的效果verbose_eval,如果为True,则对evals中元素的评估输出在结果中;如果输入数字,比如5,则每隔5个迭代输出一次
nm -learning_rates:每一次提升的学习率的列表
我们看这个参数量还挺多的,XGBoost里面参数量确实还是比较多的,如果你用到的话可以回头再来看看我这篇文章,当作一个手册来看。默认情况下了,我会教给大家一些比较常见的参数设置,你直接用它就可以。
我这里还是给大家看一个示例
# 天猫用户复购预测(XGBoost使用示意)
X_train, X_valid, y_train, y_valid = train_test_split(train_X, train_y, test_size=.2)
# 使用XGBoost
model = xgb.XGBClassifier(
max_depth = 8, # 树的最大深度
n_estimators = 1000, # 提升迭代的次数,也就是生成多少基模型
min_child_weight = 300, # 一个子集的所有观察值的最小权重和
colsample_bytree = 0.8, # 列采样率,也就是特征采样率
subsample = 0.8, # 构建每颗树对样本的采样率
eta = 0.3, # eta通过缩减特征的权重使提升计算过程更加保守,防止过拟合
seed = 42 # 随机数种子
)
model.fit(X_train, y_train,
eval_metric='auc',
eval_set=[(X_train, y_train), (X_valid, y_valid)],
verbose=True,
# 早停法,如果auc在10epoch没有进步就stop
early_stopping_rounds = 10
)
model.fit(X_train, y_train)
prob = model.predict_proba(test_data)
比如我们现在创建好了一个model, XGBClassifier,创建好之后我们可以设置参数,比如一些树的深度等:
param = {
'boosting_type':'gbdt',
'objective':'binary:logistic', # 任务目标
'eval_metric':'auc', # 评估指标
'eta':0.01, # 学习率
'max_depth':15, #树最大深度
'colsample_bytree':0.8, #设置在每次迭代中使用特征的比例
'subsample': 0.9, #样本采样比例
'subsample_freq': 8, #bagging的次数
'alpha': 0.6, #L1正则
'lambda': 0, #L2正则
}
colsample和subsample, 这个分别代表我们的列采样和行采样。设置行采样和列采样是让我们每次训练的时候更加的快一点,更加的轻量一点。这两个参数和树的深度参数,这三个参数都是比较常见的需要设置的参数。此外我们还需要针对你的任务来去做设置任务目标。
我们以attraction这个题目为例可以看一看怎么用
train_data = xgb.DMatrix(X_train, label=y_train)
valid_data = xgb.DMatrix(X_valid, label=y_valid)
test_data = xgb.DMatrix(test)
model = xgb.train(param, train_data, evals=[(train_data, 'train'), (valid_data, 'valid')], num_boost_round = 10000, early_stopping_rounds=200, verbose_eval=25)
predict = model.predict(test_data)
test['Attrition']=predict # 转化为二分类输出
test['Attrition']=test['Attrition'].map(lambda x:1 if x>=0.5 else 0)
test[['Attrition']].to_csv('dataset/submit_lgb.csv')
原来的XGBoost还有两种版本, 一种版本的话是用它的DMatrix,这属于官方封装好的一个结构。 把原来切分好的数据集用DMatrix来做的一个封装,封装好以后再进行训练。所以它是属于一个自己的一个训练的一个数据结构,叫DMatrix。我们以前用训练的话一般用fit, 如果你用XGBoost官方版本的话,它写的是train,这是它的一个写法会稍微有一些区别。
带进去之后,其实后面都是调包的过程,train完以后predict,得到一个结果,最后把这个结果进行输出。
那我们来去用XGBoost来完成一下上节课我们完成的项目,首先还是数据的一些处理,这个和我们前几节课没有什么不同。主要就是我们要对一个参数进行设置;
param = {
'boosting_type': 'gbdt',
'objective': 'binary:logistic',
'eval_metric': 'auc',
'eta': 0.01,
'max_depth': 15,
'colsample_bytree': 0.8,
'subsample': 0.9,
'subsample_freq': 8,
'alpha': 0.6,
'lambda':0
}
这个就比我们之前调用其他模型来进行计算的参数量多了很多。然后我们用它官方的结构DMatrix:
train_data = xgb.DMatrix(X_train, label=y_train)
valid_data = xgb.DMatrix(X_valid, label=y_valid)
test_data = xgb.DMatrix(test)
这个套用就是把X_train,y_train给它放进去,它会封装一个自己的数据结构。所有样本都是一样,放进去训练的话就用自己的数据结构来去做训练。
model = xgb.train(param, train_data, evals=[(train_data, 'train'), (valid_data, 'valid')], num_boost_round=10000, early_stopping_rounds=200, verbose_eval=25)
param是前面设置好的,我们的训练的一些参数设置成一个字典,这是常见的一些配置。训练以后就可以拿这个模型去做预测得到一个预测结果,再把这个结果进行输出。
predict = model.predict(test_data)
test['Attrition'] = predict
print(predict)
---
[25] train-auc:0.98897 valid-auc:0.75885
...
[675] train-auc:1.00000 valid-auc:0.77299
[0.11253858 0.07342984 0.19541897 0.11211961 0.8137899 0.19079192
...
0.07080463 0.07864323 0.09115468 0.21122025 0.06211422 0.06264106]
我们打印的结果来看,发生了过拟合的情况。在做训练过程中,我们加了一个validation,现在train-auc和valid-auc都有一个评分。现在呢,训练集基本满分,但是验证集和它差别很大。
这种情况下我们就可以调整参数,来防止过拟合状况。那我们首当其冲应该想到的就是eta以及max_depth, 深度过大会造成过拟合,eta本来就是为了防止过拟合而在更新过程中用到的收缩步长。
在进行调整之后,过拟合状况就好多了:
[290] train-auc:0.91738 valid-auc:0.83852
下一节课,我们来看看Boosting的另外一个版本,微软出的LightBGM.
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!