随机微分方程数值实验 平衡法 Euler方法（matlab）

2023-12-28 14:26:16

题目：

计算带有乘性噪声的一维Ito型积分，即

$\begin{aligned} & d X(t)=\sigma X(t) d W(t) \\ & X(0)=x .\end{aligned}$

其真解为

$X(t)=x e^{-\frac{1}{2} \sigma^2 t+\sigma W(t)}$

一类平衡法数值格式为

$X_{k+1}=X_k+\sigma X_k \Delta_k W(h)+\sigma\left(X_k-X_{k+1}\right)\left|\Delta_k W(h)\right|$

Euler方法格式为

$\begin{aligned} & X_{K+1}=X_k+\sigma X_k \Delta_k \omega(h) \\ & X_0=x .\end{aligned}$

我们计算当$\sigma=4, x=1$时，比较两种方法的数值解逼近真解的情况。

程序：

randn('state',100)
sigma = 4;T = 1;Xzeros = 1;
N = 1.5e+5;
dt = 1/N;
dW = sqrt(dt)*randn(1,N);%Brownian increments
W = cumsum(dW);
%----------------true solution
Xtrue = Xzeros*exp(sigma*W-sigma^2/2*[dt:dt:T]);
R = 5;
Dt = R*dt;
L = N/R;
XE = zeros(1,L);
Xtemp = Xzeros;
%----------------Euler explicit method
for j = 1:L
    Winc = sum(dW(R*(j-1)+1:R*j));
    Xtemp = Xtemp+sigma*Xtemp*Winc;
    XE(j) = Xtemp;
end
%---------------The balanced method
XB = zeros(1,L);
Xtemp = Xzeros;
for j = 1:L
    Winc = sum(dW(R*(j-1)+1:R*j));
    Xtemp = ((1+sigma*abs(Winc))*Xtemp+sigma*Xtemp*Winc)/(1+sigma*abs(Winc));
    XB(j) = Xtemp;
end
figure
plot([(0:Dt:T)],[Xzeros,XE],'r-*');
hold on;
plot([0:dt:T],[Xzeros Xtrue],'k--');
legend('显式Euler数值解','真解');
figure
plot([(0:Dt:T)],[Xzeros,XB],'y+'),
hold on
plot([0:dt:T],[Xzeros Xtrue],'k--');
legend('平衡法数值解','真解');
erro=max(abs([Xzeros,XE]-[Xzeros,XB]))

结果：

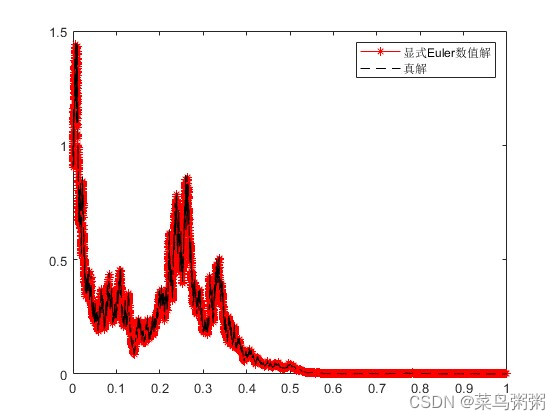
平衡方法和Euler方法的数值解图像和真解图像基本吻合，通过这两种方法得到数值解相差0.0830。

文章来源:https://blog.csdn.net/2301_76767110/article/details/135219965
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。