特征工程（特征提取&数据预处理）

2024-01-08 18:52:39

?一、特征提取

在房价模型的例子中，我们提取房子的长度（frontage）和宽度（depth）作为特征之一。并得到初步的特征方程：

frontage=x_{1},depth=x_{2}

f_{\vec{w},b}(\vec{x})=w_{1}x_{1}+w_{2}x_{2}+b

然而我们知道，房屋面积可以表示为：area = depth*frontage。用土地面积作为独立特征可以更好地预测价格，所以我们将area作为新的特征提取出来并定义新的特征方程:

area = x_{3} = x_{1}*x_{2}

f_{\vec{w},b}(\vec{x})=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+b

(大家可能会觉得变量太多。其实现在只是建立了一个初步的模型，在之后使用决策树、正则化等算法可以减少特征数量）

二、特征缩放（数据预处理）

1.1了解特征缩放

首先从吴恩达老师给的例子开始讲解：

?以房价为例：

假设房子价格只受占地面积（x_{1}）和卧室数量（x_{2}）影响,我们可以得到如下模型：

\hat{price}=w_{1}x_{1}+w_{2}x_{2}+b

假设已知一组数据 {House:x_{1}?=2000,?x_{2}=5,price=$500k} :

  • 我们如果假设x_{1}的影响因素较大，便假设w_{1}=50,w_{2}=0.1,b=50k,得到price=$100,050,500，与实际值相差甚远
  • 我们如果假设x_{2}的影响因素较大，便假设w_{1}=0.1,w_{2}=50,b=50k,得到price=$500,000,比较接近事实。

对应到表格和坐标轴上我们可以得到以下信息：

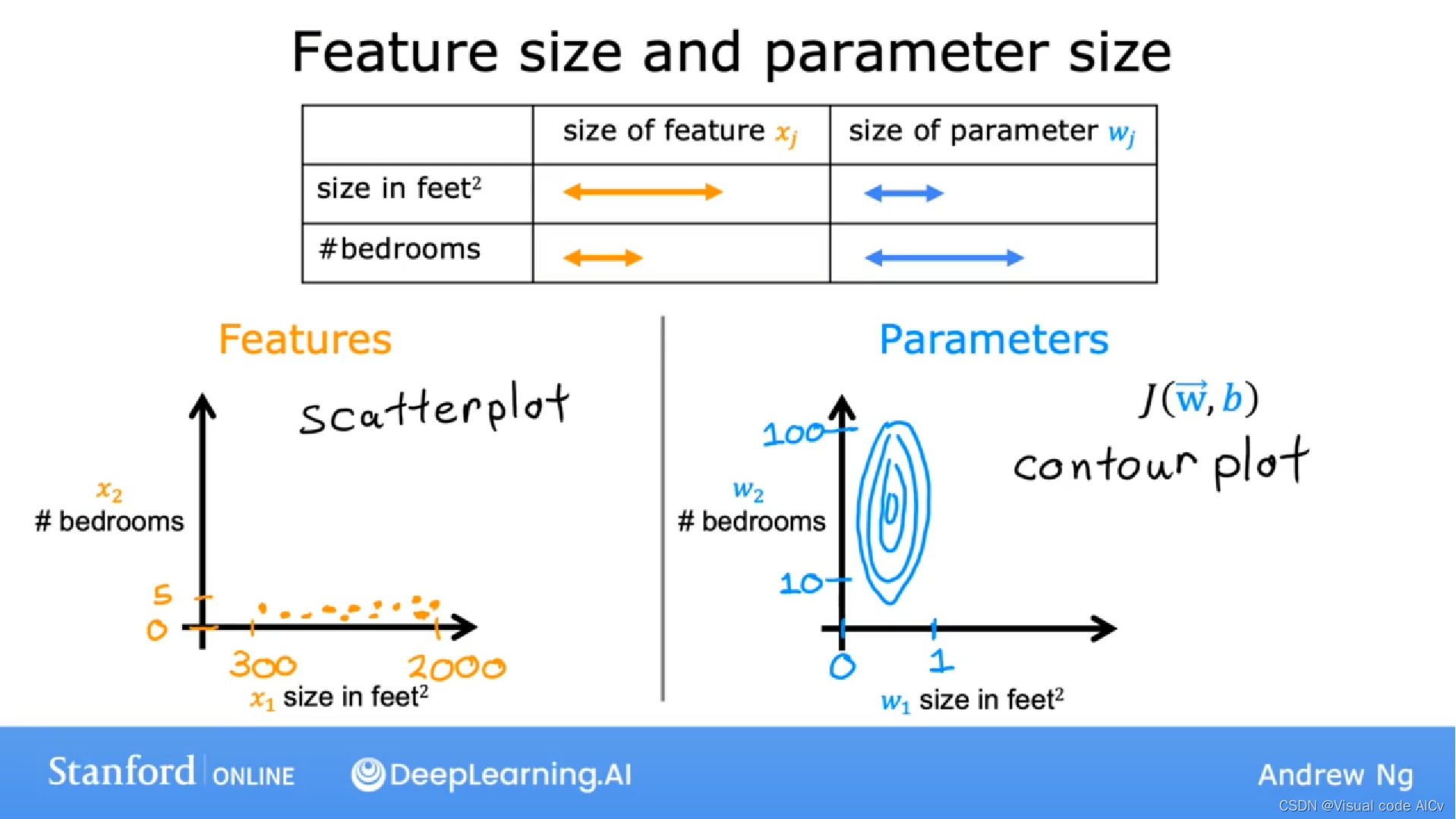
图注：

  • 左侧为数据集在坐标轴中的展示，横坐标为占地面积，纵坐标为卧室数量。
  • 右侧为损失函数（cost function）在坐标轴中的展示，横坐标为房间尺寸，纵坐标为卧室数量。中心点为梯度下降法应该指向的最低点。
  • 我们可以看出，在数据集中size的变化范围极大，而bedrooms的数量范围极小。而在损失函数的图中，横坐标的值却很小，纵坐标的值却很大。说明w1非常小的变化会对价格产生非常大的影响，这对损失函数J（w1,w2,b)影响非常大。

????????假设我们按照真实场景将卧室数量的取值范围定为(0,5)，而占地面积的取值范围定为(300,2000)；我们会发现，得到的图以及对应的损失函数图如下图中第一行所示。梯度下降法会如同图中的箭头一般来回弹跳缓慢地指向最低点。

? ? ? ? 如果我们缩放特征（直观来看就是改变x_{1}和x_{2}的取值范围）我们发现将如第二行一样，数据集的点在坐标系上分布均匀，而损失函数图也如同正同心圆，不那么高瘦或矮胖。梯度下降法可以找到一条更加直接的通向最低点的路径。

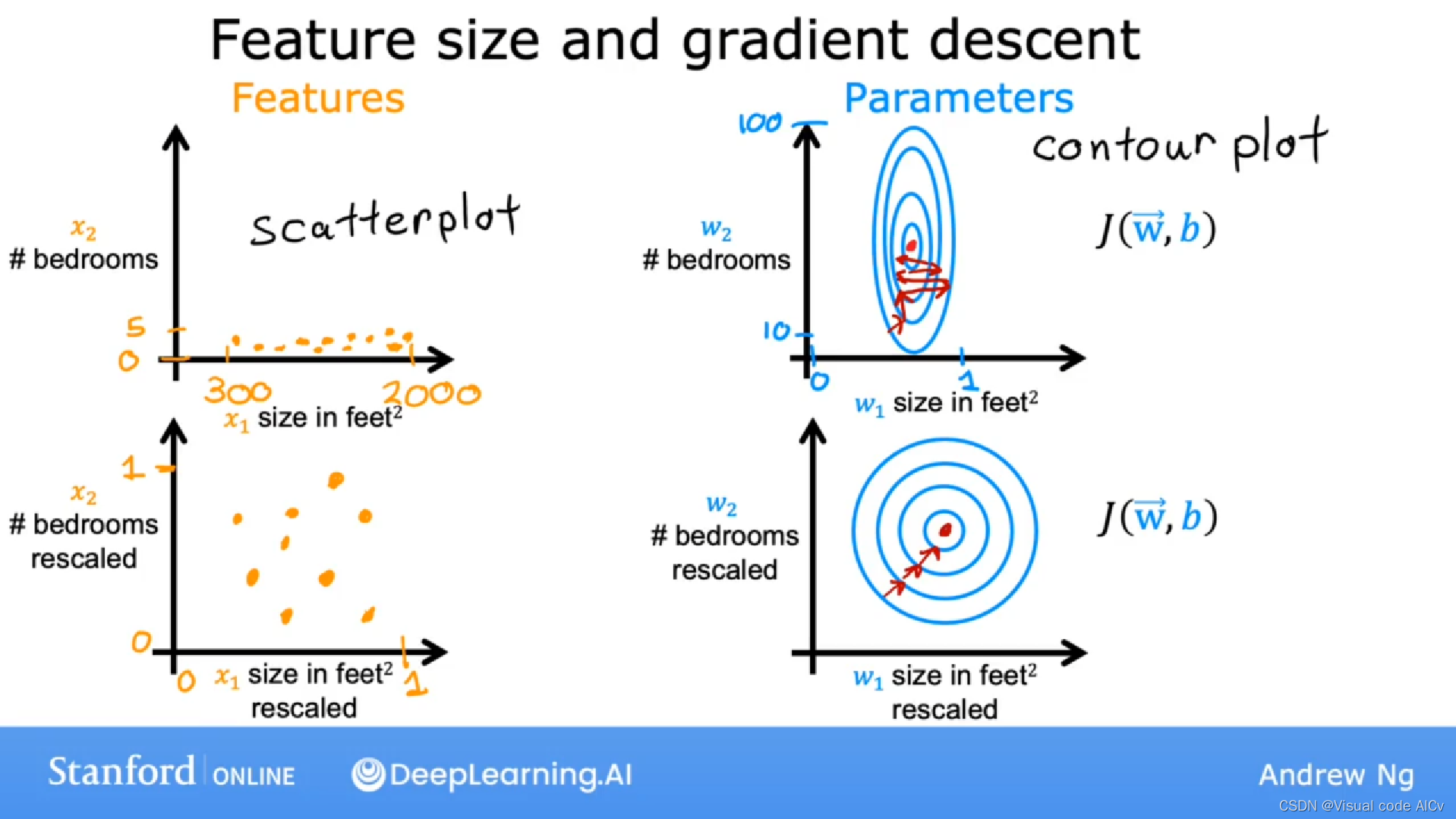
? 结论：由此我们得到了特征缩放是通过根据一定规则重新缩放特征变量（如x_{1}和x_{2}），使它们都具有可比较的取值范围，由此提高梯度下降运行的速度。

1.2归一化——进行特征缩放的主要方法

归一化:一种数据预处理技术，旨在将数值型数据缩放到特定的范围内，通常是[0, 1]或者[-1, 1]。归一化的目的是消除不同特征之间的量纲差异，使得不同特征之间具有可比性，有利于机器学习模型的训练和收敛。

Z-score均值归一化公式：(假设有多个因素，每个因素对应一个数据集）

x_{i} = \frac{x_{i} - \mu_{i}}{\sigma_{i}}(\sigma_{i}=x_{max}-x_{min})

其中，( x_{i}?) 是原始数据，( \mu_{i} ) 是原始数据的均值，( \sigma_{i} ) 是原始数据的标准差。

同样以上面房价模型为例子：

?????????假设数据样本计算出的bedrooms的均值为1.4，size的均值为450；则得到下图中的特征因素（feature）的新范围和图像：

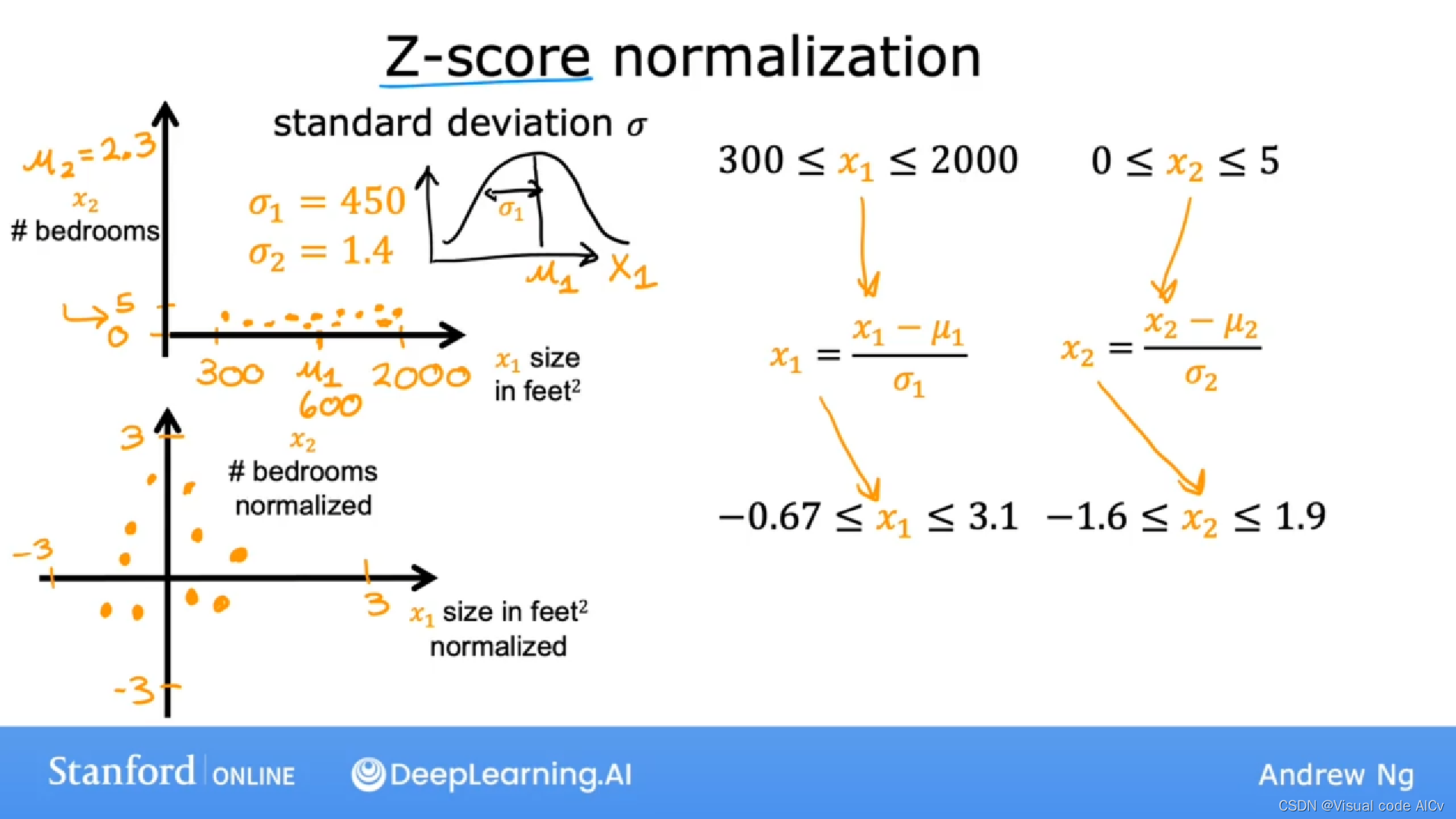
使用归一化的情景：

归一化的目标是将特征x_{i}的范围限制在（-1,1），（-3,3），（-0.3,0.3）这样的范围。像是范围太小或太大的特征就需要进行重新缩放。

文章来源:https://blog.csdn.net/m0_65995252/article/details/135418921
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。