深入理解强化学习——马尔可夫决策过程：价值迭代-[价值迭代算法]

分类目录：《深入理解强化学习》总目录

文章《深入理解强化学习——马尔可夫决策过程：价值迭代-[最优性原理]》和文章《深入理解强化学习——马尔可夫决策过程：价值迭代-[确认性价值迭代]》介绍了价值迭代的基础知识，本文将介绍价值迭代算法。

价值迭代算法的过程如下：

价值迭代算法
（ 1 ） 初始化：令$k=1$，$?s:V_0(s)=0$
（ 2 ） for $k=1:H$，$H$为使$V(s)$收敛所需的迭代次数
（ 3 ） $?s:Q_{k+1}(s,a)=R(s,a)+\gamma {\sum }_{s^{\prime }\in S}p(s^{\prime }|s,a)V_k(s^{\prime })$
（ 4 ） $?s:V_{k+1}(s)={\max }_a{Q}_{k+1}(s,a)$
（ 5 ） $k=k+1$
（ 6 ） 在迭代后提取最优策略：$\pi (s)=\arg {\max }_a[R(s,a)+\gamma {\sum }_{s\in S}p(s^{\prime }|s,a)V_{H+1}(s^{\prime })]$

我们使用价值迭代算法是为了得到最佳的策略$\pi$。我们可以使用文章《深入理解强化学习——马尔可夫决策过程：价值迭代-[确认性价值迭代]》中的式子进行迭代，迭代多次且收敛后得到的值就是最佳的价值。

价值迭代算法开始的时候，把所有值初始化，接着对每个状态进行迭代。 我们把$Q_{k+1}(s,a)=R(s,a)+\gamma {\sum }_{s^{\prime }\in S}p(s^{\prime }|s,a)V_k(s^{\prime })$代入式$V_{k+1}(s)={\max }_a{Q}_{k+1}(s,a)$，就可以得到文章《深入理解强化学习——马尔可夫决策过程：价值迭代-[确认性价值迭代]》中的式子。因此，我们有了上两式后，就不停地迭代，迭代多次后价值函数就会收敛，收敛后就会得到$V^{?}$。我们有了$V^{?}$后，一个问题是如何进一步推算出它的最佳策略。我们可以直接用$\arg \max$ 操作来提取最佳策略。我们先重构Q函数，重构后，每一列对应的Q值最大的动作就是最佳策略。这样我们就可以从最佳价值函数里面提取出最佳策略。 我们只是在解决一个规划的问题，而不是强化学习的问题，因为我们知道环境如何变化。

价值迭代做的工作类似于价值的反向传播，每次迭代做一步传播，所以中间过程的策略和价值函数 是没有意义的。而策略迭代的每一次迭代的结果都是有意义的，都是一个完整的策略。下图所示为一个可视化的求最短路径的过程，在一个网格世界中，我们设定了一个终点，也就是左上角的点。不管我们在哪一个位置开始，我们都希望能够到达终点（实际上这个终点在迭代过程中是不必要的，只是为了更好地演示）。价值迭代的迭代过程像是一个从某一个状态（这里是我们的终点）反向传播到其他各个状态的过程，因为每次迭代只能影响到与之直接相关的状态。 让我们回忆一下最优性原理定理：如果我们某次迭代求解的某个状态$s$的价值函数$V_{k+1}(s)$是最优解，它的前提是能够从该状态到达的所有状态$s‘’$都已经得到了最优解；如果不是，它所做的只是一个类似传递价值函数的过程。

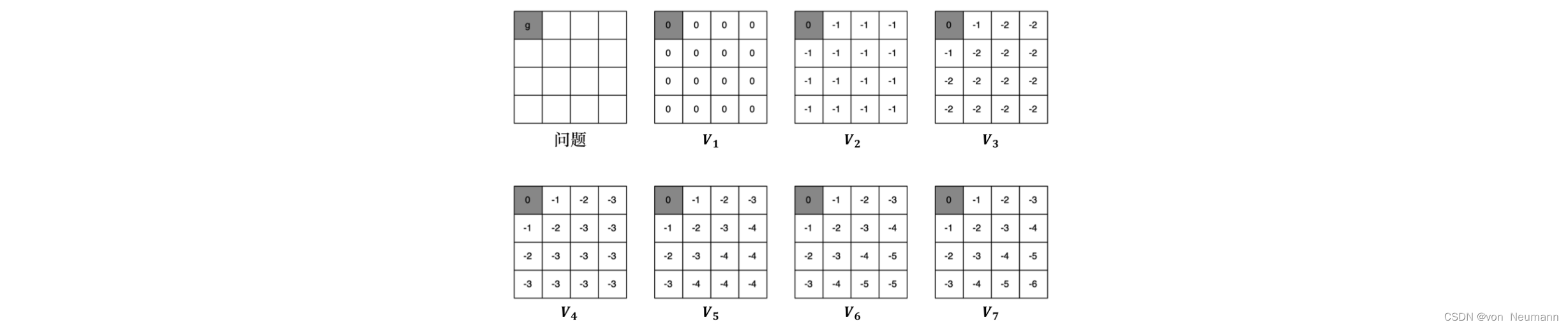
如上图所示，实际上，对于每一个状态，我们都可以将其看成一个终点。迭代由每一个终点开始，我们每次都根据贝尔曼最优方程重新计算价值。如果它的相邻节点价值发生了变化，变得更好了，那么它的价值也会变得更好，一直到相邻节点都不变。因此，在我们迭代到$V_7$之前，也就是还没将每个终点的最优的价值传递给其他的所有状态之前，中间的几个价值只是一种暂存的不完整的数据，它不能代表每一个状态的价值，所以生成的策略是没有意义的策略。价值迭代是一个迭代过程，上图可视化了从$V_1$到$V_7$每一个状态的价值的变化。而且因为智能体每走一步就会得到一个负的价值，所以它需要尽快地到达终点，可以发现离它越远的状态，价值就越小。$V_7$收敛过后，右下角的价值是$?6$，相当于它要走6步，才能到达终点。智能体离终点越近，价值越大。当我们得到最优价值后，我们就可以通过策略提取来得到最佳策略。

参考文献：
[1] 张伟楠, 沈键, 俞勇. 动手学强化学习[M]. 人民邮电出版社, 2022.
[2] Richard S. Sutton, Andrew G. Barto. 强化学习（第2版）[M]. 电子工业出版社, 2019
[3] Maxim Lapan. 深度强化学习实践（原书第2版）[M]. 北京华章图文信息有限公司, 2021
[4] 王琦, 杨毅远, 江季. Easy RL：强化学习教程 [M]. 人民邮电出版社, 2022