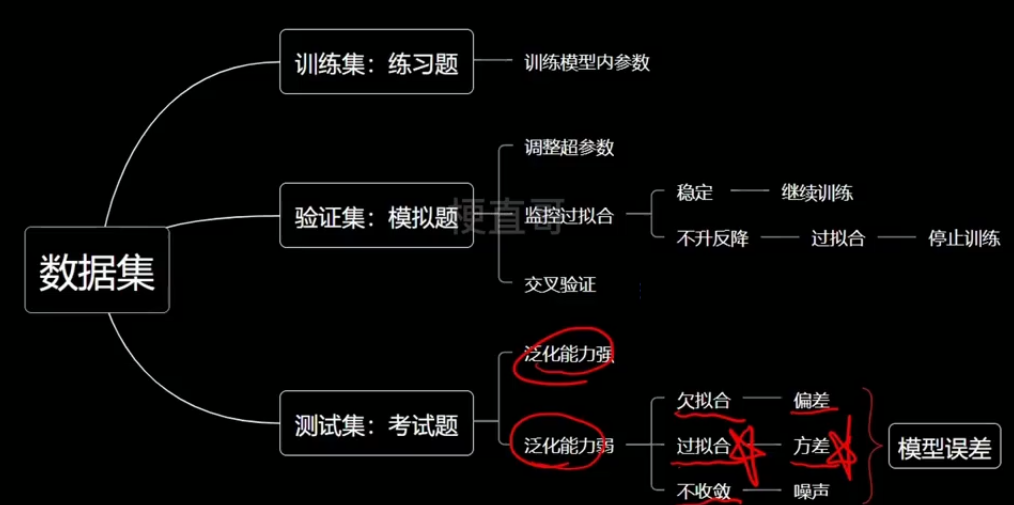
机器学习 | 过拟合与正则化、模型泛化与评价指标
?一、过拟合与正则化
1、多项式逼近思想
????????任何函数都可以用多项式来表示。
????????![]()
??????? 举个栗子 ~
??????? 比如说 泰勒公式
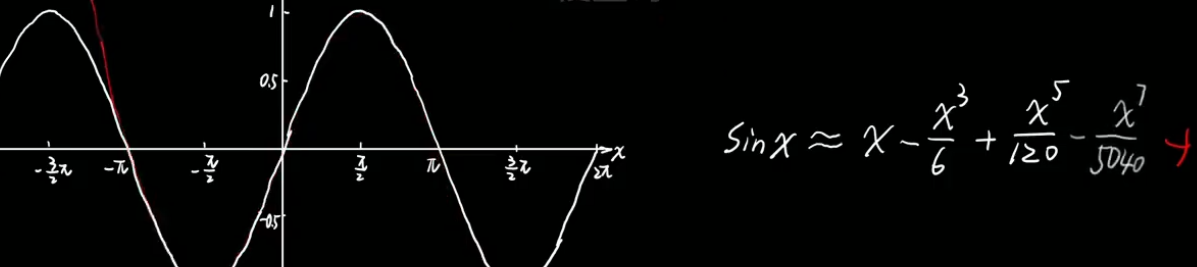
??????? ??????? 若要拟合sinx,泰勒认为仿造一条曲线,首先要保证在原点重合,之后在保证在这个点处的倒数相同,导数的倒数相同。
??????????????? 高次项引入了更多的弯折,;同时使得相似范围越来越大。
????????????????
2、过拟合的真相
??????? 过拟合的真相 —— 高次项过多。
??????? 为了防止过拟合,就要控制高次项的个数 n ,可以通过控制wn的个数来实现。
??????? 所以解决过拟合问题就变成了让 w向量中 项的个数最小化的问题。
????????写成数学语言: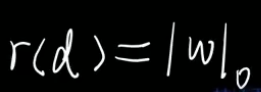
??????? —— 这就是数学中 零范数(norm) 的概念。
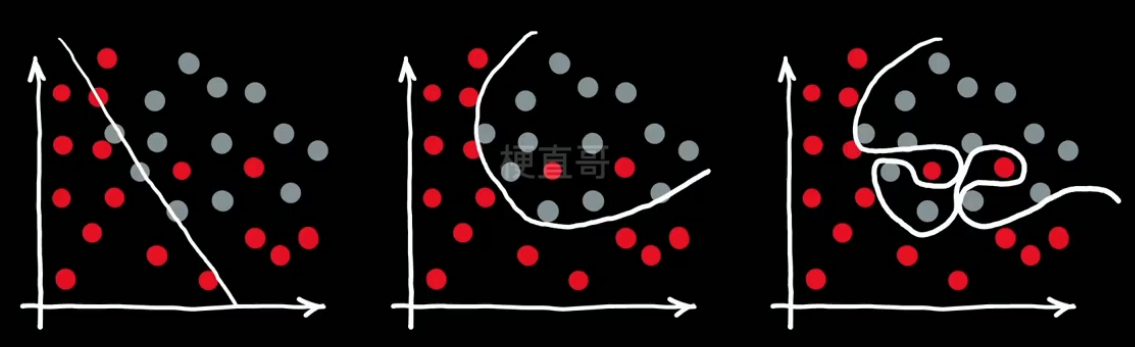
??????????????? 它就类似向量中长度的概念。可以理解为下图中分类线的长度。
????????????????
3、正则化与相似概念对比
- 其中 φ 为正则化项,λ为他的系数
- 最小化损失函数的同时尽量减少参数项的个数

- 甭管是几范数,都可以理解成长度 ~


 ????????
????????
4、L1正则化空间解释 LASSO回归
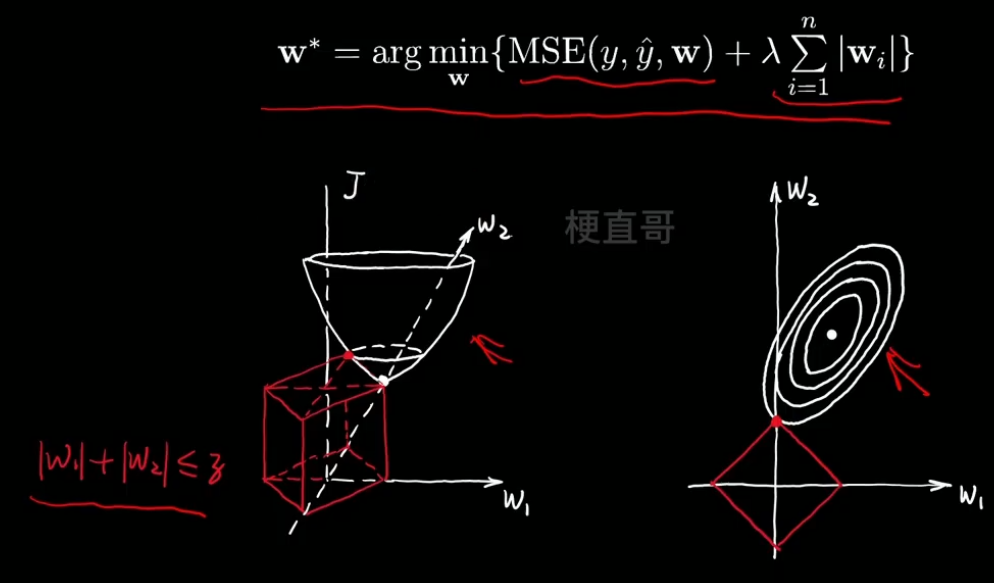
??????? 左边图即为G损失函数在特征空间中的三维分布,红色即为正则化项的分布。
??????? 投影到右边图中,当没有正则项时,我们找的是这个漏斗的最低点。
??????? 现在要同时满足两者都达到最小,即红色交点,而这个点恰巧 w1=0。
??????????????? 换句话说,L1正则项(一次正则项)可以降低参数的维度。
????????
5、L2正则化空间解释 Ridge岭回归
??????? 与L1正则化不同,
??????? 等值线与圆的任何部分相交的概率都是相同的,所以交点会尽量靠近坐标轴中间的位置。
????????这使得L2正则,相对而言,是鼓励产生小而分散的权重,考虑更多的特征,而不仅仅是依赖某几个特征,因此可以增强模型泛化能力。
??????? 此外,因为二次正则项处处可导,这使得计算更加方便。
????????
??????? 总的来说,正则项相当于给最小化增加了空间的约束,限制了模型的复杂度,因而可以很好解决过拟合问题。
二、模型泛化
??????? 泛化能力:机器学习算法对新鲜样本的适应能力
??????? 奥卡姆剃刀法则:能简单别复杂
??????? 泛化理论:衡量模型复杂度
??????? Generalization:可以理解为一般化
三、评价指标
1、混淆矩阵、精准率、召回率
??????? 以检测核酸为例:
????????
??????? 评价指标:
????????
??????? F1 Score
????????
????????
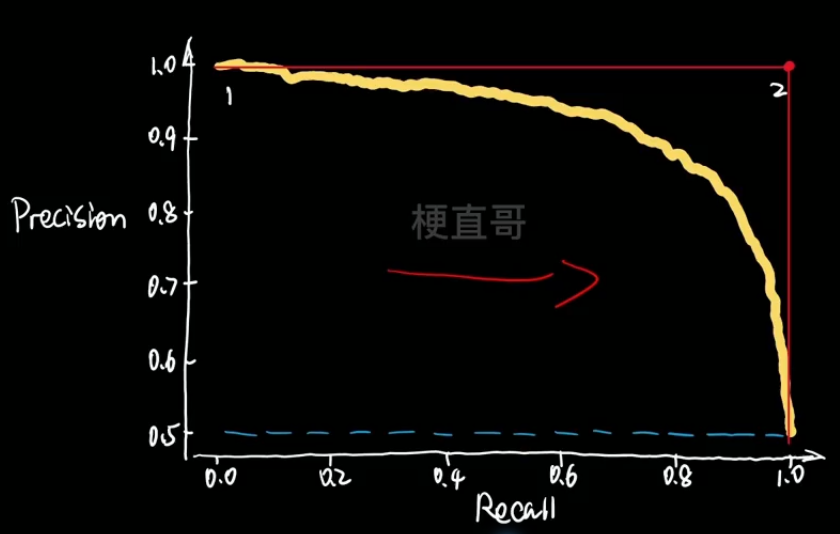
2、PR曲线与ROC曲线
????????
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!