【三维重建】对极几何

2023-12-14 21:08:17

极几何描述了同一场景或者物体的两个视点图像间的几何关系

可以发现Ｐ在左右相机的投影点一定在各自的极线上，如果求出极线就能缩小求解对应点的范围。

本质矩阵对规范化摄像机拍摄的两个视点图像间的极几何关系进行代数描述

规范化相机指的是相机的内参矩阵为一个单位矩阵

P'=\begin{bmatrix} x\\y \\ z \end{bmatrix}=\begin{bmatrix} 1 &0 & 0 & 0\\ 0&1 &0 &0 \\ 0& 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x\\y \\ z \\ 1 \end{bmatrix} \ \ P'=MP?????

设p'^*是p'在O_1坐标系下的坐标，则：

p'=Rp'^*+T \rightarrow p'^*=R^Tp'-R^TT(R^{-1} = R^T)

因此，p'在O_1坐标系下的坐标为　R^Tp'-R^TT

同理：O_2在O_1坐标系下的坐标为　-R^TT

得到两个向量　O_1p' \ , O_1O_2

O_1p' \times O_1O_2 = R^TT \times (R^Tp'-R^TT)=R^TT \times R^Tp' （垂直于极平面）

[R^TT \times R^Tp']^T \cdot p = 0

a \times b 可以写成一个矩阵乘积的形式，比如：

a = (x_1,y_1,z_1),b=(x_2,y_2,z_2)

a \times b = (y_1z_2-z_1y_2,z_1x_2-x_1z_2,x_1y_2-y_1x_2)\\ = \begin{bmatrix} 0& -z_1 &y_1 \\ z_1&0 &-x_1 \\ -y_1&x_1 &0 \end{bmatrix}\begin{bmatrix} x_2\\y_2 \\ z_2 \end{bmatrix}

因此，

[R^TT \times R^Tp']^T \cdot p = [T \times p']^TRp=[T_xp']^TRp \\ \\ =p'^TT_x^TRp=p'^TT_xRp=p'^T[T \times R]p = 0

（　T_x　是一个秩为２的对称矩阵）

E = T \times R = T_{\times}R

E就是本质矩阵，描述了规范化摄像机下两个视点的关系。

p^T \cdot l = 0 ,\ p'^TEp =0\rightarrow l =E^Tp' \\ p'^T \cdot l' = 0 ,\ p'^TEp =0\rightarrow l' =Ep

e也是极线ｌ上的点，所以

l^Te = p'^TEe=0\rightarrow Ee =0

基础矩阵对一般的透视摄像机的两个视点的图像间的极几何关系进行代数描述

核心思想是将一般相机下的p,p'，变成规范化相机下的p,p'

p=K[I\ O]P\rightarrow K^{-1}p=K^{-1}K[I \ O]P\rightarrow \begin{bmatrix} 1 &0 &0 &0 \\ 0& 1& 0&0 \\ 0 & 0&1 & 0 \end{bmatrix}P

let \ \begin{bmatrix} 1 &0 &0 &0 \\ 0 & 1 & 0 &0 \\ 0 & 0 & 1 & 0 \end{bmatrix}P = p_c\rightarrow p_c = K^{-1}p \ , p_c '= K'^{-1}p'

p_c',p_c符合规范换相机要求，因此：

p_c'Ep_c=p_c'^T[T_{\times}]Rp_c=(K'^{-1}p' )^T [T_{\times}]RK^{-1}p \\ \\ =p'^TK'^{-T}[T_{\times}]RK^{-1}p = 0

let F=K'^{-T}[T_{\times}]RK^{-1},\ p'^TFp=0

F就是基础矩阵，反映了一般相机下，两视点间的关系。

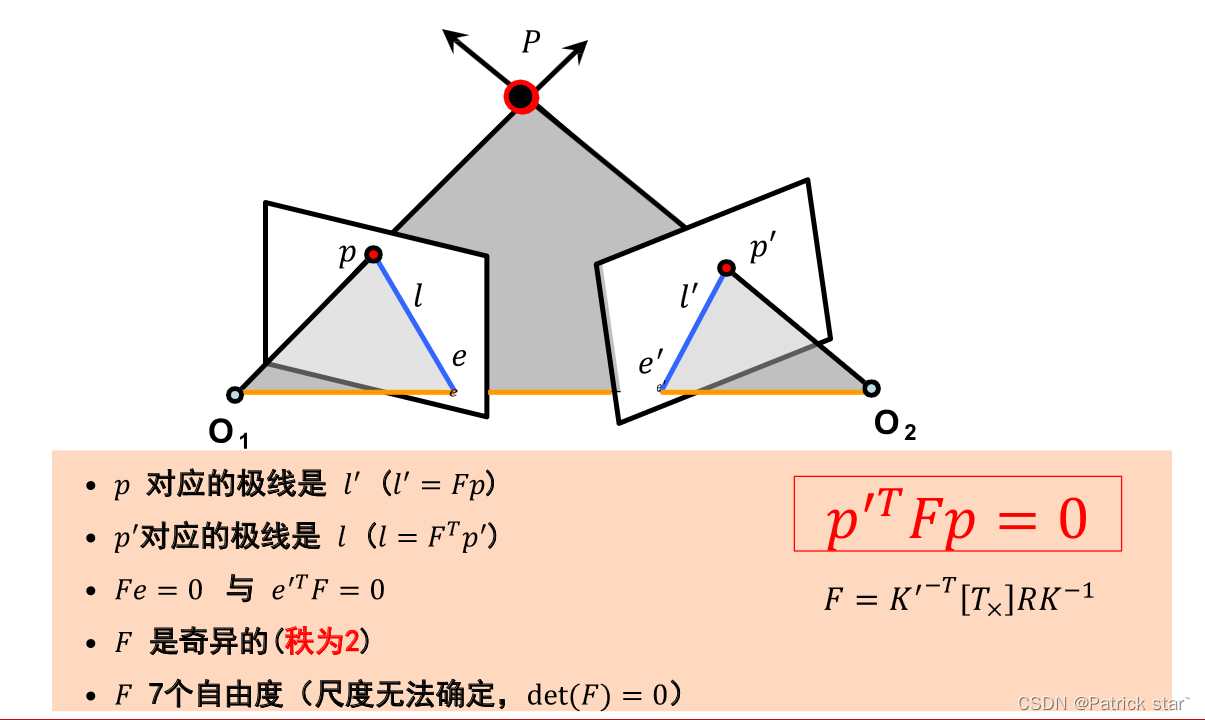
求解基础矩阵

用对应点求解Ｆ

求出的\hat{F}往往是满秩的，而我们所要求的基础矩阵秩为２

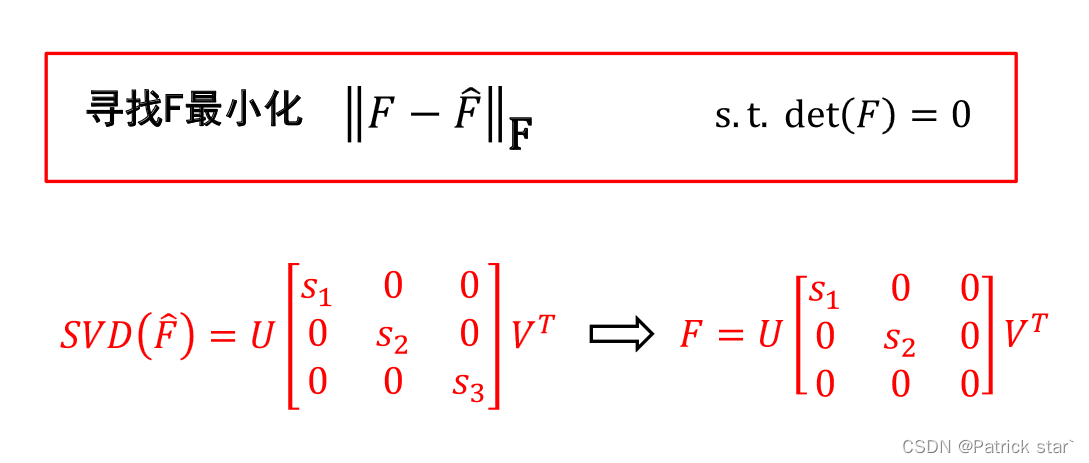
单应性矩阵

　

如果采集到的对应点在同一平面，两个视点间的对应关系用单应性矩阵表示

M = K(I \ O),\ M' = K'(I\ O),\ P= (\tilde{P^T},1)^T \\ \\ p = M\begin{pmatrix} \tilde{P}\\1 \end{pmatrix} =K \tilde{P} \\ \\ p' = M'\begin{pmatrix} \tilde{P}\\1 \end{pmatrix}=K'(R \ t)\begin{pmatrix} \tilde{P} \\1 \end{pmatrix}=K'(R \tilde{P} + t)

n^T \tilde{P} = d \rightarrow n^T \tilde{P} / d = 1 \\ \\ let \ n / d = n_d , n_d^T \tilde{P} = 1

?p'=K'(R\tilde{P} + t \cdot n_d^T \tilde{P}) = K'(R + t \cdot n_d^T)\tilde{P} =K'(R + t \cdot n_d^T)K^{-1}p

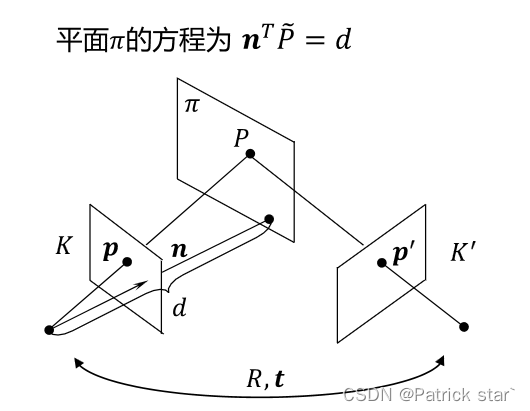
本质矩阵 H = K'(R + t \cdot n_d^T)K^{-1}

参考内容：计算机视觉之三维重建（深入浅出SfM与SLAM核心算法）—— 4. 三维重建基础与极几何_哔哩哔哩_bilibili

文章来源:https://blog.csdn.net/holle_world_ldx/article/details/134811917
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。