训练神经网络(上)激活函数

本文介绍几种激活函数,只作为个人笔记.观看视频为cs231n

前言

一、Sigmoid函数

二、tanh函数

三、ReLU函数

四、Leaky ReLU函数

五、ELU函数

六.在实际应用中寻找激活函数的做法

总结

---

前言

激活函数是用来加入非线性因素的，提高神经网络对模型的表达能力，解决线性模型所不能解决的问题。

一、Sigmoid函数

这个函数大家应该熟悉在逻辑回归中曾用到这个sigmoid函数

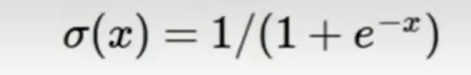
这个函数可以将负无穷和正无穷映射到(0,1)上即

如果你有一个非常大的输入值那么就会接近于1

如果你有一个非常小的输入值那么就会接近于0

但这个函数会出现几个问题.

1.饱和神经元使得梯度消失

梯度下降法（以及相关的L-BFGS算法等）在使用随机初始化权重的深度网络上效果不好的技术原因是：梯度会变得非常小。具体而言，当使用反向传播方法计算导数的时候，随着网络的深度的增加，反向传播的梯度（从输出层到网络的最初几层）的幅度值会急剧地减小。结果就造成了整体的损失函数相对于最初几层的权重的导数非常小。这样，当使用梯度下降法的时候，最初几层的权重变化非常缓慢，以至于它们不能够从样本中进行有效的学习。这种问题通常被称为“梯度的弥散”.

从图中我们可以看到在图的两端的梯度越来越接近为0,经过链式法则后会让梯度流消失,这样在使用梯度下降法时参数会更新的非常缓慢,也就是上面所说的梯度弥散问题.

2.sigmoid函数是一个非零中心的函数

神经网络：激活函数非0中心导致的问题 - 知乎 (zhihu.com)

这里有篇知乎文章可以帮助大家更好理解,其实大家把公式推一下就可以理解了,最后导致所有的w参数只能每次沿正或者负方向变换就导致,以z字形逼近最优参数,导致梯度下降的收敛较慢.

3.对e指数的计算量有一点大

二、tanh函数

双曲正切函数是双曲函数的一种。双曲正切函数在数学语言上一般写作 tanh。它解决了Sigmoid函数的不以0为中心输出问题，然而，梯度消失的问题和幂运算的问题仍然存在.

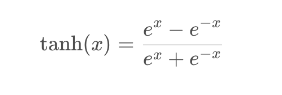
三、ReLU函数

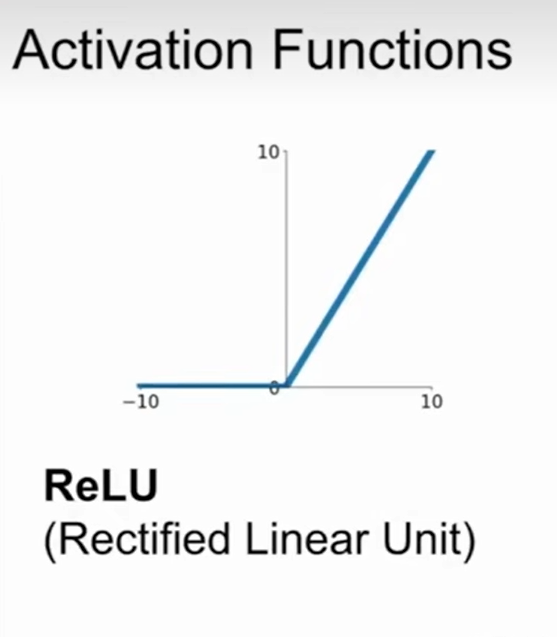
ReLU，全称为：Rectified Linear Unit，是一种人工神经网络中常用的激活函数，通常意义下，其指代数学中的斜坡函数，即

ReLU函数的优点

1. SGD算法的收敛速度比sigmoid和 tanh 快;(梯度不会饱和，解决了梯度消失问题)
2. 计算复杂度低，不需要进行指数运算;
3. 适合用于后向传播。

ReLU函数的缺点

1. ReLU的输出不是zero-centered;
2. ReLU在训练的时候很"脆弱”，一不小心有可能导致神经元"坏死”。举个例子:由于RelU在x<0时梯度为0，这样就导致负的梯度在这个ReLU被置零，而且这个神经元有可能再也不会被任何数据激活。如果这个情况发生了，那么这个神经元之后的梯度就永远是0了，也就是ReLU神经元坏死了，不再对任何数据有所响应。实际操作中，如果你的learning rate很大，那么很有可能你网络中的40%的神经元都坏死了。当然，如果你设置了一个合适的较小的learning rate，这个问题发生的情况其实也不会太频繁。，DeadReLU Problem （神经元坏死现象)︰某些神经元可能永远不会被激活，导致相应参数永远不会被更新(在负数部分，梯度为0)。产生这种现象的两个原因:参数初始化问题; learning rate太高导致在训练过程中参数更新太大。解决方法:采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。
3. ReLU不会对数据做幅度压缩，所以数据的幅度会随着模型层数的增加不断扩张。
   ?

四、Leaky ReLU函数

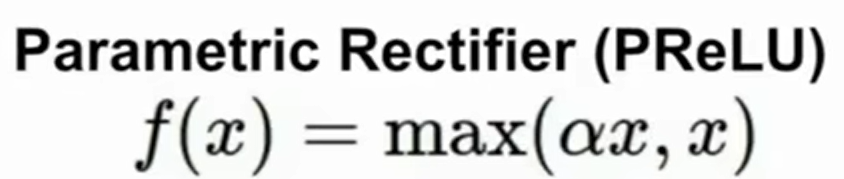
Leaky ReLU函数通过把x xx的非常小的线性分量给予负输入0.01 x 来调整负值的零梯度问题。
Leaky有助于扩大ReLU函数的范围，通常α 的值为0.01左右。
Leaky ReLU的函数范围是负无穷到正无穷。

五、ELU函数

1. 没有Dead ReLU问题，输出的平均值接近0，以0为中心。
2. ELU 通过减少偏置偏移的影响，使正常梯度更接近于单位自然梯度，从而使均值向零加速学习。
3. ELU函数在较小的输入下会饱和至负值，从而减少前向传播的变异和信息。
4. ELU函数的计算强度更高。与Leaky ReLU类似，尽管理论上比ReLU要好，但目前在实践中没有充分的证据表明ELU总是比ReLU好。

六.在实际应用中寻找激活函数的做法

---

总结

本文介绍了神经网络的几种激活函数,后面还会更新剩余几个激活函数,大致了解一下每个函数的图像的样子,以及在实践中我们一般寻找激活函数的做法.