2023-12-18 最大二叉树、合并二叉树、二叉搜索树中的搜索、验证二叉搜索树
2023-12-18 23:34:56
654. 最大二叉树

核心:记住递归三部曲,一般传入的参数的都是题目给好的了!把构造树类似于前序遍历一样就可!就是注意单层递归的逻辑!
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
# 递归三部曲
if not nums:
return
max_ = max(nums)
max_index = nums.index(max_)
root = TreeNode(max_)
root.left = self.constructMaximumBinaryTree(nums[:max_index])
root.right = self.constructMaximumBinaryTree(nums[max_index + 1:])
return root
def constructMaximumBinaryTree2(self, nums: List[int]) -> Optional[TreeNode]:
# 递归的三部曲 1.确定参数以及返回值--传入数组,输出节点 2.结束递归条件--如果数组len==1说明遍历到叶子节点了 3.单层逻辑--找到最大值以及最大值的下标
if len(nums) == 1:
return TreeNode(nums[0])
node = TreeNode(0)
max_numb = 0
max_index = 0
for i in range(len(nums)):
if nums[i] > max_numb:
max_index = i
max_numb = nums[i]
node.val = max_numb
# 判断下标值是否大于0 说明是否有左子树
if max_index > 0:
new_list = nums[:max_index]
node.left = self.constructMaximumBinaryTree(new_list)
if max_index < len(nums) - 1:
new_list = nums[max_index + 1:]
node.right = self.constructMaximumBinaryTree(new_list)
return node
617. 合并二叉树
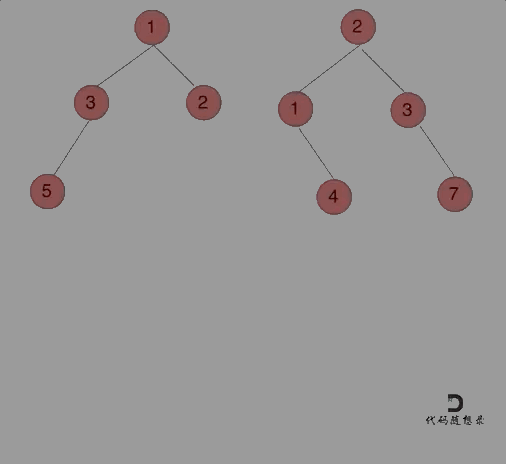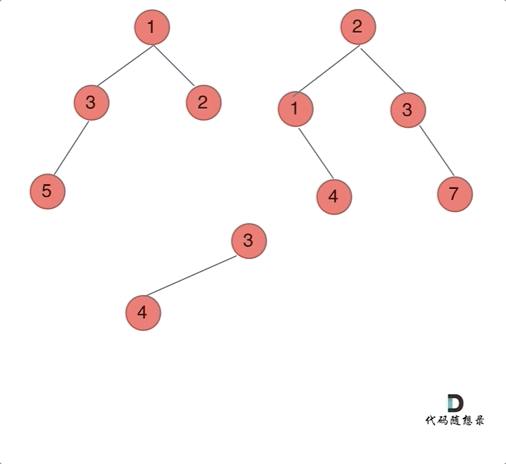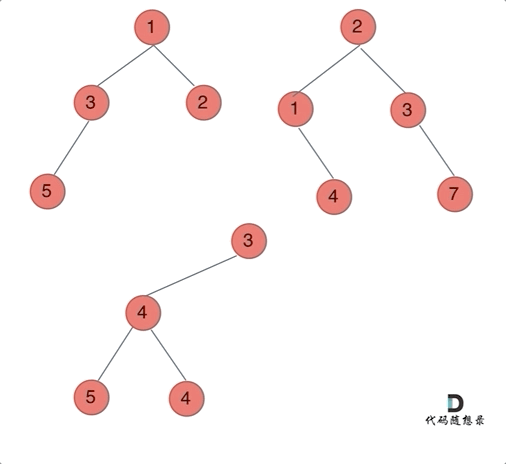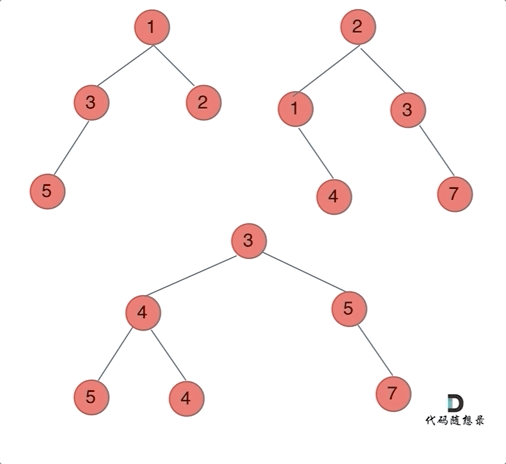
思路:以建立的节点为标准,类似于前缀【中后序】遍历进行构造!或者使用迭代法【建立两个队列进行维护就好了】
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
# 终止条件:但凡有一个节点为空,就返回另一个节点,如果另一个也为None就直接返回None
# 以创建的新节点为移动标准
if not root1:
return root2
if not root2:
return root1
node = TreeNode()
node.val = root1.val + root2.val
node.left = self.mergeTrees(root1.left, root2.left)
node.right = self.mergeTrees(root1.right, root2.right)
return node
def mergeTrees1(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
if not root1 and not root2:
return
node = TreeNode(0)
if root1 and root2:
node.val = root1.val + root2.val
node.left = self.mergeTrees(root1.left,root2.left)
node.right = self.mergeTrees(root1.right, root2.right)
elif root1 and not root2:
node.val = root1.val
node.left = self.mergeTrees(root1.left,None)
node.right = self.mergeTrees(root1.right,None)
else:
node.val = root2.val
node.left = self.mergeTrees(None,root2.left)
node.right = self.mergeTrees(None,root2.right)
return node
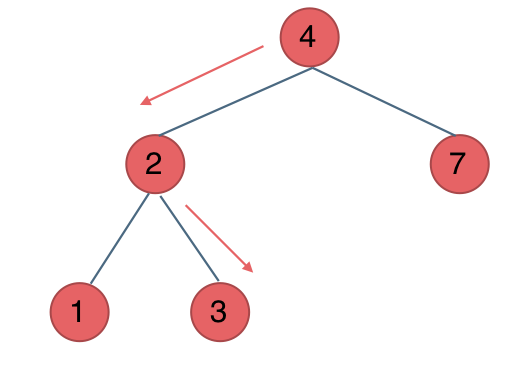
700. 二叉搜索树中的搜索
思想:使用层次遍历或者使用递归或迭代
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
# 层次遍历
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
queue_1 = []
if not root:
# return queue_1.append(root) 犯下了致命弱智的错误
return None
queue_1.append(root)
while len(queue_1) > 0:
node = queue_1.pop(0)
if node.val == val:
return node
if node.left:
queue_1.append(node.left)
if node.right:
queue_1.append(node.right)
return None
# 迭代法
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
while root:
if root.val > val:
root = root.left
elif root.val < val:
root = root.right
else:
return root
return None
# 递归法
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
# 为什么要有返回值:
# 因为搜索到目标节点就要立即return,
# 这样才是找到节点就返回(搜索某一条边),如果不加return,就是遍历整棵树了。
if not root or root.val == val:
return root
if root.val > val:
return self.searchBST(root.left, val)
if root.val < val:
return self.searchBST(root.right, val)
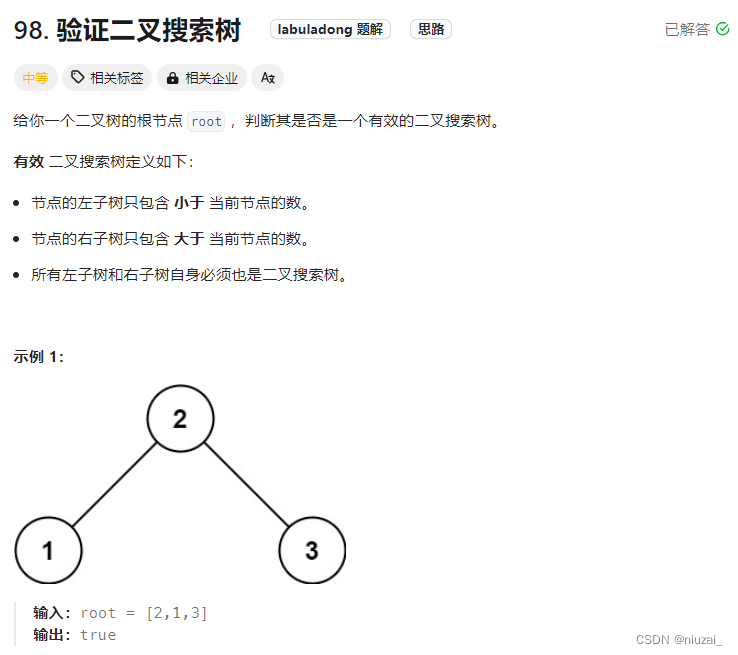
98. 验证二叉搜索树
核心:理解中序遍历的规则,在二叉树中中序遍历出来的结果一定是有序的!
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.nums = []
def isValidBST(self, root: Optional[TreeNode]) -> bool:
# 中序遍历出来的数一定是有序的
self.nums = [] # 清空数组
self.traversal(root)
for i in range(1, len(self.nums)):
# 注意要小于等于,搜索树里不能有相同元素
if self.nums[i] <= self.nums[i - 1]:
return False
return True
def traversal(self, root):
if root is None:
return
self.traversal(root.left)
self.nums.append(root.val) # 将二叉搜索树转换为有序数组
self.traversal(root.right)
# 设置最小值比较,就可以修改了单层逻辑那个地方,左了一个比较!
class Solution:
def __init__(self):
self.maxVal = float('-inf') # 因为后台测试数据中有int最小值
def isValidBST(self, root):
if root is None:
return True
left = self.isValidBST(root.left)
# 中序遍历,验证遍历的元素是不是从小到大
if self.maxVal < root.val:
self.maxVal = root.val
else:
return False
right = self.isValidBST(root.right)
return left and right
文章来源:https://blog.csdn.net/niuzai_/article/details/135072206
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!