007文章解读与程序——电力系统自动化EI\CSCD\北大核心《含冰蓄冷空调的冷热电联供型微网多时间尺度优化调度》已提供下载资源
👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆下载资源链接👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆
摘要:冷热电联供型微网(CCHP-MG)对实现能源可持续发展和构建绿色低碳社会具有重要的应用价值,而内部复杂的能源结构与设备耦合关系、可再生能源的消纳和负荷波动的平抑给其优化运行带来了挑战。文中提出含冰蓄冷空调的CCHP-MG多时间尺度优化调度模型,研究冰蓄冷空调的不同运行方式对优化调度的影响。日前计划中通过多场景描述可再生能源的不确定性,侧重于一个运行优化周期内CCHP-MG的经济运行;日内调度基于日前计划方案,根据冷热电在不同时间尺度上的相关性和互补性,提出考虑冷热负荷变化的双层滚动优化平抑模型,求解各联供设备的调整出力。仿真结果表明:冰蓄冷空调的运行方式关系到CCHP-MG的综合效益的提高;多时间尺度优化调度模型不仅可以满足用户的冷、热、电能的需求,还能有效平抑日内阶段供需侧随机性波动,实现CCHP-MG经济及稳定运行。行带来了挑战。文中提出含冰蓄冷空调的CCHP-MG多时间尺度优化调度模型,研究冰蓄冷空调的不同运行方式对优化调度的影响。日前计划中通过多场景描述可再生能源的不确定性,侧重于一个运行优化周期内CCHP-MG的经济运行;日内调度基于日前计划方案,根据冷热电在不同时间尺度上的相关性和互补性,提出考虑冷热负荷变化的双层滚动优化平抑模型,求解各联供设备的调整出力。仿真结果表明:冰蓄冷空调的运行方式关系到CCHP-MG的综合效益的提高;多时间尺度优化调度模型不仅可以满足用户的冷、热、电能的需求,还能有效平抑日内阶段供需侧随机性波动,实现CCHP-MG经济及稳定运行。?
部分代码展示:
clc
clear all
%%
%场景法
%%% wf1 wf2 为平均值
wf1=[339,287,449,471,512,530,527,641,634,519,401,634,589,530,512,505,206,85,81,80,83,110,353,523];
wf2=[0,0,0,0,0,0,99,137,150,178,189,191,176,171,138,104,77,0,0,0,0,0,0,0];
m1=ones(24,1000);%风生成
m2=ones(24,1000);%光生成
m=ones(24,1000);%可再生生成
%%
%生成1000个场景
%%
%拉丁差立方抽样方法
%%%拉丁超级方抽样=====属于分层抽样技术(从多元参数分布中近似随机抽样的方法)------分层抽样:将抽样区间(本程序为正态分布区间)
%按某种特性或某种规划分为不同的层,然后从不同的层中独立、随机(打乱排序,无规律抽取)
%地抽取样本(如取10个苹果样本,按照特性把苹果树分为5类,每类随机取2个),从而保证样本的结构与总体的结构比较相近,提高估计的精度。
%拉丁超立方相较蒙卡,改进了采样策略能够做到较小采样规模中获得较高的采样精度。
%%lhsnorm(mu,sigma,n); mu平均值(数量a); 求解公式:u=(1/N)*(sum(样本));N为样本数目
% sigma协方差矩阵(数量a*a); 求解公式: =((1/N)^3)*(sum(样本i-u)^2); i=1至N
% n抽样次数
% 表示方式1
% % c=1;%c 表示基础数据的数量
% % u1=lhsdesign(1,24);
% % u2=lhsdesign(1,24);
% % for t=1:24
% % m1(t,:)=lhsnorm(sum(wf1(:,t))/c,u1(t)*sum(wf1(:,t))/c,1000); %拉丁超立方抽样(lhsnorm函数)方法
% % (基于风电和光伏出力遵从正态分布normrnd(均值,标准差,n,m) n*m阶正态矩阵 ),
% % 因此lhsnorm函数的均值和标准差采用正态分布的均值,标准差
% % 依据文献,可以假定标准差与均值之间存在一定比例关系。
% % if t>=7&&t<=17
% % m2(t,:)=lhsnorm(sum(wf2(:,t))/c,u2(t)*sum(wf2(:,t))/c,1000);
% % else
% % m2(t,:)=0;
% % end
% % m(t,:)=m1(t,:)+m2(t,:);
% % end
%%
% 表示方式2
for t=1:24
m1(t,:)=normrnd(wf1(t),0.12*wf1(t),1,1000); %正态分布 normrnd(均值,标准差,n,m) n*m阶正态矩阵
m2(t,:)=normrnd(wf2(t),0.1*wf2(t),1,1000);
m(t,:)=m1(t,:)+m2(t,:);
end
%% 场景生成图
figure()
plot(m1,'--')
hold on
plot(m2,'-')
hold on
l2=xlabel('t/h');
set(l2,'Fontname', 'Times New Roman','FontSize',20)
l3=ylabel('P/kW');
set(l3,'Fontname', 'Times New Roman','FontSize',20)
set(gca,'FontName','Times New Roman','FontSize',20)
%%
%场景削减(快速后向削减)
%原理:确定初始场景集合的一个子集,并给其重新分配场景概率,使保留场景的概率分布Q与初始场景集合的概率P之间的某种概率距离最短(即,P与Q相近),
%从而削减概率小的概率,将其加到与其场景的概率距离最近的场景上。
%%
%计算各个场景之间的概率距离
k=zeros(1000,1000);
for i=1:1000
for j=1:1000
if i==j
k(i,j)=0;%K距离
else
k(i,j)=sqrt(sum((m(:,i)-m(:,j)).^2));
end
end
end
p=ones(1000,1)*0.001;%各场景初始概率
%%
%%寻找最小概率距离场景
k1=k;b2=[];k1(k1==0)=inf;
for n=1:990%削减990次,保留10个概率最高场景
[mink,index]=min(k1,[],2);%index每行最小坐标列 %mink 每行最小数值 % min(k1,[],2) 求取每行的最小值; min(k1,[],1)求取每列的最小值
%%
%删去index2 行 %%min(mink.*p) 概率最低。。。被淘汰
[mink11,index2]=min(mink.*p);
b=index2;
%减少一个场景
k1(b,:)=[];
k1(:,b)=[];
%%
b2=[b2;b];
%%
%新概率生成
a=index(index2);%与被削减场景的概率距离最近的场景a
%新场景概率a=原来对应场景概率a+概率重新分配系数*与此情景概率距离最近场景index2
p(a)=p(index2)+p(a);效果图展示:
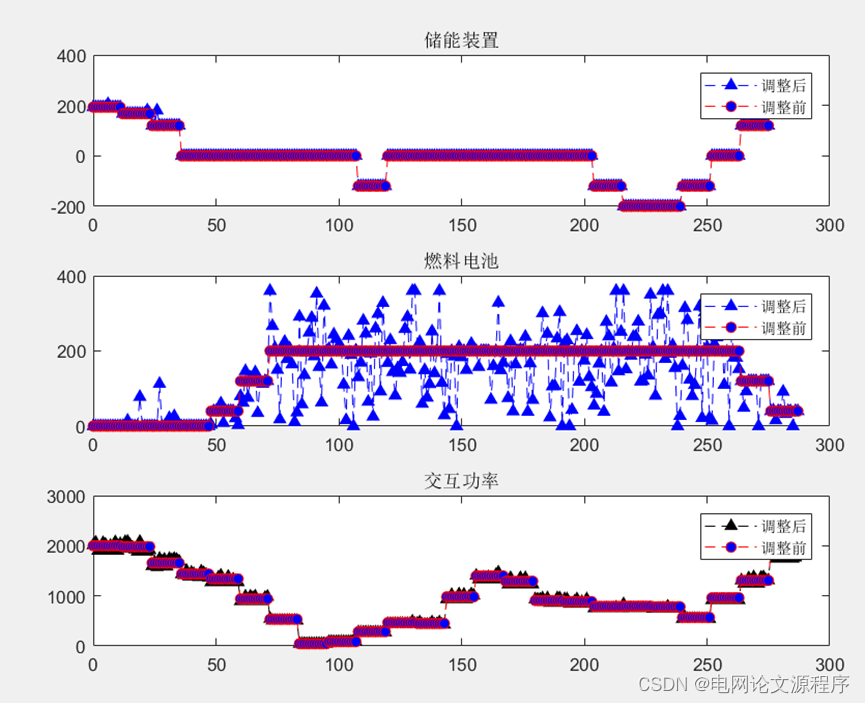
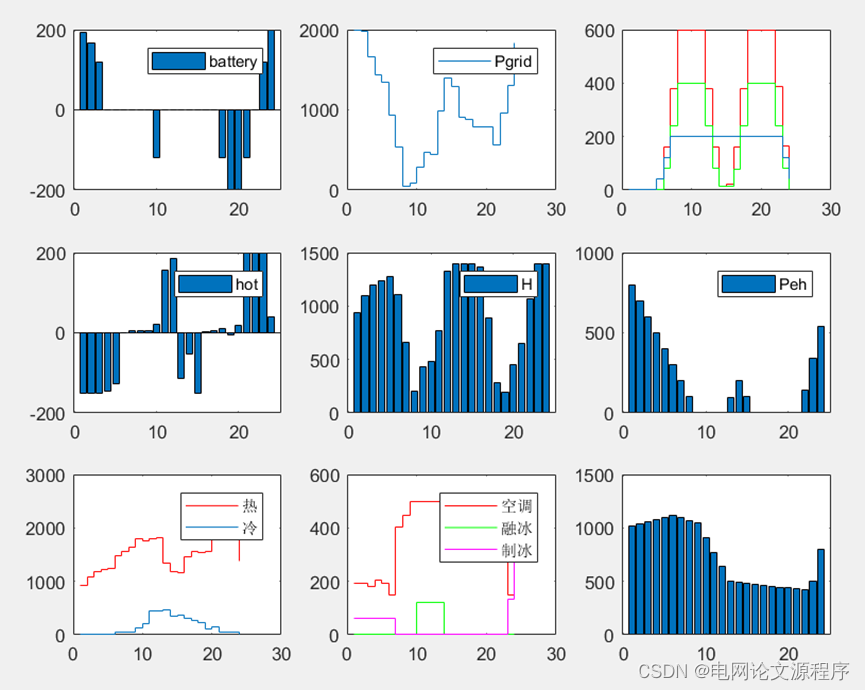
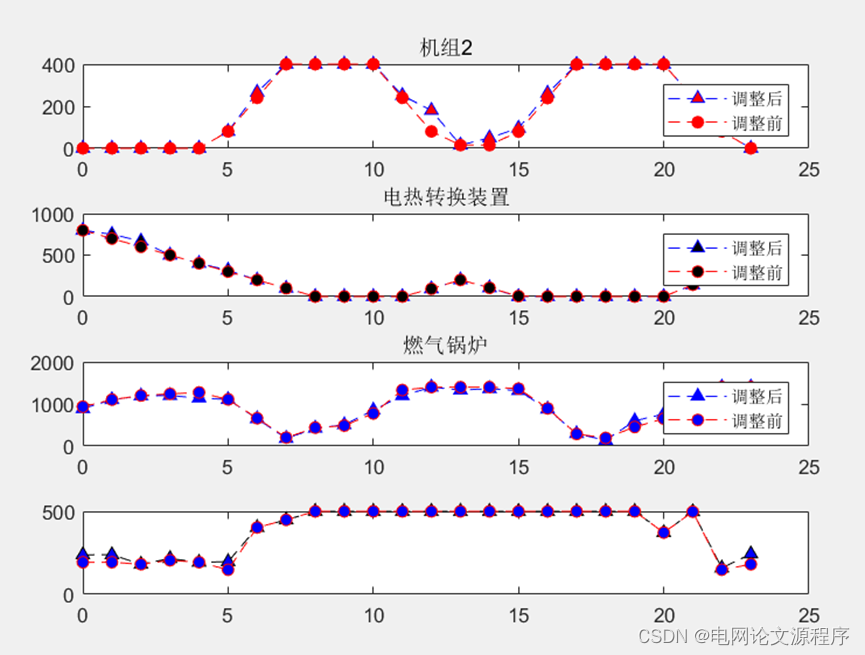
资源链接![]() https://download.csdn.net/download/LIANG674027206/88689355???????
https://download.csdn.net/download/LIANG674027206/88689355???????
👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆下载资源链接👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!