(2023|AABI,多模态信息瓶颈,变分近似,视觉语言模型可解释性)通过多模态信息瓶颈归因对图像文本表示的视觉解释
Visual Explanations of Image-Text Representations via Multi-Modal Information Bottleneck Attribution
公和众和号:EDPJ(添加 VX:CV_EDPJ 或直接进 Q 交流群:922230617 获取资料)
目录
0. 摘要
视觉语言预训练模型取得了显著的成功,但它们在安全关键环境中的应用受到了可解释性的限制。为了提高诸如 CLIP 之类的视觉语言模型的可解释性,我们提出了一种多模态信息瓶颈(multi-modal information bottleneck,M2IB)方法,该方法学习潜在表示,压缩无关信息同时保留相关的视觉和文本特征。我们演示了 M2IB 如何应用于视觉语言预训练模型的归因分析,提高了归因的准确性,并在应用于诸如医疗保健等安全关键领域时改善了这些模型的可解释性。至关重要的是,与通常使用的单模态归因方法不同,M2IB 不需要地面真实标签,这使得在存在多模态但没有地面真实数据的情况下审计视觉语言预训练模型的表示成为可能。以 CLIP 为例,我们展示了 M2IB 归因的有效性,并且在定性和定量上显示它优于基于梯度、基于扰动和基于注意力的归因方法。
我们实验的代码位于:https://github.com/YingWANGG/M2IB。
3. 通过多模态信息瓶颈原理进行归因
在这一部分,我们介绍了信息瓶颈(information bottleneck)原理的一个简单、多模态变体,并解释了如何将其调整为特征归因。
3.1 信息瓶颈原理
信息瓶颈原理 [32] 提供了一个框架,用于找到神经网络模型的压缩表示。为了获得反映输入数据最相关信息的潜在表示,信息瓶颈原理试图找到由参数编码器
![]()
定义的输入源 X 的随机潜在表示Z,该表示在约束潜在表示 Z 和输入 X 之间的互信息的同时,对目标 Y 具有最大信息量。对于由参数 θ 参数化的表示,该原理可以表达为优化问题:
![]()
其中 I(·, ·; θ) 是互信息函数,而 ˉI 是一个压缩约束。我们可以等价地表达这个优化问题,即最大化目标:
![]()
其中 β 是一个拉格朗日乘子,用于权衡学习一个关于目标 Y 最具信息的潜在表示和学习一个关于输入 X 最大压缩的表示 [2]。
3.2 多模态信息瓶颈原理
不幸的是,对于 VLPMs,上述的损失函数不适用,因为我们希望使用仅依赖于文本和视觉输入来学习可解释的潜在表示,而不依赖于可能不可用或昂贵获取的任务特定目标 Y。为了为 VLPMs 制定一个多模态信息瓶颈原理,我们需要开发一个更类似于仅使用(文本,图像)对的图像文本表示学习的自监督方法的优化目标 [21, 18]。
这个学习问题在本质上与单模态任务的监督归因图学习不同。例如,我们可能有一张熊的图片X_bear 和一个相应的标签 Y_bear = “bear”。对于单模态分类任务,我们可以简单地相对于 θ 最大化 I(Y_bear; Z_bear; θ) ? β·I(X_bear; Z_bear; θ),其中 Z_bear 是 X_bear 的潜在表示。
相比之下,在图像文本表示学习中,我们通常有文本描述,比如 “这是一张熊的图片”(L′_bear),而不是标签 [21]。在这种情况下,X_bear 和 L′_bear 都是 “输入”,没有预定义的相应标签。为了获得与任何任务特定的真实标签无关的任务不可知(task-agnostic)的图像文本表示,我们希望使用两个输入模态来定义一个多模态信息瓶颈原理,而输出则与具体的下游任务密切相关。这需要定义一个替代传统信息瓶颈目标的 “拟合项” I(Z, Y; θ)。
幸运的是,在多模态数据中,有一个自然的信息相关性代理。如果图像和文本输入(例如,描述图像的文本)相关,良好的图像编码应该包含关于文本的信息,反之亦然。基于这一直觉,我们可以表达一个对于 m ∈M= {modality1, modality2} 的 X_m 的多模态信息瓶颈目标,如下所示:
![]()
其中 m′ = M\m 是 m 的补集,而 E_m′ 是模态 m′ 的嵌入(注:基于公式 6 和 7,这里下标应为 m')。接下来,我们将展示如何使用这个多模态信息瓶颈原理的变体进行归因。
3.3 用于归因的多模态信息瓶颈
为了在没有访问任务特定标签的情况下计算图像和文本数据的归因图,我们将为多模态数据定义一个信息瓶颈归因方法。
为了通过一个简单的参数编码器限制潜在表示中的信息流,我们采用了 Schulz 等人的掩蔽方法 [24]。为了清晰和简洁起见,我们从现在开始以 RJ 表示 V_m × W_m 维的潜在表示 Z_m,其中
![]()
假设在潜在表示维度上独立,我们然后定义
![]()
其中,对于模态对 M= {image, text} 中的每个 m ∈ M,θm = {λm, σm, ?m} 是参数,hm(xm; λm) ∈ R^J 是由 λm 参数化的映射,f^?_m(Xm) ∈ R^J 是模态特定神经网络嵌入 fm 的第 ?m 层的矢量化输出,σ^2_m ∈ R > 0 是一个超参数,diag[·] 表示一个操作符,通过将向量的元素沿主对角线放置,将向量转换为对角矩阵,1_J ∈ R^J 是一个全 1 矢量, ⊙ 是 Hadamard 积。为避免符号过载,除非需要明确表示,否则我们将省略概率密度函数中的下标。基于方程(4),我们可以表达随机潜在表示为:
![]()
其中,ε ~ N(0, I_J )。通过这个重参数化,我们可以看到 [hm(xm; λm)]_i = 1 对于 i ∈ {1, ..., J} 意味着在索引 i 处没有添加噪声,因此 [Zm]_i 将与原始的 f^?_m(xm)_i 相同,而 [hm(xm; λm)]_i = 0 意味着 [Zm]_i 将是纯噪声(i 表示对角阵的索引。简单的线性组合)。
现在我们可以表达多模态信息瓶颈归因(M2IB)目标,如下所示:

我们可以分别针对模态特定的参数集 λ_image 和 λ_text 进行优化。{β_image, σ_image, ?_image} 和 {β_text, σ_text, ?_text} 分别是超参数集。
3.4 用于多模态信息瓶颈归因的变分目标
为了得到可行的优化目标,我们使用了一个变分近似。首先,我们注意到
![]()
其中 Zm | Xm; θm 可以通过经验抽样,而 p(zm; θm) 没有解析表达式,因为积分
![]()
是不可计算的。为了解决这个不可计算性,我们通过
![]()
近似 p(zm)。这个近似导致了上界:
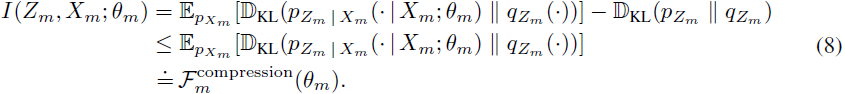
接下来,尽管单模态信息瓶颈归因目标使用真实标签来计算目标中的 “拟合项”,但多模态信息瓶颈归因目标需要计算对齐随机嵌入之间的互信息,

这在一般情况下是不可计算的。为了获得解析可计算的变分目标,我们通过一个变分分布 q(em′ | zm) = N(em′ ; gm(zm), I_K) 来近似不可计算的 p(em′ | zm),其中 gm 是一个将模态 m 的潜在表示与 Em′ 对齐的映射,K 是嵌入的维度,得到(链式法则):
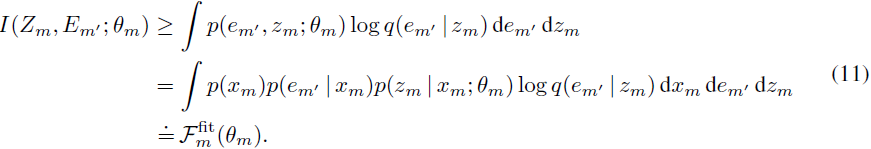
有了这个近似,我们可以通过从经验分布(公式 12)中抽样 Xm 和 Em' 来获得一个可行的变分优化目标。

其中 fm′?(xm′?) 是 VLPM 下输入 xm′? 的嵌入。通过这些近似,我们现在可以陈述完整的变分目标,如下所示:
![]()
这个目标的推导紧密地遵循了 [2] 中的步骤。在实践中,可以使用经验数据分布来计算这个目标,以便
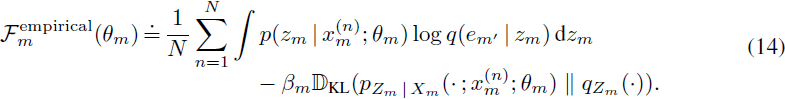
注:第一项组合了公式 12 的冲激函数和公式 11。?
最终变分优化目标。最后,我们假设 hm?(xm(n)?;λm?)=λm(n)?(即,每个输入点都有自己的归因参数集),gm? 是由 VLPM 的瓶颈后层定义的映射,并且对于每个评估点,每个模态的最终嵌入在嵌入维度上进行归一化(即,映射 gm? 和 fm′? 都包含嵌入归一化变换)。对于归一化的 gm?(zm?) 和?em′?,Gaussian 概率密度 q(fm′?(xm′?)∣gm?(zm?)) 的对数简化为正比于 fm′?(xm′?) 和 gm?(zm?) 之间的余弦相似性,给出最终的优化目标:
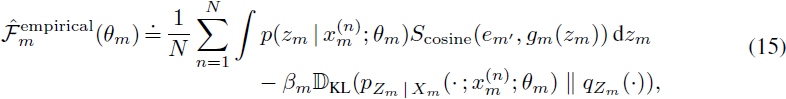
其中 S_cosine?(?,?) 是余弦相似性函数。在优化过程中进行梯度估计时,可以使用简单的蒙特卡洛估计和重参数化梯度来估计剩余的积分。对于 θm?={λm?,σm?,?m?},目标函数独立地针对每个模态的 λm? 进行最大化,而 βm?, σm? 和 ?m? 是模态特定的超参数。?
4. 评估
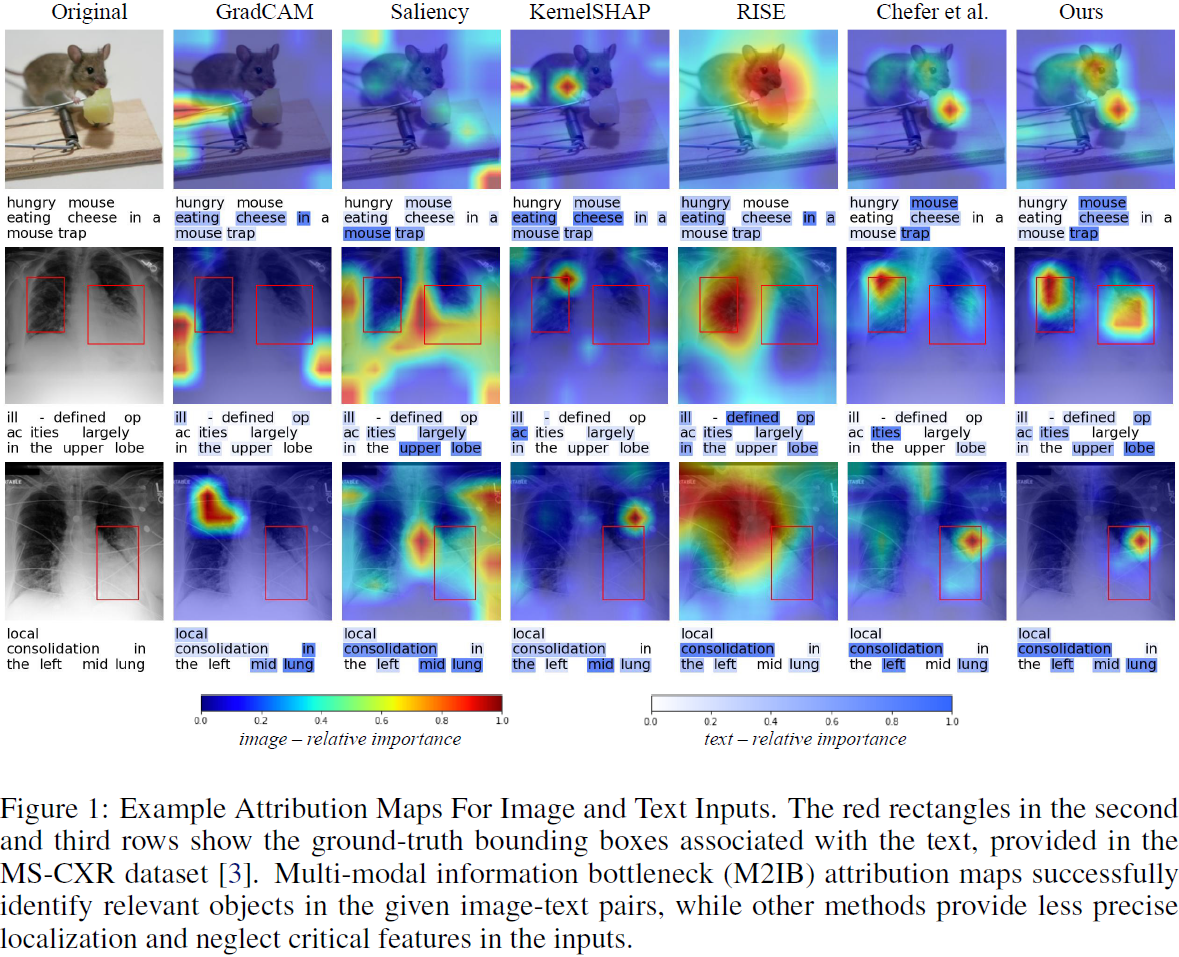

对不同目标的归因图。?
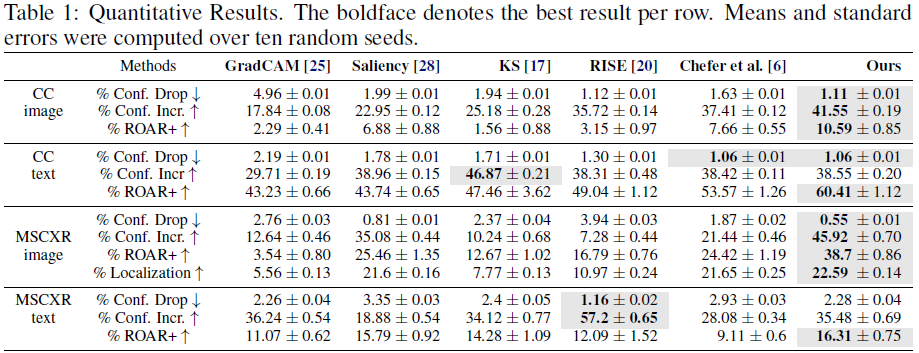
置信度下降(Drop in Confidence) [4]。理想的归因方法应该只给重要特征分配高分,因此,如果只允许输入高归因部分,我们不应该观察到性能下降。?
置信度提高(Increase in Confidence) [4]。类似地,去除输入中的噪声信息可能会增加模型的置信度。
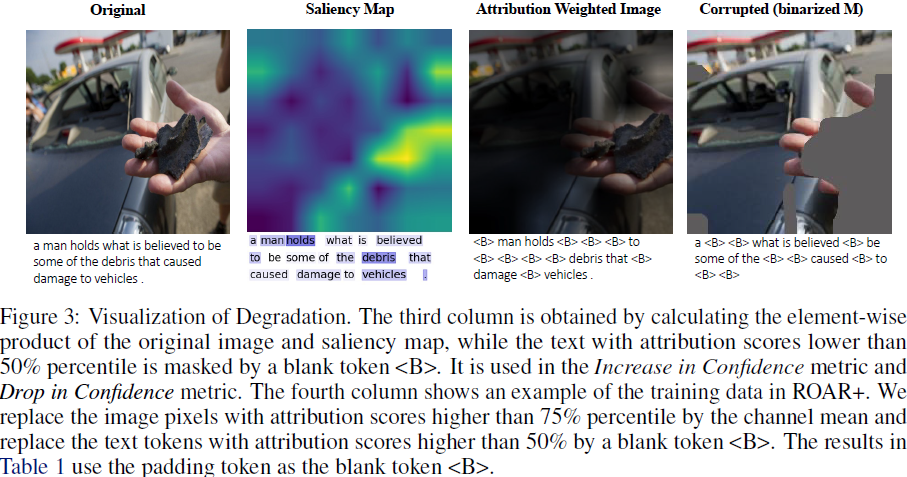
删除和重新训练 +(Remove and Retrain +,ROAR+,ROAR [11] 的扩展)。我们在退化的图像和文本上微调基础模型,其中最重要的部分被替换为不相关的值(即,图像的通道均值或文本的填充标记,参见图 3),并在原始输入的验证集上进行评估。如果归因方法准确,我们期望性能会急剧下降,因为所有有用的特征都被移除,而模型无法从退化的数据中学到任何相关的信息。
4.6 错误分析与局限性
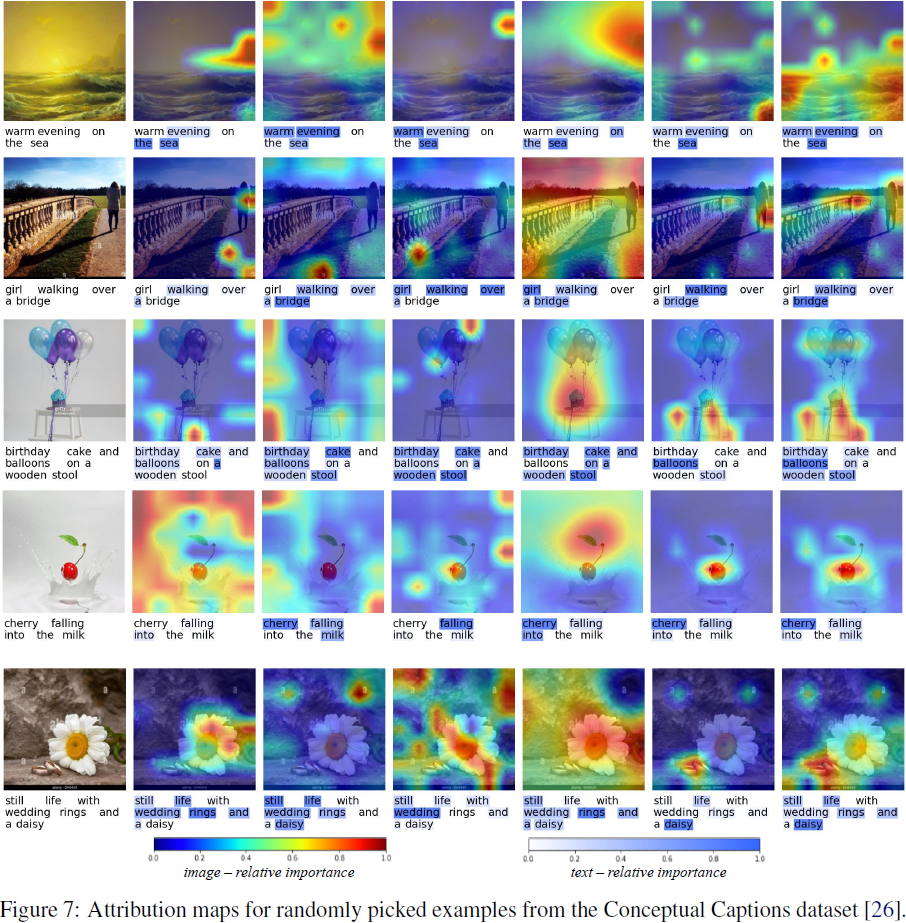
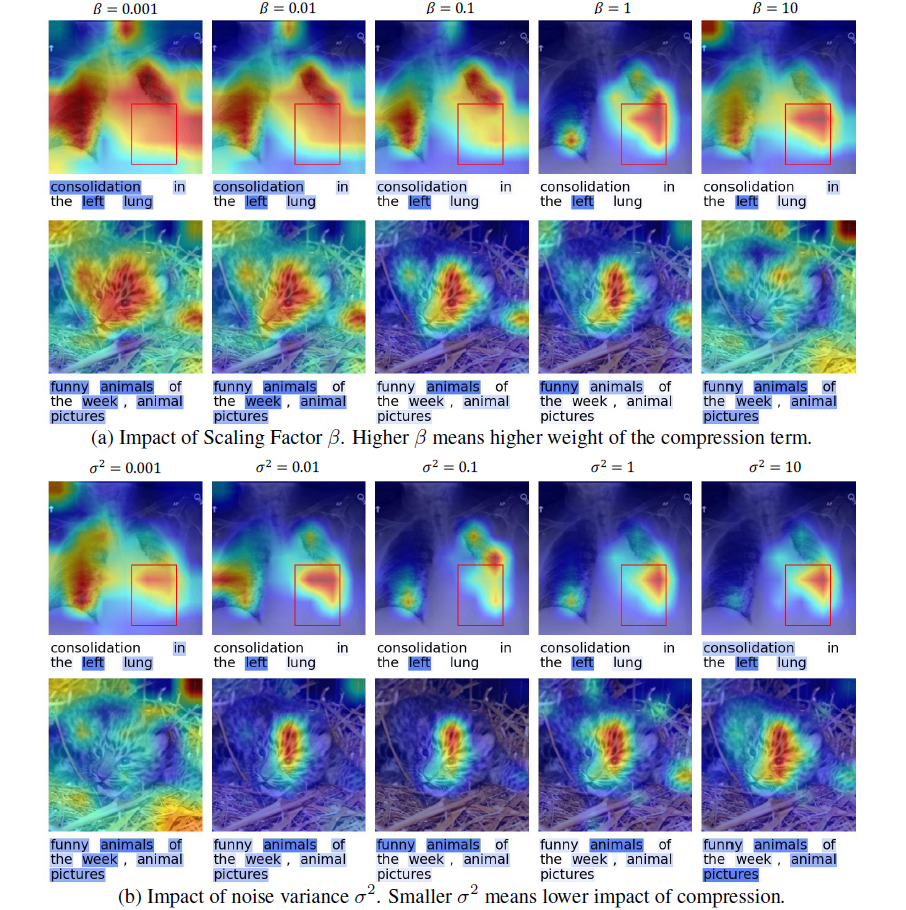
我们注意到我们提出的归因方法在文本上表现普遍良好,但有时在图像上表现不太令人满意。通过检查定性示例,我们观察到 M2IB 有时无法检测到图像中的整个相关区域。如图 7 的 “sea” 示例和 “bridge” 示例所示,我们的方法只突出显示图像中的一部分对象,尽管应该包括整个对象。这可能是因为评估中的模型仅依赖图像中的一些模式来进行预测。增加拟合项的相对重要性(即,使用较小的 β)会扩大突出显示的区域。然而,我们不建议使用极端的 β,因为这会破坏拟合和压缩之间的平衡,从而使信息瓶颈无法压缩信息。
我们还注意到 M2IB 对超参数的选择敏感。如图 5 所示,不同的超参数组合将生成不同的显著性图。我们展示了如何使用 ROAR+ 分数系统地选择最佳超参数,并在附录 A 中提供可视化,以说明不同超参数的效果。由于在评估归因方法方面没有公约,我们建议在选择超参数时考虑各种评估指标、示例的可视化以及归因任务的目标。我们强调 M2IB 应谨慎使用,因为将模型的成功或失败仅归因于一组特征可能过于简单,而不同的归因方法可能导致不同的结果。?

S. 总结
S.1 主要贡献
为了提高诸如 CLIP 之类的视觉语言模型的可解释性,本文提出了一种多模态信息瓶颈(multi-modal information bottleneck,M2IB)方法,该方法学习潜在表示,压缩无关信息同时保留相关的视觉和文本特征。与通常使用的单模态归因方法不同,M2IB 不需要地面真实标签,这使得在存在多模态但没有地面真实标签的情况下审计视觉语言预训练模型的表示成为可能。
S.2 方法
多模态信息瓶颈:仅依赖文本标题和视觉输入来学习可解释的潜在表示,而不依赖可能不可用或昂贵获取的任务特定目标标签?Y。
在多模态数据中,如果图像和文本输入(例如,标题)相关,良好的图像编码应该包含关于文本的信息。基于此,多模态信息瓶颈归因(M2IB)最大化如下目标:

其中,Z 是潜在表示,?E 是模态(图像/标题)嵌入,X 是输入(图像/标题)。该公式通过变分近似进行优化。直观而言,该方法可提升图文对齐。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!