Numpy教程（一）—— ndarray：多维数组对象

前言

该numpy学习笔记参考了菜鸟教程网、b站up主 孙兴华zz 的《孙兴华中文讲python数据分析三部曲》以及《北理-python数据分析与展示》，课本推荐使用《利用python进行数据分析》

• Numpy简介：

? ? ? ? NumPy(Numerical Python) 是 Python 语言的一个扩展程序库，支持大量的维度数组与矩阵? ? ? ? ? ? 运算，此外也针对数组运算提供大量的数学函数库。

1.数组(array)的介绍

? ? ? ?数组是相同数据类型的集合，多个变量共用一个变量名称，并用下标加以区分

• 数组和列表

? ? ? ?数组和列表都是表达一组数据的有序结构的数据类型，但列表中的数据类型可以不同，数组中的数据类型必须相同

• 数组和矩阵

? ? ? ? 矩阵（matrix）是数组（array）的一个分支，很多时候二者是通用的，但建议选择数组，更灵活。一般，二维的array也翻译成矩阵?

• N维数组对象：ndarray?

? ? ? ndarray是一个多维数组对象，由两部分构成：实际的数据以及描述这些数据的元数据（如：维度、类型），

? ? ? ndarray数组一般要求所有元素类型相同（因为一般同一维度中，数据类型基本相同，便于计算），数组下标从0开始

? ? ? 优点：可以省去循环，使一维向量更像单个数据；底层实现通过c语言完成，提升计算速度

# 两种数组相加方式对比

# 利用for循环和列表相加两个数组
def shuzujiafa1(n):
    a = [i**3 for i in range(1,n+1)]
    b = [i**2 for i in range(1,n+1)]
    c = []
    for i in range(n):
        c.append(a[i]+b[i])
    return c
print(shuzujiafa1(3))

# 利用numpy库相加两个数组
import numpy as np
def shuzujiafa2(n):
    a = np.arange(1,n+1) ** 3
    b = np.arange(1,n+1) ** 2
    return a+b
print(shuzujiafa2(3))

2.ndarray对象的属性

属性	说明
n.ndim	返回ndarray对象的秩，即轴的数量或维度
n.shape	返回一个元组，表ndarray对象的形状 （几行几列）
n.size	返回ndarray对象中元素的个数
n.dtype	返回ndarray对象中所有元素的数据类型
n.itemsize	返回ndarray对象中每个元素的大小，以字节为单位

3.数组的创建方式

numpy每一次生成的数组中都要把元素作为浮点数（除了arrange函数），因为在科学计算中会大量用到浮点数?

?3.1 常规创建（从列表、元组等类型创建）

? 语法：np.array（ 列表 或 元组 或 数组等 ，dtype = xxx）? ?

? ? ? ? ? ? 其中列表可以用 range（a，b）代替，dtype是设置数组内对象的数据类型，默认自动识别

? ? ? ? ? ?

??

?3.2 使用函数创建特定数组

• ?常规函数?

函数	说明
np.ones（shape）	根据shape生成一个全1数组,shape是元组或整数类型 例：np.ones（(2,3)）一>? 生成两行三列的全为1的元组
np.zeros（shape）	根据shape生成一个全0数组,shape是元组或整数类型（同上）
np.full ( shape,value )	根据shape生成一个数组，每个元素值都是value
np.eye(n)	创建一个正方的n*n单位矩阵，对角线为1，其余为0
np.empty（shape）	根据shape生成一个空数组(一般用于初始化)

• like类函数：根据已有数组创建新数组

函数	说明
np.ones_like(a)	相当于把shape换成了数组a，根据数组a的形状生成想要的数组 即：数组a的shape就是新数组的shape
np.zeros_like(a)
np.empty_like(a)
np.full_like(a,value)
np.concatenate（(a，b)）	将两个或多个维数相同数组合并成一个新的数组

• 根据数值范围创建数组

函数	说明
np.linspace（start，stop，想要的元素个数，endpoint）	根据起止数据等间距的填充数据，形成数组 endpoint：bool类，最后一个元素是否要包含在数组中 例：np.linspace（1，10，4）一>? 数组：1，4，7，10
np.arange （[start,]? 结束? [,step]）	类似 array 和 range 函数的组合 例：np.arange(n)? 一>? 返回ndarray类型，元素从0到n-1

• 利用random函数生成随机数组

? ? ? ? ?语法：import random

? ? ? ? ? ? ? ? ? ? np.random.randn(shape)? ? ?生成shape型的随机数

? ? ? ? ?额外操作：保留小数位数

? ? ? ? ? ? ? ? ? ? np.round(a,2)?? #变量a，保留两位小数点

?3.3 高维数组的创建

• 方式一：序列（列表）的嵌套，如下：

a = np.array([[1,2],[3,4]])
b = np.array([[[1,2],[5,6]],
              [[1,2],[3,4]],
              [[1,2], [3,4]]])
print(a.ndim,b.ndim)  # 2 3
print(a.shape,b.shape) # (2, 2) (3, 2, 2)

a中数据是一个包含列表的列表，即双层嵌套，故形成了一个2*2的二维数组

b中数据是一个三层列表的嵌套，故形成了一个 3*2*2 的三维数组（可理解成三个2*2的二维数组）

• 判断高维列表维数的技巧：1）看array与第一个数字间有几个“ [ ”，就是几维

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? 2）看shape中有几个数就是几维? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??

• ?方式二：利用函数创建，为shape传递一个元组

c = np.zeros((3,2,1))
print(c)
print(c.ndim,c.shape) # 3 (3, 2, 1)

4.数组的变换

?4.1 维度的变换

方法	说明
arr.reshape（shape）	不改变数组元素，新建一个shape形状的数组，原数组不变 ? ? 要求：shape中乘积为元素总个数
arr.resize（shape）	同上，但修改原数组
arr.swapaxes（a，b）	将数组n个维度中两个维度进行调换
arr.flatten（）	对数组进行降维，返回折叠后的一维数组，原数组不变

?4.2 元素类型的变换

? ? ? ? ? ?语法：arr.astype（元素数据类型）

? ? ? ? ? ?说明：将数组中元素的类型进行转变，这个操作会新建一个数组，原数组不变

?4.3 数组转化为列表?

? ? ? ? ? ? ?语法：arr.tolist（）

? ? ? ? ? ? ?作用：数组中的计算速度更快，占用空间更小；但列表可以存储多种数据类型

import numpy as np
# 维度的变换
a = np.array([[1,2],[1,3],[1,2],[2,3]])
print(a)
print(a.ndim) # dim a = 2
print(a.shape)  # shape a = (4,2)

b = a.reshape((2,4))  # shape b = (2,4)
print(b)
print(b.ndim)   # dim b = 2
print("-" * 30)

# 元素类型的变换
c = np.ones((2,3,4),dtype = np.int32)
print(c)

d = c.astype(np.float32)
print(d)
print("-" * 30)

# 转化为列表
e = a.tolist()
print(e)
print(type(e))

5.数组计算

运算	说明	备注
a + 1	数组a的所有元素都加1 相当于加一个与a形状一样且全为1的数组	减乘除 同理
a + b a、b的shape一样	对应元素分别相加
a + b a是一维数组 b是多维数组	a的这一行，与b的每一行分别相运算	一维数组和多维数组可以运算 要求：在某一维度上shape一样

上述第三种运算，不同尺寸数组之间什么时候可以运算？—— 广播原则

• 广播原则

??如果两个数组的后缘维度（即从末尾开始算起的维度）的轴长度相符，或其中的一方的长度为1，则认为它们是广播兼容的。广播会在缺失的 或长度为1的维度上进行。

?例如：（3，2，3）和（2，3）：可以运算，后缘维度都是（3，2）

? ? ? ? ? ? （3，2，2）和（2，1）：可以运算，后者后缘维度长度是1

? ? ? ? ? ? （3，2，4）和（1，4）：可以运算，最后一个后缘维度相等，倒数第二个后者为1

? ? ? ? ? ? （3，2，4）和（1，2）：不能运算，后缘维度不相等，且均不为1

6.数组的索引和切片

?6.1 基础索引

• 一维数组的索引和切片（与python列表类似）

? ? ? ?编号方式：从0开始向右递增；或者从-1开始向左递减

? ? ? ?索引：数组名 [ 编号数 ]

? ? ? ?切片：数组名 [ 起始编号：终止编号（不含）：步长?]

• 多维数组的索引和切片（以三维数组为例）

? ? ? ? 索引：数组名 [ a , b , c?]? ? 每个维度一个索引值，用逗号分割

? ? ? ? 切片：同上，在每个维度上分别切片（方法同一维），中间用逗号隔开

? ? ? ? ? ? ? ? ? ?切片本质上是分别在在轴上进行切片

特殊形式：[ : , 1:3 , ::2?]? ?

?“ ：” 表示在这个维度上全部都取

?“1：3” 表示在这个维度上取编号1~编号3的元素

? “ ：：2 ” 表示在这个维度上从头取到尾，步长为2

??

• 注：由于Numpy经常处理大数组，避免每次都复制，所以切片在修改时直接修改了原数组?

import numpy as np
a = np.array(range(12)).reshape(3,2,2)
print(a)
b = a[2:,1:,:] 
print(b)
a[2:,1:,:] = 50 # 修改a中切片的值
print(a) # a数组也跟着发生变化

? ? ? ??我们也可以利用这一点来修改数组的数据，例如：

import numpy as np
arr = np.zeros((4,3),dtype=int)
arr[:] = 5 #相当于切片了所有数据
print(arr)

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

?6.2 布尔索引?

与数学操作类似，数组的比较操作也是可以向量化的，因此比较数组会返回给我们一个bool值数组

直接输入print（条件）即可，也可利用 数组名[ 条件?] = n 来进行赋值

• 例1：把一维数组进行01化处理（大于5的设为1，小于5的设为0）

import numpy as np
a = np.arange(13)
print(a)
a[a <= 5] = 0
a[a > 5] = 1
print(a) #结果为：[0 0 0 0 0 0 1 1 1 1 1 1 1]

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

• 例2：找出大于6且为偶数的数，并赋值为0

? ? ? ? python的关键字and 和 or 对布尔数值并没有用，需要使用 & 和 | 来代替

? ? ? ? 另外，~ 符号可以用来对一个条件取反时使用

import numpy as np
a = np.arange(12).reshape(2,6)
print(a)
print("-"*40)
tiaojian = (a%2==0) & (a>5) #条件
print(tiaojian)
a[tiaojian] = 0
print("-"*40)
print(a)

?6.3 神奇索引

神奇索引主要用于描述使用整数数组进行数据索引

import numpy as np
a = np.arange(32).reshape(8,4)
print(a)
print("-"* 30)
print(a[[4,3,0,6]])   # 返回第4行，第3行，第0行，第6行
print("-"* 30)
print(a[[1,5,7,2],[0,3,1,2]])   # 取第1行第0列，第5行第3列，第7行第1列，第2行第2列

• 案例：获取数组中最大的前N个数字

import numpy as np
a = np.random.randint(1,100,10)
print(a)
xiabiao = a.argsort()[-3:] #argsort()会返回排序后的下标，选取最大的三个
print(xiabiao)
max = a[xiabiao]
print(max)

? ? ? ? ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

7.数组的轴（axis）

?7.1 轴的介绍

? ? ?在官网中有这样一句话：“?In NumPy dimensions are called axes”，即维度称为轴?

? ? 一般如果维度是二维，我们就可以用x、y轴去描述一个点；如果是三维，就需要再加上z轴

? ? 所以我们可以将二者等价理解? ? ? ? ? ??

• 凡是提到轴，先看数组的维度，有几维就有几个轴? ? ? ?

? ? ??轴的编号 和 切片时我们使用的shape元组的索引是对等的，一条轴其实就是一个维度（层级）

? ? ? 而且轴的方向与索引编号方向一致

? ? ? 例如：shape（3，2，4）：分别对应（0轴，1轴，2轴）；

? ? ? ? ? ? ? ? ? ?而对具体维度而言，0轴对应三维，1轴对应二维，2轴对应一维

• 我们经常用到的shape可以理解为在每个轴（axis）上的size

? ? ? ?如下图：axis=0表示第一层(黑色)，该层数组的size为3；axis=1表示第二层(红色)，该层数组的size为2；axis=2表示第三层(蓝色)，对应轴上的元素length = 4。

?

?7.2 numpy转置换轴

? 例：要将data（2，3）转化为（3，2）

?

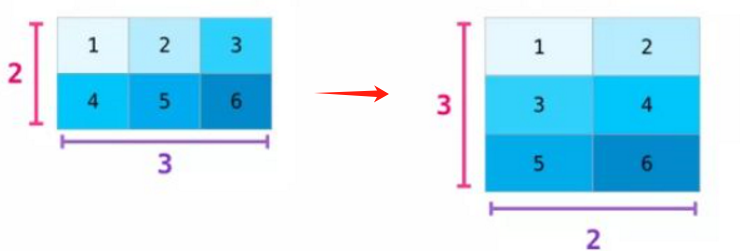方法	语法	说明
reshape（重组）	data.reshape（3，2）
transpose（矩阵转置）	data.transpose ( ) 也可简写为? data.T	行列转置
swapaxes（轴转置）	data.swapaxes(1,0)	该方法参数接收一对轴编号， 并对轴进行调整用于重组数据

? ? ?