第5章 散列
????????我们在第4章讨论了查找树ADT,它允许对一组元素进行各种操作。本章讨论散列表(hash?table)ADT,不过它只支持二叉查找树所允许的一部分操作。
????????散列表的实现常常叫作散列(hashing)。散列是一种以常数平均时间执行插入、删除和查找的技术。但是,那些需要元素间任何排序信息的操作将不会得到有效的支持。因此,诸如FindMin、FindMax以及以线性时间将排过序的整个表进行打印的操作都是散列所不支持的。
????????这章的中心数据结构是散列表,我们将:
- 看到实现散列表的几种方法。
- 分析比较这些方法。
- 介绍散列的多种应用。
- 将散列表和二叉查找树进行比较。
5.1 一般想法
????????理想的散列表数据结构只不过是一个含有关键字的具有固定大小的数组。典型情况下,一个关键字就是一个带有相关值(例如工资信息)的字符串。我们把表的大小记作TableSize,并将其理解为散列数据结构的一部分而不仅仅是浮动于全局的某个变量。通常的习惯是让表从0到TableSize-1变化,稍后我们就会明白为什么要这样。
????????将每个关键字映射到从0到TableSize-1这个范围中的某个数,并且放到适当的单元中。这个映射就叫作散列函数(hash?function),理想情况下它应该运算简单并且应该保证任何两个不同的关键字映射到不同的单元。不过,这是不可能的,因为单元的数目是有限的,而关键字实际上是无穷无尽的。因此,我们寻找一个散列函数,该函数要在单元之间均匀地分配关键字。图5-1是一个典型的理想情况。在这个例子中,john散列到3,phil散列到4,dave散列到6,mary散列到7。
这就是散列的基本想法。剩下的问题则是要选择一个函数,决定当两个关键字散列到同一个值的时候(称为冲突(collision))应该做什么以及如何确定散列表的大小。

5.2 散列函数
????????如果输入的关键字是整数,则一般合理的方法就是直接返回“Key?mod?TableSize”的结果,除非Key碰巧具有某些不理想的性质。在这种情况下,散列函数的选择需要仔细考虑。例如,若表的大小是10而关键字都以0为个位,则此时上述标准的散列函数就是一个不好的选择。其原因我们将在后面看到,而为了避免上面那样的情况,好的办法通常是保证表的大小是素数。当输入的关键字是随机整数时,散列函数不仅算起来简单而且关键字的分配也很均匀。
????????通常,关键字是字符串;在这种情形下,散列函数需要仔细地选择。
????????一种选择方法是把字符串中字符的ASCII码值加起来。在图5-2中,我们声明类型Index,它是散列函数的返回值类型。图5-3实现该想法并用典型的C方式通过将字符逐个相加来处理整个字符串。
typedef unsigned int Index;Index Hash(const char *Key, int TableSize)
{
unsigned int HashVal = 0;
while (*Key != '\0')
HashVal += *Key++;
return HashVal % TableSize;
}????????图5-3中描述的散列函数实现起来简单而且能够很快地算出答案。不过,如果表很大,
则函数将不会很好地分配关键字。例如,设TableSize=10007(10007?是素数),并设所
有的关键字至多8个字符长。由于char型量的值最多是127,因此散列函数只能假设值在
0和1016之间,其中1016=127×8。显然这不是一种均匀的分配。?
????????另一个散列函数由图5-4表示。这个散列函数假设Key至少有两个字符外加NULL结束符。值27表示英文字母表的字母个数外加一个空格,而。该函数只考察前
三个字符,但是,假如它们是随机的,而表的大小像前面那样还是10007,那么我们就会得到一个合理的均衡分配。可不巧的是,英文不是随机的。虽然3个字符(忽略空格)有种可能的组合,但查验词汇量足够大的联机词典却揭示:3个字母的不同组合数实际只有2851种。即使这些组合没有冲突,也不过只有表的28%被真正散列到。因此,虽然很容易计算,但是当散列表足够大的时候这个函数还是不合适的。
Index Hash(const char *Key, int TableSize)
{
return (Key[0] + 27 * Key[1] + 729 * Key[2]) % TableSize;
}????????图5-5列出了散列函数的第3种尝试。这个散列函数涉及关键字中的所有字符,并且一
般可以分布得很好(它计算,并将结果限制在适当的范围内)。程序根据Horner法则计算一个(32的)多项式函数。例如,计算
的另一种方式是借助于公式
;进行。Horner法则将其扩展到用于
次多项式。
????????我们之所以用32代替27,是因为用32作乘法不是真的去乘,而是移动二进制的5位。为了加速,在程序第2行的加法可以用按位异或来代替。
????????图5-5所描述的散列函数就表的分布而言未必是最好的,但是确实具有极其简单的优点(如果允许溢出,那么速度也很快)。如果关键字特别长,那么该散列函数计算起来将会花费过多的时间,不仅如此,前面的字符还会左移出最终的结果。在这种情况下,通常的做法是不使用所有的字符。此时关键字的长度和性质将影响选择。例如,关键字可能是完整的街道地址,散列函数可以包括街道地址的几个字符,也许是城市名和邮政区码的几个字符。有些程序设计人员通过只使用奇数位置上的字符来实现他们的散列函数,这里有这么一层想法:用计算散列函数节省下的时间来补偿由此产生的对均匀分布的函数的轻微干扰。
????????剩下的主要编程细节是解决冲突的消除问题。如果当一个元素被插入处另一个元素已经存在(散列值相同),那么就产生一个冲突,这个冲突需要消除。解决这种冲突的方法有几种,我们将讨论其中最简单的两种:分离链接法和开放定址法。
5.3 分离链接法
????????解决冲突的第一种方法通常叫作分离链接法(separate?chaining),其做法是将散列到同一个值的所有元素保留在一个表中。为方便起见,这些表都有表头,因此,表的实现与第3章中的实现方法相同。如果空间很紧,则更可取的方法是避免使用这些表头。本节假设关键字是前10个完全平方数并设散列函数就是。(表的大小不是素数,用在这里是为了简单起见。)图5-6做出更清晰的解释。

????????为执行Find,我们使用散列函数来确定究竟考察哪个表。此时我们以通常的方式遍历该表并返回所找到的被查找项所在位置。为执行Insert,我们遍历一个相应的表以检查该元素是否已经处在适当的位置(如果要插入重复元,那么通常要留出一个额外的域,这个域当重复元出现时增1)。如果这个元素是个新的元素,那么或者插入到表的前端,或者插入到表的末尾,哪个容易就执行哪个。当编写程序的时候这是最容易寻址的一种。有时将新元素插入到表的前端不仅因为方便,而且还因为新近插入的元素最有可能最先被访问。
????????实现分离链接法所需要的类型声明在图5-7中示出。图中的ListNode结构与第3章中的链表声明相同。图中的散列表结构包括一个链表数组(以及数组中的链表的个数),它们在散列表结构初始化时动态分配空间。此处的HashTable类型就是指向该结构的指针类型。
????????注意,TheList域实际上是一个指向指向ListNode结构的指针的指针。如果不使用这些typedef,那可能会相当混乱。
#ifndef _HashSep_H
struct ListNode;
typedef struct ListNode *Position;
struct HashTbl;
typedef struct HashTbl *HashTable;
HashTable InitializeTable(int TableSize);
void DestroyTable(HashTable H);
Position Find(ElementType Key, HashTable H);
void Insert(ElementType Key, HashTable H);
ElementType Retrieve(Position P);
#endif
struct ListNode
{
ElementType Element;
Position Next;
};
typedef Position List;
struct HashTbl
{
int TableSize;
List *TheLists;
};????????图5-8列出初始化函数,它用到与栈的数组实现中相同的想法。第4~6行给一个散列表结构分配空间。如果空间允许,则H将指向一个结构,该结构包含一个整数和指向一个表的指针。第7行设置表的大小为一素数,而第8~10行则试图指定List的一个数组。由于List被定义为一个指针,因此结果为指针的数组。
????????假如List的实现不用表头,那么我们就可以到此为止了。但是我们使用了表头,因此必须给每个表分配一个表头并设置它的Next域为NULL。这由第11~15行实现。当然,第12~15行可以用语句
????????H->TheLists[i]=MakeEmpty?();
代替。虽然我们没有选择使用这条语句,但是因为该例中它胜过使程序尽可能自包含,所以它当然值得考虑。这个程序的一个低效之处在于第12行上的malloc执行了H->TableSize次。这可以通过在循环出现之前调用一次malloc操作
????????H->TheLists=malloc(H->TableSize*sizeof(struct?ListNode));
代替第12行来避免。第16行返回H。
????????对Find(Key,H)的调用将返回一个指针,该指针指向包含Key的那个单元。实现它的程序在图5-9中示出。注意,第2~5行等同于第3章中给出的执行Find的程序。因此,第3章中表示ADT的实现方法可以用到这里。记住,如果ElementType是一个字符串,那么比较和赋值必须相应地使用strcmp和strcpy来进行。
HashTable InitializeTable(int TableSize)
{
HashTable H;
int i;
if (TableSize < MinTableSize)
{
Error("Table size too small");
return NULL;
}
H = malloc(sizeof(struct HashTbl));
if (H == NULL)
FatalError("Out of space!!!");
H->TableSize = NextPrime(TableSize);
H->TheLists = malloc(sizeof(List) * H->TableSize);
if (H->TheLists == NULL)
FatalError("Out of space!!!");
for (i = 0; i < H->TableSize; i++)
{
H->TheLists[i] = malloc(sizeof(struct ListNode));
if (H->TheLists[i] == NULL)
FatalError("Out of space!!!");
else
H->TheLists[i]->Next = NULL;
}
return H;
}Position Find(ElementType Key, HashTable H)
{
Position P;
List L;
L = H->TheLists[Hash(Key, H->TableSize)];
P = L->Next;
while (P != NULL && P->Element != Key)
P = P->Next;
return P;
}void Insert(ElementType Key, HashTable H)
{
Position Pos, NewCell;
List L;
Pos = Find(Key, H);
if (Pos == NULL)
{
NewCell = malloc(sizeof(struct ListNode));
if (NewCell == NULL)
FatalError("Out of space!!!");
else
{
L = H->TheLists[Hash(Key, H->TableSize)];
NewCell->Next = L->Next;
NewCell->Element = Key;
L->Next =NewCell;
}
}
}????????下一个是插入例程。如果要插入的项已经存在,那么我们就什么也不做;否则我们把
它放到表的前端(见图5-10)。该元素可以放在表的任何地方,此处这样做是最方便的。注意,插入到表的前端的程序基本上等同于第3章中使用链表实现Push的程序。如果第3章中的那些ADT都已经仔细地实现了,那么它们就可以用到这里。
????????图5-10中的插入例程写得多少有些不好,因为它计算了两次散列函数。多余的计算总是不好的,因此,如果这些散列例程真的构成程序运行时间的重要部分,那么这个程序就应该重写。
????????删除例程是链表中的删除操作的直接实现,因此我们不在这里赘述。如果在散列的诸
例程中不包括删除操作,那么最好不要使用表头,因为使用表头不仅不能简化问题而且还要浪费大量的空间。
????????除链表外,任何的方案都有可能用来解决冲突现象?一棵二叉查找树甚至另外一个散列表均可胜任,但是我们期望如果表大,同时散列函数好,那么所有的表就应该短,这样就不至于进行任何复杂的尝试了。
????????我们定义散列表的装填因子(load?factor)为散列表中的元素个数与散列表大小的比值。在上面的例子中,
。表的平均长度为
。执行一次查找所需要的工作是计算散列函数值所需要的常数时间加上遍历表所用的时间。在一次不成功的查找中,遍历的链接数平均为
(不包括最后的NULL链接)。成功的查找则需要遍历大约
个链接;它保证必然会遍历一个链接(因为查找是成功的),而我们也期望沿着一个表中途就能找到匹配的元素。这就指出,表的大小实际上并不重要,而装填因子才是重要的。分离链接散列的一般法则是使得表的大小尽量与预料的元素个数差不多(换句话说,让
)。正如前面提到的,使表的大小是素数以保证一个好的分布,这也是一个好的想法。
5.4 开放定址法
????????分离链接散列算法的缺点是需要指针,由于给新单元分配地址需要时间,因此这就导致算法的速度多少有些减慢,同时算法实际上还要求实现另一种数据结构。除使用链表解决冲突外,开放定址散列法(open?addressing?hashing)是另外一种用链表解决冲突的方法。在开放定址散列算法系统中,如果有冲突发生,那么就要尝试选择另外的单元,直到找出空的单元为止。更一般地,单元相继试选,其中
,且
。函数
是冲突解决方法。因为所有的数据都要置入表内,所以开放定址散列法所需要的表要比分离链接散列用的表大。一般说来,对开放定址散列算法来说,装填因子应该低于
。现在我们就来考察三个通常的冲突解决方法。
5.4.1 线性探测法
????????在线性探测法中,函数是
的线性函数,典型情形是
。这相当于逐个探测每个
单元(必要时可以绕回)以查找出一个空单元。图5-11显示使用与前面相同的散列函数将诸关
键字插入一个散列表的情况,而此时的冲突解决方法就是
。

????????第一个冲突在插入关键字49时产生——它被放入下一个空闲地址,即地址0,该地址是开放的。关键字58依次和18、89、49发生冲突,试选三次之后才找到一个空单元。对69的冲突用类似的方法处理。只要表足够大,总能够找到一个自由单元,但是如此花费的时间是相当多的。更糟的是,即使表相对较空,这样占据的单元也会开始形成一些区块,其结果称为一次聚集(primary?clustering),于是,散列到区块中的任何关键字都需要多次试选单元才能解决冲突,然后该关键字被添加到相应的区块中。
????????虽然我们不在这里进行具体计算,但是可以证明,使用线性探测的预期探测次数对于插入和不成功的查找来说大约为,而对于成功的查找来说则是
。一些相关的计算多少有些复杂。从程序中容易看出,插入和不成功查找需要相同次数的探测。略加思考不难得出,成功查找应该比不成功查找平均花费较少的时间。?
????????如果聚集不算是问题,那么对应的公式就不难得到。我们假设有一个很大的表,并设每次探测都与前面的探测无关。对于随机冲突解决方法而言,这些假设是成立的,并且当不是非常接近于1时也是合理的。首先,我们导出在一次不成功查找中探测的期望次数,而这正是直到我们找到一个空单元的探测的期望次数。由于空单元所占的份额为
,因此我们预计要探测的单元数是
。一次成功查找的探测次数等于该特定元素插入时所需要的探测次数。当一个元素被插入时,可以看成是一次不成功查找的结果。因此,我们可以使用一次不成功查找的开销来计算一次成功查找的平均开销。
????????需要指出,在0到当前值之间变化,因此早期的插入操作开销较少,从而降低平均开销。例如,在上面的表中,
,访问18的开销是在18被插入时确定的,此时
。由于18是插入到一个相对空的表中,因此对它的访问应该比新近插入的元素(比如69)的访问更容易。我们可以通过使用积分计算插入时间平均值的方法来估计平均值,如此得到
这些公式显然优于线性探测相应的公式。聚集不仅是理论上的问题,而且实际上也发生在具体的实现中。图5-12把线性探测的性能(虚线)与对更随机冲突解决方法中期望的性能作了比较。成功的查找用S标示,不成功查找和插入分别用U和I标记。

如果,那么上面的公式指出在线性探测中一次插入预计探测8.5次。如果
,则预计探测50次,这是不合理的。假如聚集不是问题,那么这可与相应装填因子的4次和10次探测相比。从这些公式看到,如果超过一半的表被填满的话,那么线性探测就不是个好办法。然而,如果
,那么插入操作平均只需要探测2.5次,并且对于成功的查找平均只需要探测1.5次。
5.4.2 平方探测法
????????平方探测是消除线性探测中一次聚集问题的冲突解决方法。平方探测就是冲突函数为二次函数的探测方法。流行的选择是,图5-13显示了使用该冲突函数所得到的与前面线性探测例子相同的开放定址散列表。

????????当49与89冲突时,其下一个位置为下一个单元,该单元是空的,因此49就被放在那里。此后,58在位置8处产生冲突,其后相邻的单元经探测得知发生了另外的冲突。下一个探测的单元在距位置8为2^2=4远处,这个单元是个空单元。因此,关键字58就放在单元2处。对于关键字69,处理的过程也一样。
????????对于线性探测,让元素几乎填满散列表并不是个好主意,因为此时表的性能会降低。对于平方探测情况甚至更糟:一旦表被填满超过一半,当表的大小不是素数时甚至在表被填满一半之前,就不能保证一次找到一个空单元了。这是因为最多有一半的表可以用作解决冲突的备选位置。
????????我们现在就来证明,如果表有一半是空的,并且表的大小是素数,那么我们保证总能够插入一个新的元素。
????????定理5.1?如果使用平方探测,且表的大小是素数,那么当表至少有一半是空的时候,总能够插入一个新的元素。
????????证明:令表的大小Tablesize是一个大于3的(奇)素数。我们证明,前[Tablesize/2]个备选位置是互异的。和
是这些位置中的两个,其中
,
。为推出矛盾,假设这两个位置相同,但
,于是
由于Tablesize是素数,因此,要么等于
,要么
等于
。既然
和
是互异的,那么第一个选择是不可能的。但
,
,因此第二个选择也是不可能的。从而,前
个备选位置是互异的。由于要插入的元素(若无任何冲突发生)也可以放到经散列得到的单元,因此任何元素都有
个可能的位置。如果最多有
个位置可以使用,那么空单元总能够找到。
????????哪怕表有比一半多一个的位置被填满,那么插入都有可能失败(虽然这是非常难以见到的)。把它记住很重要。另外,表的大小是素数也非常重要。如果表的大小不是素数,则备选单元的个数可能会锐减。例如,若表的大小是16,那么备选单元只能在距散列值1、4或9距离处。
????????在开放定址散列表中,标准的删除操作不能施行,因为相应的单元可能已经引起过冲突,元素绕过它存在了别处。例如,如果我们删除89,那么实际上所有其他的Find例程都将不能正确运行。因此,开放定址散列表需要懒惰删除,虽然在这种情况下并不存在真正意义上的懒惰。
????????实现开放定址散列方法所需要的类型声明在图5-14中表示。这里,我们不用链表数组,而是使用散列表项单元的数组,与在分离链接散列中一样,这些单元也是动态分配地址的。该表的初始化(图5-15)由分配空间(第1~10行)及其后将每个单元的Info域设置为Empty组成。
typedef unsigned int Index;
typedef Index Position;
struct HashTbl;
typedef struct HashTbl *HashTable;
HashTable InitializeTable(int TableSize);
void DestroyTable(HashTable H);
Position Find(ElementType Key, HashTable H);
void Insert(ElementType Key, HashTable H);
ElementType Retrieve(Position P, HashTable H);
HashTable Rehash(HashTable H);
#endif
enum KindOfEntry {Legitimate, Empty, Deleted};
struct HashEntry
{
ElementType Element;
enum KindOfEntry Info;
};
typedef struct HashEntry Cell;
struct HashTbl
{
int TableSize;
Cell *TheCells;
};HashTable InitializeTable(int TableSize)
{
HashTable H;
int i;
if (TableSize < MinTableSize)
{
Error("Table size too small");
return NULL;
}
H = malloc(sizeof(struct HashTbl));
if (H == NULL)
FatalError("Out of space!!!");
H->TableSize = NextPrime(TableSize);
H->TheCells = malloc(sizeof(Cell) * H->TableSize);
if (H->TheCells == NULL)
FatalError("Out of space!!!");
for (i = 0; i < H->TableSize; i++)
H->TheCells[i].Info = Empty;
return H;
}????????如同分离链接散列法一样,Find(Key,H)将返回key在散列表中的位置。如果Key不出现,那么Find将返回最后的单元。该单元就是当需要时,Key将被插入的地方。此外,因为被标记了Empty,所以表达Find失败很容易。为了方便起见,我们假设散列表的大小至少为表中元素个数的两倍,因此平方探测方法总能够实现。否则,我们就要在第4行前测试i(CollisionNum)。在图5-16的实现中,标记为删除的那些元素被认为还在表内。这可能引起一些问题,因为该表可能提前过满。我们现在就来讨论它。?
Position Find(ElementType Key, HashTable H)
{
Position CurrentPos;
int CollisionNum;
CollisionNum = 0;
CurrentPos = Hash(Key, H->TableSize);
while (H->TheCells[CurrentPos].Info != Empty && H->TheCells[CurrentPos].Element != Key)
{
CurrentPos += 2 * ++CollisionNum - 1;
if (CurrentPos >= H->TableSize)
CurrentPos -= H->TableSize;
}
return CurrentPos;
}????????第4~6行为进行平方探测的快速方法。由平方解决函数的定义可知,,因此,下一个要探测的单元可以用乘以2(实际上就是进行一位二进制移位)并减1来确定。如果新的定位越过数组,那么可以通过减去TableSize把它拉回到数组范围内。这比通常的方法要快,因为它避免了看似需要的乘法和除法。注意一条重要的警告:第3行的测试顺序很重要,切勿改变它!
void Insert(ElementType Key, HashTable H)
{
Position Pos;
Pos = Find(Key, H);
if (H->TableSize[Pos].Info != Legitimate)
{
H->TheCells[Pos].Info = Legitimate;
H->TheCells[Pos].Element = Key;
}
}????????最后的例程是插入。正如分离链接散列方法那样,若Key已经存在,则我们就什么也不做。其他工作只是简单的修改。否则,我们就把要插入的元素放在Find例程指出的地方,如图5-17所示。
????????虽然平方探测排除了一次聚集,但是散列到同一位置上的那些元素将探测相同的备选单元。这叫作二次聚集(secondaryclustering)。二次聚集是理论上的一个小缺憾。模拟结果指出,对每次查找,它一般要引起另外的少于一半的探测。下面的技术将会排除这个缺憾,不过这要花费另外的一些乘法和除法形销。
5.4.3 双散列
????????我们将要考察的最后一个冲突解决方法是双散列(double?hashing)。对于双散列,一种流行的选择是。这个公式是说,我们将第二个散列函数应用到
并在距离
等处探测。
选择得不好将会是灾难性的。例如,若把99插入到前面例子的输入中,则通常的选择
将不起作用。因此,函数一定不要算得0值。另外,保证所有单的元都能被探测到(在下面的例子中这是不可能的,因为表的大小不是素数)也是很重要的。诸如
这样的函数将起到良好的作用,其中R为小于TableSize的素数。如果我们选择R=7,图5-18则显示?164插入与前面相同的关键字的结果。
????????第一个冲突发生在插入49的时候。,故49被插入到位置6。
,于是58被插入到位置3。最后,69产生冲突,从而被插入到距离为
的地方。如果我们试图将60插入到位置0处,那么就会产生一个冲突。由于
,因此我们尝试位置3、6、9,然后是2,直到找出一个空的单元。一般是有可能发现某个坏情形的,不过这里没有太多这样的情形。
????????前面已经提到,上面的散列表实例的大小不是素数。我们这么做是为了计算散列函数时方便,但是,有必要了解在使用双散列时为什么保证表的大小为素数是重要的。如果想要把23插入到表中,那么它就会与58发生冲突。由于,且该表大小是10,因此我们只有一个备选位置,而这个位置已经使用了。因此,如果表的大小不是素数,那么备选单元就有可能提前用完。然而,如果双散列正确实现,则模拟表明,预期的探测次数几乎和随机冲突解决方法的情形相同。这使得双散列理论上很有吸引力。不过,平方探测不需要使用第二个散列函数,从而在实践中可能更简单并且更快。

5.5 再散列
????????对于使用平方探测的开放定址散列法,如果表的元素填得太满,那么操作的运行时间将开始消耗过长,且Insert操作可能失败。这可能发生在有太多的移动和插入混合的场合。此时,一种解决方法是建立另外一个大约两倍大的表(而且使用一个相关的新散列函数),扫描整个原始散列表,计算每个(未删除的)元素的新散列值并将其插入到新表中。
????????例如,设将元素13、15、24和6插入到大小为7的开放定址散列表中。散列函数是。假设使用线性探测方法解决冲突问题。插入结果得到的散列表如图5-19所示。
????????如果将23插入表中,那么图5-20中插入后的表将有超过70%的单元是满的。因为表填得过满,所以我们建立一个新的表。该表大小之所以为17,是因为17是原表大小两倍后的第一个素数。新的散列函数为。扫描原来的表,并将元素6、15、23、24以及13插入到新表中。最后得到的表见图5-21。


????????整个操作就叫作再散列(rehashing)。显然这是一种非常昂贵的操作,其运行时间为,因为有
个元素要再散列而表的大小约为
,不过,由于不是经常发生,因此实际效果根本没有这么差。特别是,在最后的再散列之前必然已经存在
次Insert,当然添加到每个插入上的花费基本上是一个常数开销。如果这种数据结构是程序的一部分,那么其效果是不显著的。另一方面,如果再散列作为交互系统的一部分运行,那么其插入引起再散列的不幸的用户将会感到速度减慢。
????????再散列可以用平方探测以多种方法实现。一种做法是只要表填满一半就再散列。另一种极端的方法是只有当插入失败时才再散列。第三种方法是途中(middle-of-the-road)策略:当表到达某一个装填因子时进行再散列。由于随着装填因子的增加,表的性能的确有下降,因此,以好的截止手段实现的第三种策略,可能是最好的策略。
????????再散列使程序员再也不用担心表的大小,这一点很重要,因为在复杂的程序中散列表不能够做得任意大。后面的练习让你考察再散列与懒惰删除联合使用的情况。再散列还可以用在其他的数据结构中。例如,如果第3章队列数据结构变满时,那么我们可以声明一个双倍大小的数组,并将每一个成员拷贝过来,同时释放原来的队列。
HashTable Rehash(HashTable H)
{
int i, OldSize;
Cell *OldCells;
OldCells = H->TheCells;
OldSize = H->TableSize;
H = InitializeTable(2 * OldSize);
for (i = 0; i < OldSize; i++)
if (OldCells[i].Info == Legitimate)
Insert(OldCells[i].Element, H);
free(OldCells);
return H;
}????????如图5-22所示,再散列的实现很简单。
5.6 可扩散列
????????本章最后的论题处理数据量太大以至于装不进主存的情况。正如我们在第4章看到的,此时主要考虑的是检索数据所需的磁盘存取次数。
????????与前面一样,我们假设在任意时刻都有个记录要存储,
的值随时间而变化。此外,最多可把
个记录放入一个磁盘区块。本节将设
。
????????如果使用开放定址散列法或分离链接散列法,那么主要的问题在于,在一次Find操作期间,冲突可能引起多个区块被考察,甚至对于理想分布的散列表也在所难免。不仅如此,当表变得过满的时候,必须执行代价巨大的再散列这一步,它需要次磁盘访问。
????????一种聪明的选择叫作可扩散列(extendible?hashing),它允许用两次磁盘访问执行一次Find。插入操作也需要很少的磁盘访问。
????????回忆第4章,B树具有深度。随着
的增加,B树的深度降低。理论上我们可以选择使得B树的深度为1的
。此时,在第一次以后的任何Find都将花费一次磁盘访问,因为据推测根节点可能存在主存中。这种方法的问题在于分支系数(branching?factor)太高,以至于为了确定数据在哪片树叶上要进行大量的处理工作。如果运行这一步的时间可以减缩,那么我们就将有一个实际的方案。这正是可扩散列使用的策略。
????????现在假设我们的数据由几个6位整数组成。图5-23显示这些数据的可扩散列格式。“树”的根含有4个指针,它们由这些数据的前两位确定。每片树叶有最多个元素。碰巧这里每片树叶中数据的前两位都是相同的,这由圆括号内的数指出。为了更正式,用
代表根所使用的位数,有时称其为目录(directory)。于是,目录中的项数为
。
为树叶
所有元素共有的最高位的位数。
将依赖于特定的树叶,因此
。
????????设欲插入关键字100100。它将进入第三片树叶,但是第三片树叶已经满了,没有空间存放它。因此我们将这片树叶分裂成两片树叶,它们由前三位确定。这需要将目录的大小增加到3。这些变化如图5-24所示。

????????注意,所有未被分裂的树叶现在各由两个相邻目录项所指。因此,虽然重写整个目录,
但是其他树叶都没有被实际访问。
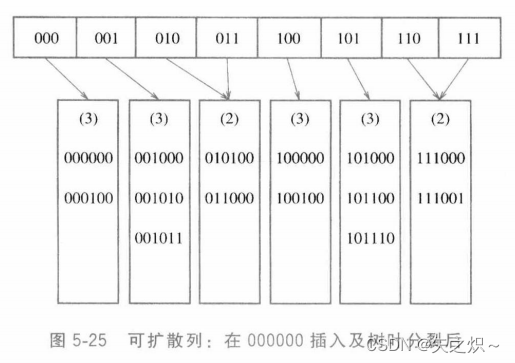
????????如果现在插入关键字000000,那么第一片树叶就要被分裂,生成的两片树叶。由于
,故在目录中所做的唯一变化是000和001指针的更新,见图5-25。
????????这个非常简单的方法提供了对大型数据库Insert操作和Find操作的快速存取时间。这里,还有一些重要细节我们尚未考虑。
????????首先,有可能当一片树叶的元素有多于个前导位相同时需要多个目录分裂。例如,从原先的例子开始,
,如果插入?111010、111011,并在最后插入111100,那么目录大小必须增加到4以区分五个关键字。这是一个容易考虑到的细节,但是千万不要忘记它。其次,存在重复关键字(duplicate?key)的可能性;若存在多于
个重复关键字,则该算法根本无效。此时,需要做出某些其他的安排。
????????这些可能性指出,这些位完全随机是相当重要的,这可以通过把关键字散列到合理长的整数(由此得名)来完成。
????????最后,我们介绍可扩散列的某些性能,这些性能是经过非常困难的分析后得到的。这?170些结果基于合理的假设:位模式(bit?pattern)是均匀分布的。
????????树叶的期望个数为。因此,平均树叶满的程度为
。这和B树是一样的,其实这完全不奇怪,因为对于两种数据结构,当添加第(
)项时,一些新的节点就建立起来了。
????????更惊奇的结果是,目录的期望大小(换句话说即)为
。如果
很小,那么目录可能过大。在这种情况下,我们可以让树叶包含指向记录的指针而不是实际的记录,这样可以增加
的值。为了维持更小的目录,可以为每个Find操作添加第二个磁盘访问。如果目录太大装不进主存,那么第二个磁盘访问怎么说也还是需要的。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!